Wheat and chessboard problem
|
Read other articles:

Artikel ini bukan mengenai No Matter How I Look at It, It's You Guys' Fault I'm Not Popular!. Hey, I'm PopularGambar sampul manga volume pertama私がモテてどうすんだ(Watashi ga Motete Dōsunda)GenreKomedi romantis,[1] Harem terbalik[2] MangaPengarangJunkoPenerbitKodanshaPenerbit bahasa InggrisNA Crunchyroll (daring)Kodansha ComicsPenerbit bahasa IndonesiaM&C!MajalahBessatsu FriendDemografiShōjoTerbit11 Oktober 2013 – 13 Februari 2018Volume14 Drama audioRilis13 ...

Pengadilan Tinggi Agama BanjarmasinPTA BanjarmasinGambaran umumLingkungan peradilanPeradilan AgamaTingkatBandingYurisdiksiProvinsi Kalimantan SelatanPengajuan kasasi/PK keMahkamah Agung Republik IndonesiaJumlah hakim17 Hakim TinggiKetuaDrs. H. Helmy Thohir, M.H.AlamatLokasiJl. Bina Praja Timur Kompleks Perkantoran Provinsi Kalimantan Selatan, Banjarbaru, Kalimantan Selatan, Kota Banjarbaru, Kalimantan Selatan, IndonesiaTelp./Faks.Telp. 0511-3252319 , Fax. 0511-3253742Situs webSitus Resmi...

Daydream World TourTur oleh Mariah CareyDaydreamMulai7 Maret 1996 (1996-03-07)Berakhir23 Juni 1996 (1996-06-23)Putaran2Penampilan3 di Asia4 di EropaTotal 7Kronologi konser Mariah Carey Music Box Tour(1993) Daydream World Tour(1996) Butterfly World Tour(1998) Daydream World Tour adalah tur konser oleh artis rekaman asal Amerika, Mariah Carey dalam mempromosikan album platinum miliknya, Daydream. Tur dimulai pada tanggal 7 Maret 1996 di Tokyo, Jepang, dan berakhir di London, Inggris p...

RinascitaStato Italia LinguaItaliano Periodicitàmensile (1944-1962) settimanale (dal 1962) GenereSettimanale politico-culturale FondatorePalmiro Togliatti Fondazione1944 Chiusura18 febbraio 1991 SedeRoma EditoreSocietà Rinascita editoriale srl Modifica dati su Wikidata · ManualeRinascita è stata una rivista italiana, in origine un mensile politico-culturale del Partito Comunista Italiano. Fu fondata da Palmiro Togliatti nel 1944. Indice 1 Storia del periodico 2 Direttori ...

1905 novel by L. Frank Baum Queen Zixi of Ix, or The Story of the Magic Cloak First book editionAuthorL. Frank BaumIllustratorFrederick RichardsonCountryUnited StatesLanguageEnglishSeriesOz booksGenreFantasy novelSet inForest of Burzee, Noland, IxPublisherSt. NicholasThe Century Company (book)Publication dateNovember 1904 – October 1905Media typePrint (Serial) Queen Zixi of Ix, or The Story of the Magic Cloak, is a children's book written by L. Frank Baum and illustrated by Freder...

Walther WA 2000 Walther WA 2000. Jenis Senapan runduk Negara asal Jerman Barat Sejarah pemakaian Digunakan oleh Polisi Jerman[1] Sejarah produksi Tahun 1970s-1980an [1] Produsen Carl Walther GmbH [1] Diproduksi 1982-1988 [1] Jumlah produksi 176 [1] Spesifikasi Berat 6.95 kg (15.3 lb) tanpa peluru dan alat bidik optik[2] 7.35 kg (16.2 lb) dengan amunisi peluru, tanpa alat bidik optik [2] Panjang 905 mm (35.6 in) [...

تُمثّل سنترال بارك في مدينة نيويورك جزءًا من نظام بيئي ضمن بيئة حضريَّة. علم البيئة الحضرية علم البيئة الحضرية، وهي الدراسة العلمية لعلاقة الكائنات الحية مع بعضها البعض ومع محيطها في مجال المنطقة الحضرية. تُشير المنطقة الحضرية إلى البيئات التي تهيمن عليها المباني السكنية...

2012 studio album by FourplayEsprit De FourStudio album by FourplayReleasedSeptember 18, 2012 (2012-09-18)Studio Glenwood Place Studios (Burbank, California) KFP Studios (Bethlehem, Pennsylvania) Landmark Studios (Yokohama, Japan) GenreJazzLength54:56LabelHeads UpProducer Fourplay (Tracks 1-9) Bob James and Atsuko Yashima (Track 10) Fourplay chronology Let's Touch the Sky(2010) Esprit De Four(2012) Professional ratingsReview scoresSourceRatingAllmusic[1] Esprit ...

2010 video game 2010 video gameMass Effect 2Developer(s)BioWarePublisher(s)Electronic ArtsMicrosoft Game Studios[a]Director(s)Casey HudsonProducer(s)Jesse HoustonNathan PlewesDesigner(s)Preston WatamaniukProgrammer(s)David FalknerArtist(s)Derek WattsWriter(s)Mac WaltersDrew KarpyshynComposer(s)Jack WallJimmy HinsonSam HulickDavid KatesSeriesMass EffectEngineUnreal Engine 3Platform(s)WindowsXbox 360PlayStation 3Release January 26, 2010 Windows, Xbox 360NA: January 26, 2010AU: January 2...

Різдво в Японії Тип неофіційне святоДата 25 грудня Різдво в Японії у Вікісховищі Різдво в Японії (яп. クリスマス, від англ. Christmas) — недержавне свято в Японії, пов'язане з впливом західної культури, але для більшості японців позбавлене релігійного змісту і відоме як рома...

Lo stato del Paraguay ricoperto dai colori della bandiera arcobaleno Le persone lesbiche, gay, bisessuali e transgender (LGBT) in Paraguay possono affrontare molteplici difficoltà. Sia l'omosessualità maschile che quella femminile sono legali in Paraguay, ma le coppie dello stesso sesso e le famiglie guidate da coppie dello stesso sesso non hanno diritto ed alcuna tutela. Indice 1 Leggi sull'attività sessuale tra persone dello stesso sesso 2 Riconoscimento delle relazioni tra persone dello...

English actress (born 1945) Francesca AnnisAnnis in trailer for Flipper's New Adventure (1964)Born (1945-05-14) 14 May 1945 (age 79)Kensington, London, EnglandOccupationActressYears active1959–presentPartner(s)Patrick Wiseman (1976–1997)Ralph Fiennes (1995–2006)Children3 Francesca Annis (born 14 May 1945)[1] is an English actress. She is known for television roles in Reckless (1998), Wives and Daughters (1999), Deceit (2000), and Cranford (2007). A six-time BAFTA TV Aw...

Dark & WildAlbum studio karya Bangtan BoysDirilis19 Agustus 2014Direkam2014GenreHip hop, dance-pop, R&B, K-popDurasi50:50BahasaKoreaLabelBig Hit EntertainmentProduserPdoggKronologi Bangtan Boys Skool Luv Affair(2014)Skool Luv Affair2014 Dark & Wild(2014) Wake Up(2014)Wake Up2014 Singel dalam album Dark & Wild DangerDirilis: 19 Agustus 2014 (2014-08-19) War of Hormone(호르몬 전쟁)Dirilis: 21 Oktober 2014 (2014-10-21) Dark & Wild merupakan album studio...

Railway station in Hebei, China This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shalingzi East railway station – news · newspapers · books · scholar · JSTOR (March 2010) (Learn how and when to remove this message) Shalingzi East railway station is a station of Jingbao Railway in Hebei. See also List of stations on Jingbao rai...
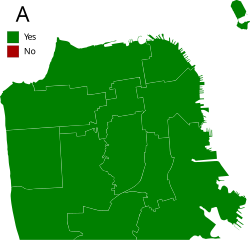
Elections in California Federal government U.S. President 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 Dem Rep 2000 Dem Rep 2004 Dem Rep 2008 Dem Rep 2012 Dem Rep 2016 Dem Rep 2020 Dem Rep 2024 Dem Rep U.S. Senate 1849 1850 1852 sp 1856 1857 sp 1860 1860 sp 1868 1872 1873 1873 sp 1878 1880 1885 1886 sp 1887 1891 1891 sp 1893 1895 sp 1897 1900 sp 1903 190...

2019 cancelled American music festival Woodstock 50Original Woodstock 50 promotional posterDatesAugust 16–18, 2019 (canceled)FoundersMichael LangWebsitewoodstock.com Woodstock 50 was a cancelled music festival originally scheduled to be held on August 16–18, 2019 at the Watkins Glen International racetrack in New York and later the Merriweather Post Pavilion in Maryland.[1] The event was intended as a commemoration of the 50th anniversary of the Woodstock Music & Art Fair, a ...

Mexican politician Hugo B. Margáin1982Secretary of Finance and Public CreditIn office13 August 1970 – 29 May 1973PresidentGustavo Díaz OrdazLuis EcheverríaPreceded byAntonio Ortiz MenaSucceeded byJosé López Portillo Personal detailsBorn(1913-02-13)13 February 1913Mexico City[1]Died11 September 1997(1997-09-11) (aged 84)Mexico[2]Political partyInstitutional Revolutionary Party (PRI)[1]SpouseMargarita Charles[1]RelationsManuel Sandoval Vallar...

2005 novel by David Bishop A Nightmare on Elm Street: Suffer the Children AuthorDavid BishopLanguageEnglishSeriesA Nightmare on Elm StreetRelease number1GenreHorrorPublisherBlack FlamePublication date26 April 2005Publication placeUnited KingdomMedia typePrint (Paperback)Pages416ISBN9781844161720OCLC61259479Followed byA Nightmare on Elm Street: Dreamspawn A Nightmare on Elm Street: Suffer the Children is a 2005 British horror novel written by David Bishop and published by Black...

Santa Clarita DietPaeseStati Uniti d'America Anno2017-2019 Formatoserie TV Generecommedia, orrore Stagioni3 Episodi30 Durata25 min (episodio) Lingua originaleinglese Rapporto16:9 CreditiIdeatoreVictor Fresco Interpreti e personaggi Drew Barrymore: Sheila Hammond Timothy Olyphant: Joel Hammond Liv Hewson: Abby Hammond Skyler Gisondo: Eric Bemis Doppiatori e personaggi Rossella Acerbo: Sheila Hammond Massimo De Ambrosis: Joel Hammond Ludovica Bebi: Abby Hammond Federico Bebi: Eric Bemis Mus...

Cet article est une ébauche concernant une commune de la Nièvre. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour vous aider. Consultez également la page d’aide ...


















