Seked
|
Read other articles:

Halaman ini berisi artikel tentang Kota dan munisipalitas. Untuk desa dengan nama yang sama, lihat Kamenica, Leposavić. Kamenica atau Dardana (bahasa Albania: Kamenicë atau Dardanë), atau Kosovska Kamenica (bahasa Serbia: Косовска Каменица), adalah kota dan munisipalitas yang berada di Distrik Gjilan, Kosovo.[a] Menurut sensus tahun 2011, kota Kamenica dihuni oleh 7.331 penduduk, sedangkan untuk keseluruhan munisipalitas sebanyak 36.085 orang. Sejarah Kamenica mempu...

Jahe cangkang Bentuk tanaman Buah Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae Upakerajaan: Trachaeophyta Divisi: Magnoliophyta Kelas: Liliopsida Ordo: Zingiberales Famili: Zingiberaceae Genus: Alpinia Spesies: Alpinia zerumbet(Pers.) B.L.Burtt & R.M.Sm.[1] Sinonim Costus zerumbet Pers. Alpinia cristata Griff. Alpinia fimbriata Gagnep. Alpinia fluvitialis Hayata Alpinia penicillata Roscoe Alpinia schumanniana Valeton Amomum nutans (Andrews) Schult. Catimbium speciosum (...
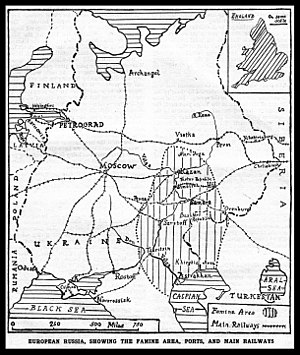
Wilayah bencana kelaparan pada musim gugur 1921. Bencana kelaparan Rusia 1921, juga dikenal dengan sebutan bencana kelaparan Povolzhye, adalah sebuah bencana kelaparan yang terjadi di Bolshevik Rusia yang dimulai pada awal musim semi 1921 dan berakhir pada 1922. Bencana kelaparan tersebut menewaskan sekitar 6 juta orang, yang utamanya berdampak pada wilayah Volga dan Sungai Ural.[1][2][3] Referensi ^ Marxist Dreams and Soviet Realities, Marxist Dreams and Soviet Realit...

American international school in Thorpe, Runnymede, Surrey, EnglandTASIS EnglandLocationThorpe, Runnymede, Surrey, TW20 8TEEnglandCoordinates51°24′29″N 0°31′34″W / 51.408°N 0.526°W / 51.408; -0.526InformationSchool typeAmerican international school(Day & boarding school)Founded1976Sister schoolTASIS SchoolsHeadmasterBryan NixonGradesPre-K — 12Enrollment646Colour(s)Blue and red MascotTASIS LionAffiliationsCISNEASCWebsitewww.tasisengland.or...

Presiding officer of the U.S. Continental Congress President of the United States in Congress AssembledSeal of the president of the CongressContinental CongressStyleMr. President (informal)The Honorable (formal)StatusPresiding officerAppointerVote within the CongressFormationSeptember 5, 1774 (1774-09-05)First holderPeyton RandolphFinal holderCyrus GriffinAbolishedNovember 2, 1788 (1788-11-02) This article is part of a series on theUnited StatesContinental Congre...

حقبة الممالك المتحاربة تاريخ الصين القديم العصر الحجري ح. 8500 – ح. 2070 ق م سلالة شيا ح. 2070 – ح. 1600 ق م سلالة شانغ ح. 1600 – ح. 1046 ق م سلالة تشو ح. 1046 – 256 ق م تشو الغربية تشو الشرقية المجتمع العبيدي الربيع والخريف الممالك المتحاربة الإمبراطوري سلا...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Uang logam 1 centavo Brasil Uang logam 1 centavo (R$0,01) adalah nilai nominal uang koin yang pertama kali dikeluarkan di Brasil pada tahun 1994. Uang logam ini memiliki nilai 1/100 di real Brasil, dan dihentikan pada tahun 2006. lbsReal Brasil (R$)Topik Casa da Moeda do Brasil • Banco Central do Brasil • Uang logam Real • Uang kertas Real Uang logam R$0,01 • R$0,05 • R$0,10 • R$0,25 • R$0,50 • R$1 Uang kertas R$1 • R$2 • R$5 • R$10 • R$20 • R$50 • R$100 Artikel be...

Malaysian state constituency Batu Maung (N37) Penang constituencyBatu Maung (olive) on PenangState constituencyLegislaturePenang State Legislative AssemblyMLA Mohamad Abdul HamidPHConstituency created2004First contested2004Last contested2023DemographicsElectors (2023)[1]47,226Area (km²)[2]21 Batu Maung is a state constituency in Penang, Malaysia, that has been represented in the Penang State Legislative Assembly since 2004. It covers the southeastern corner ...

Chemical compound Baricitinib Clinical dataTrade namesOlumiant, othersOther namesINCB28050, LY3009104AHFS/Drugs.comMonographMedlinePlusa618033License data US DailyMed: Baricitinib Pregnancycategory AU: D[1][2] Use is contraindicated Routes ofadministrationBy mouthATC codeL04AF02 (WHO) Legal statusLegal status AU: S4 (Prescription only)[4][1] CA: ℞-only[5][6] US: WARNING[3]Rx-only[7] EU:&...

Village in Hertfordshire, England Not to be confused with Welwyn Garden City. For other uses, see Welwyn (disambiguation). Human settlement in EnglandWelwynSt Mary the Virgin, WelwynWelwynLocation within HertfordshirePopulation8,425 (2011 Census)[1]OS grid referenceTL225165Civil parishWelwyn [2]DistrictWelwyn HatfieldShire countyHertfordshireRegionEastCountryEnglandSovereign stateUnited KingdomPost townWELWYNPostcode districtAL6Dialling code0...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

1900年美國總統選舉 ← 1896 1900年11月6日 1904 → 447張選舉人票獲勝需224張選舉人票投票率73.2%[1] ▼ 6.1 % 获提名人 威廉·麥金利 威廉·詹寧斯·布賴恩 政党 共和黨 民主党 家鄉州 俄亥俄州 內布拉斯加州 竞选搭档 西奧多·羅斯福 阿德萊·史蒂文森一世 选举人票 292 155 胜出州/省 28 17 民選得票 7,228,864 6,370,932 得票率 51.6% 45.5% 總統選舉結果地圖,紅色代表�...

Main Prem Ki Diwani HoonSutradaraSooraj BarjatyaProduserAjit Kumar BarjatyaKamal Kumar BarjatyaRajkumar BarjatyaSkenarioSooraj BarjatyaCeritaSooraj BarjatyaSubodh GhoshPemeranHrithik RoshanAbhishek BachchanKareena KapoorPenata musikAnu MalikSinematograferRajan KinagiPenyuntingMukhtar AhmedDistributorRajshri ProductionsTanggal rilis 26 Juni 2003 (2003-06-26) Durasi197 menitNegaraIndiaBahasaHindi Main Prem Ki Diwani Hoon adalah sebuah film drama romansa komedi Hindi India tahun 2003 ...
Crime of betraying one's country For other uses, see Treason (disambiguation), High Treason (disambiguation), and Traitor (disambiguation). Traitor redirects here. For the act itself, see Betrayal. A 17th-century illustration of the leaders of the Gunpowder Plot, a failed assassination attempt against James I of England.Criminal law Elements Actus reus Mens rea Causation Concurrence Scope of criminal liability Accessory Accomplice Complicity Corporate Principal Vicarious Severity of offense F...

Questa voce sull'argomento ciclisti polacchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Łukasz OwsianNazionalità Polonia Altezza181 cm Peso66 kg Ciclismo SpecialitàStrada Squadra Arkéa CarrieraGiovanili 2008-2011MG.K Vis-Norda Whistle Squadre di club 2012-2018 CCC Polkowice2019 CCC Team2020- Arkéa Nazionale 2016- Polonia Statistiche aggiornate al 16 marzo 2024 Modifica dati su Wikidata · Manuale Łukasz Ows...

Chabad House in Bangkok. The history of Jews in Thailand began in the 18th century with the arrival of Baghdadi Jewish families and Jewish peoples from Europe during the Napoleonic era (1799–1815). History During World War II, Thailand was a part of the Axis powers,[1] however it has had friendly diplomatic relations with Israel since 1954.[2] The Jewish community of Thailand today is mostly made up of the Ashkenazi descendants of refugees from Russia and the Soviet Union. T...

Railway station in Tel Aviv, Israel Tel Aviv HaHaganaתחנת תל אביב ההגנהIsrael RailwaysGeneral informationLocation32 HaHagana Way, Tel AvivCoordinates32°03′15″N 34°47′05″E / 32.05417°N 34.78472°E / 32.05417; 34.78472Line(s)Jaffa–Jerusalem railwayAyalon railwayPlatforms5Tracks5ConstructionAccessibleYesHistoryOpened22 June 2002; 22 years ago (2002-06-22)Electrified21 December 2019; 4 years ago (2019-12-21)Pa...

German footballer (born 1989) For other people named Thomas Müller, see Thomas Müller (disambiguation). Thomas Müller Müller with Bayern Munich in 2022Personal informationFull name Thomas Müller[1]Date of birth (1989-09-13) 13 September 1989 (age 34)[2]Place of birth Weilheim in Oberbayern, West GermanyHeight 1.85 m (6 ft 1 in)[3]Position(s) Forwardattacking midfielderTeam informationCurrent team Bayern MunichNumber 25Youth career1993–2000 TS...

List of events ← 1764 1763 1762 1761 1760 1765 in Wales → 1766 1767 1768 1769 1770 Centuries: 16th 17th 18th 19th 20th Decades: 1740s 1750s 1760s 1770s 1780s See also:List of years in WalesTimeline of Welsh history 1765 in Great Britain Scotland Elsewhere Events from the year 1765 in Wales. Incumbents Lord Lieutenant of Anglesey – Sir Nicholas Bayly, 2nd Baronet[1][2][3][4] Lord Lieutenant of Brecknockshire and Lord Lieutenant of Monmouthshire �...



