Read other articles:

Peta dunia berdasarkan angka kelahiran oleh CIA Dalam demografi, istilah angka kelahiran kasar atau tingkat kelahiran kasar (bahasa Inggris: crude birth rate) dari suatu populasi adalah jumlah kelahiran per 1.000 orang tiap tahun. Secara matematika, angka ini bisa dihitung dengan rumus CBR = n/((p)(1000)); di mana n adalah jumlah kelahiran pada tahun tersebut dan p adalah jumlah populasi saat penghitungan. Hasil penghitungan ini digabungkan dengan tingkat kematian untuk menghasilkan angka tin...

This article is about the 2006 American reality series that aired on ESPN. For the 1997 British children's series that aired on ITV, see Knight School (British TV series). American TV series or program Knight SchoolCoach Bob KnightStarringBob KnightCountry of originUnited StatesOriginal languageEnglishNo. of episodes6ProductionRunning time40-45 minutesProduction companyRIVR MediaOriginal releaseNetworkESPNReleaseFebruary 19 (2006-02-19) –March 26, 2006 (2006-03-26) Knight Sch...

It has been suggested that Rhythm & Praise music be merged into this article. (Discuss) Proposed since February 2024. Christian rhythm and bluesStylistic originsRhythm and blues, gospelCultural origins1940s–1950s, United StatesTypical instrumentsDrum kit, bass guitar, saxophone, horns, piano, organ, electric guitar, vocals, background vocalsFusion genresHip hop/R&B, rockabilly Christian R&B (also known as gospel R&B, rhythm & praise music, and R&P) is a subgenre of r...

Camelidae Periode 45–0 jtyl PreЄ Є O S D C P T J K Pg N Eosen Tengah-Holosen Camelidae Unta berpunuk satu (Camelus dromedarius)TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoArtiodactylaSuperfamiliCameloideaFamiliCamelidae Gray, 1821 Tipe taksonomiCamelus GeneraLama Vicugna Camelus †Paracamelus †CamelopsDistribusiPersebaran anggota Camelidae di masa kini. lbs Camelidae adalah binatang berjari kuku genap, mereka diklasifikasikan dalam ordo Artiodactyla. Unta adalah spesies...

  لمعانٍ أخرى، طالع أييوس كونستانتينوس (توضيح). أييوس كونستانتينوس   تقسيم إداري البلد اليونان  [1] خصائص جغرافية إحداثيات 38°45′29″N 22°51′28″E / 38.758164°N 22.857871°E / 38.758164; 22.857871   الارتفاع 10 متر  السكان التعداد السكاني 2574 (2001)2362 (1991)2289 (resident population of Greece) (...

Jari Litmanen Informasi pribadiNama lengkap Jari Olavi LitmanenTanggal lahir 20 Februari 1971 (umur 53)Tempat lahir Hollola, FinlandiaTinggi 1,82 m (5 ft 11+1⁄2 in)Posisi bermain StrikerAttacking midfielder Second strikerInformasi klubKlub saat ini FC LahtiNomor 10Karier junior1977–1987 ReipasKarier senior*Tahun Tim Tampil (Gol) 1987–1990 1991 1992 1992–1999 1999–2001 2001–2002 2002–2004 2004 2005 2005–2007 2008 2008- Reipas HJK MyPa Ajax FC Barcelona ...

2005 animated film by Nick Park and Steve Box For the video game, see Wallace & Gromit: The Curse of the Were-Rabbit (video game). Wallace & Gromit:The Curse of the Were-RabbitBritish theatrical release posterDirected by Nick Park Steve Box Screenplay by Steve Box Nick Park Mark Burton Bob Baker Based onWallace and Gromitby Nick ParkProduced by Claire Jennings Carla Shelley Peter Lord David Sproxton Nick Park StarringPeter SallisRalph FiennesHelena Bonham CarterCinematographyDavid Ale...

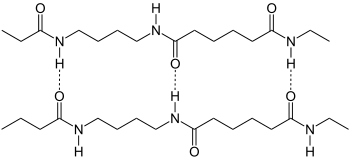
Un polyamide (PA)[1] est un polymère contenant des fonctions amide − C ( = O ) − N H − {\displaystyle \mathrm {-C(=O)-NH-} } pouvant résulter de la polycondensation entre les fonctions acide carboxylique et amine. En 1927, la société américaine Du Pont de Nemours constitue un service de recherches pour l’étude de la synthèse des polymères à longues chaînes. La direction en est confiée à Wallace Hume Carothers. Le polyamide 6/6 est découvert en 1936, la prod...

Countries and capitals of Central America Part of a series onCentral America Countries Belize Costa Rica El Salvador Guatemala Honduras Nicaragua Panama Culture Central American Spanish Cuisine Mesoamerica Music Ethnic groups Ethnic groups List of indigenous peoples Visual arts by indigenous peoples Religion Anglican Church Bahá'í Faith Buddhism Roman Catholicism Sport Central American Games Central American and Caribbean Games Football Union By country Belize Costa Rica El Salvador Guatema...

PT MD Musik IndonesiaKantor pusat MD di JakartaNama dagangMD MusicJenisPerseroan terbatasIndustriMusikDidirikan6 Maret 2003; 21 tahun lalu (2003-03-06) di Jakarta, IndonesiaPendiri Dhamoo Punjabi Manoj Punjabi KantorpusatJl. Setiabudi Selatan No. 7, Jakarta Selatan, IndonesiaWilayah operasiIndonesiaTokohkunci Dhamoo Punjabi Manoj Punjabi Shania Punjabi Divisi MD Entertainment MD Pictures MD Animation Situs webmdentertainment.com PT MD Musik Indonesia (MD Music) adalah perusahaan rekaman ...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Unione Sportiva Triestina Calcio. Unione Sportiva TriestinaStagione 1967-1968Sport calcio Squadra Triestina Allenatore Enrico Radio Presidente Giorgio Guarnieri Serie C15º posto nel girone A. Maggiori presenzeCampionato: Pedroni (37) Miglior marcatoreCampionato:...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

Federal Institute of Education, Science and Technology of Minas GeraisPortuguese: Instituto Federal de Educação, Ciência e Tecnologia de Minas GeraisOther namesFederal Institute of Minas GeraisIFMGTypePolytechnic universityEstablished2010; 14 years ago (2010)LocationBelo HorizonteBambuíCongonhasFormigaGovernador ValadaresOuro PretoOuro BrancoSão João EvangelistaJoão Monlevade, Minas Gerais, BrazilCampusUrban, multiple sitesWebsitewww.ifmg.edu.br The Federal Institute...

Questa voce o sezione sull'argomento geometria non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. La trisezione di un angolo, vale a dire la costruzione di un angolo di ampiezza un terzo di un altro angolo qualsiasi dato, assieme al problema della duplicazione del cubo e a quello della quadratura del cerchio...

State park in Oregon, United States Tumalo State ParkThe Deschutes River at the parkShow map of OregonShow map of the United StatesTypePublic, stateLocationDeschutes County, OregonNearest cityBend, OregonCoordinates44°07′37″N 121°19′55″W / 44.1270619°N 121.3319784°W / 44.1270619; -121.3319784[1]Area330 acres (130 ha)Created1954Operated byOregon Parks and Recreation Department Tumalo State Park is a well-developed state park in Deschut...

歡樂無法黨歡樂無法黨标志英語名称Can't Stop This Party[1]榮譽主席柚子[註 1]歡樂總書記[註 2]邱威傑创始人邱威傑、張志祺、陳子見成立2019年11月14日 (2019-11-14)解散2021年2月19日 (2021-02-19)（1年97天）总部臺北市大安區羅斯福路二段111號8樓党员（2019年）115人[3]意識形態社会自由主义进步主义政治立場中間偏左党歌《歡樂無法黨黨歌》[4]中華民...

Head of state and commander-in-chief of Croatia President of the Republic of CroatiaPredsjednik Republike HrvatskeCoat of arms of the presidentStandard of the presidentIncumbentZoran Milanovićsince 19 February 2020Office of the President of the RepublicStyleMr President (informal)His Excellency (diplomatic)TypeHead of stateMember ofArmed Forces of CroatiaReports toCroatian ParliamentResidence36 Krajiška Street, Zagreb[1][2]SeatPredsjednički dvori, ZagrebAppointerPopula...

Elm tree in Boston, Massachusetts, US (1646–1775) For other uses, see Liberty Tree (disambiguation). The Liberty Tree in Boston, illustrated in 1825 The Liberty Tree (1646–1775) was a famous elm tree that stood in Boston, Massachusetts near Boston Common in the years before the American Revolution. In 1765, Patriots in Boston staged the first act of defiance against the British government at the tree. The tree became a rallying point for the growing resistance to the rule of Britain over ...

Disambiguazione – Se stai cercando le autorità esistenti negli altri Stati, vedi Consiglio di Stato (disambigua). Consiglio di Stato della Repubblica Popolare Cinese 中华人民共和国国务院 Zhōnghuá Rénmín Gònghéguó GuówùyuànStemma della Repubblica Popolare Cinese Stato Cina TipoBranca esecutiva del Governo centrale della Repubblica Popolare Cinese; Corpo esecutivo dell'Assemblea nazionale del popolo; Organo più alto dell'amministrazione di Stato della Repubblica Po...

Metro station in Shenzhen, China Xiangmei North香梅北Chinese nameChinese香梅北Literal meaningFragrant Blossom NorthTranscriptionsStandard MandarinHanyu PinyinXiāngméi BěiYue: CantoneseJyutpingHoeng1 Mui4 Bak1 General informationLocationFutian District, Shenzhen, GuangdongChinaOperated bySZMC (Shenzhen Metro Group)Line(s)     Line 2Platforms2 (1 island platform)Tracks2ConstructionStructure typeUndergroundAccessibleYesOther informationStation code218HistoryOpen...