Read other articles:

Geografi Filipina BenuaAsiaKawasanAsia TenggaraWilayahPeringkat ke-72300.000 km² (115.830,6 mil²)99,18% daratan0,82% perairanTitik tertinggiGunung Apo 3.776 mTitik terendahlongest river= largest lake= Filipina adalah kelompok atau gugus pulau-pulau yang berjajar di lepas pantai Indochina, membentuk batas timur laut bagi Malaysia. Kepulauan tropis ini, berbatasan dengan Laut Cina Selatan di sebelah Barat, Samudra Pasifik di sebelah Timur, Laut Sulawesi dan Laut Sulu di Selatan. Ne...

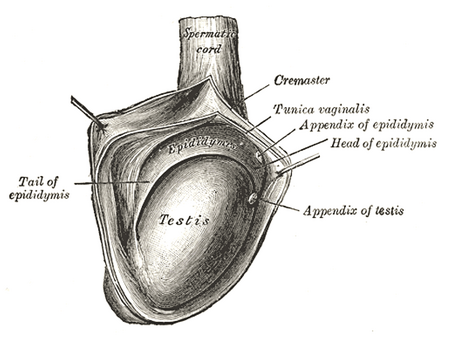
Hidrokel testisTestis kanan, terlihat dengan membuka tunica vaginalis. (Tunica vaginalis dilabeli pada kanan atas.)Informasi umumSpesialisasiUrologi Hidrokel testis adalah adanya cairan di sekitar testis (buah zakar) yang menyebabkan skrotum (kantong zakar) menjadi bengkak. Hidrokel adalah penumpukan cairan yang berlebihan di antara lapisan parietalis dan viseralis tunika vaginalis. Penyebab Prosesus vaginalis belum tertutup sempurna sehingga terjadi aliran cairan peritoneum ke prosesus vagin...

For the Twelfth Army Corps of the Union Army during the American Civil War, see XII Corps (Union Army). XII CorpsShoulder sleeve insignia of XII CorpsActive1933–45Country United StatesBranch United States ArmySizeCorpsPart ofThird United States ArmyEngagementsWorld War IICommandersNotablecommandersManton S. EddyStafford LeRoy IrwinMilitary unit U.S. Corps (1939–present) Previous Next XI Corps (United States) XIII Corps (United States) Route of march of U.S. XII Corps. The XII Co...

Steve MartinLahirStephen Glenn MartinTinggi183 cm (6 ft 0 in)Suami/istriVictoria Tennant (1986-1994)Anne Stringfield (2007 - sekarang )PenghargaanPenghargaan Aktor Terbaik NYFCC1984 All of MeSitus webwww.stevemartin.com/ Stephen Glenn Steve Martin (lahir 14 Agustus 1945) adalah komedian, penulis, produser, aktor, musikus, dan komponis asal Amerika Serikat. Biografi Awal karier Martin dilahirkan di Waco, Texas dari ayah bernama Glenn Vernon Martin dan ibu bernama Mary Lee Stewa...

5-Nitroimidazol[1] Nama Nama IUPAC (preferensi) 5-Nitro-1H-imidazol Penanda Nomor CAS 3034-38-6 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChemSpider 10637918 Y Nomor EC PubChem CID 18208 Nomor RTECS {{{value}}} UNII Y8U32AZ5O7 Y CompTox Dashboard (EPA) DTXSID9062803 InChI InChI=1S/C3H3N3O2/c7-6(8)5-2-1-4-3-5/h1-3H YKey: KUNMIWQQOPACSS-UHFFFAOYSA-N Y SMILES c1cn(cn1)[N+](=O)[O-] Sifat Rumus kimia C3H3N3O2 Massa molar 113,08 g·mol−1 &#...

Organism that ingests organic carbon for nutrition Cycle between autotrophs and heterotrophs. Autotrophs use light, carbon dioxide (CO2), and water to form oxygen and complex organic compounds, mainly through the process of photosynthesis (green arrow). Both types of organisms use such compounds via cellular respiration to both generate ATP and again form CO2 and water (two red arrows). A heterotroph (/ˈhɛtərəˌtroʊf, -ˌtrɒf/;[1][2] from Ancient Greek ἕτερ...

Lanskap Pamplona. Pamplona (bahasa Basque: Iruñea atau Iruña) merupakan kota yang terletak di sebelah utara Spanyol. Penduduknya berjumlah 191.000 jiwa (2004) dan luas wilayahnya adalah 23,55 km2. Artikel bertopik geografi atau tempat Spanyol ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

BMW Seri 4InformasiProdusenBMWModel untuk tahun2014–sekarangBodi & rangkaKelasMobil kompak eksekutif, Grand TourerBentuk kerangka2-door coupé, 2-door konvertibel, 4-door Gran CoupéKronologiPendahuluBMW Seri 3 Coupe E92 BMW Seri 4 adalah coupé kompak eksekutif yang diproduksi produsen Jerman BMW. Detail pertama Seri 4 dirilis ke publik tanggal 5 Desember 2012 untuk menggantikan coupé seri 3 dengan jajaran seri 4 yang baru untuk pembeda.[1][2] F32/F33/F36 Gen...

Cet article possède des paronymes, voir Les Tontons tringleurs et Les Tontons farceurs. Les Tontons flingueurs Affiche secondaire du film, montrant les mots d'argot utilisés et leur signification. Données clés Réalisation Georges Lautner Scénario Albert SimoninGeorges Lautner (non crédité) Acteurs principaux Lino VenturaBernard BlierJean LefebvreFrancis BlancheVenantino VenantiniRobert DalbanSabine SinjenClaude Rich Sociétés de production GaumontLes Films CoronaUltra FilmSicilia Ci...

JentakaPosterSutradaraDen Bagus AbdilahProduserYuri KimCerita Den Bagus Abdilah Yuri Kim Pemeran Yuri Kim Ayana Shahab Rezky Wiranti Dhike Stanlie Thiodorus Penata musikFernando FaustinoSinematografer Fiddy Fauzan Den Bagus Abdilah PenyuntingDen Bagus AbdilahPerusahaanproduksi Kemara Films Orijin Entertainment Tanggal rilis 16 September 2022 (2022-09-16) (Genflix) Durasi24 menitNegara IndonesiaBahasaIndonesia Jentaka adalah film cerita seru Indonesia tahun 2022 yang disutr...

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2017年12月19日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：若望保祿二世 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 �...

1991 video game2nd Super Robot WarsDeveloper(s)WinkysoftPublisher(s)BanprestoNintendo (GBA)SeriesSuper Robot WarsPlatform(s)FamicomGame BoySony PlayStationReleaseFamicomJP: December 12, 1991Game Boy (As 2nd Super Robot Wars G)JP: June 30, 1995PlayStationJP: June 10, 1999 (Complete Box)JP: December 2, 1999 (Separate release)Game Boy AdvanceJP: December 16, 2004 {Promotional only. Bundled with GC.)PlayStation NetworkJP: January 26, 2011Genre(s)Tactical role-playingMode(s)Single player 2nd Super...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

密西西比州 哥伦布城市綽號：Possum Town哥伦布位于密西西比州的位置坐标：33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里（57.8 平方公里） • 陸地21.4 平方英里（55.5 平方公里） • ...

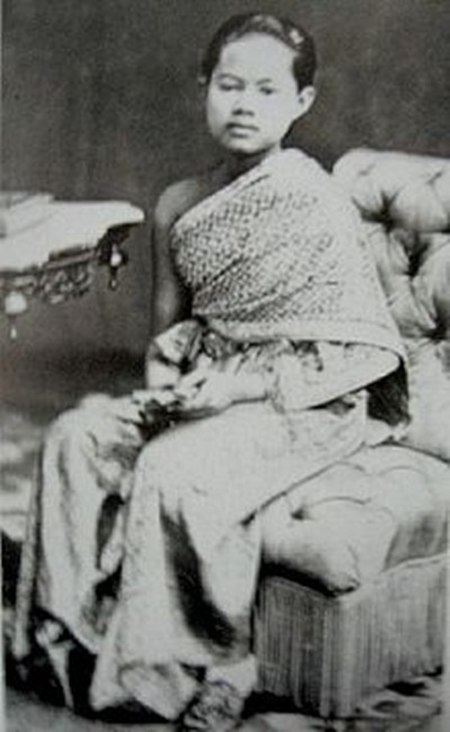
Sunandha Kumariratanaสุนันทากุมารีรัตน์Permaisuri SiamKelahiranPhra Sisriyya Phra Chao Luk Thoe Phra Ong Chao Sunandha Kumariratana(1860-11-10)10 November 1860Bangkok, SiamKematian31 Mei 1880(1880-05-31) (umur 19)Pak Kret, Nonthaburi, SiamWangsaWangsa ChakriNama lengkapSunandha Kumariratanaสุนันทากุมารีรัตน์Nama anumertaSomdet Phra Nang Chao Sunandha Kumariratana Phra Boromma RajadeviAyahMongkut (Rama IV)IbuChao Chom...

Provincial park in Ontario, Canada Not to be confused with Sandbanks Provincial Park (Newfoundland). Sandbanks Provincial ParkIUCN category II (national park)LocationSouthern Ontario, CanadaNearest cityBelleville, OntarioCoordinates43°54′N 77°16′W / 43.900°N 77.267°W / 43.900; -77.267Area1,550.87 ha (5.9879 sq mi)Established1970Governing bodyOntario Parks View of the Sandbanks in the Fall showing the dunes and foliage before the snow fa...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (February 2019) (Learn how and when to remove this message) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing...

Dominican footballer (born 1997) In this Spanish name, the first or paternal surname is Marte and the second or maternal family name is de León. Lucia León León with Tottenham Hotspur in 2018Personal informationFull name Lucía Marte de LeónDate of birth (1997-08-14) 14 August 1997 (age 26)Place of birth Madrid, SpainHeight 1.70 m (5 ft 7 in)Position(s) Right back[1]Team informationCurrent team WatfordNumber 2Youth career Madrid CFFSenior career*Years T...

Public park in Bangkok, Thailand Chatuchak ParkสวนจตุจักรTypePublic urban parkLocationChatuchak District, Bangkok, ThailandWater feature Chatuchak Park (Thai: สวนจตุจักร, RTGS: Suan Chatuchak, pronounced [sǔa̯n t͡ɕàʔ.tùʔ.t͡ɕàk]) is a public park in the southwest part of Chatuchak District, Bangkok, Thailand. It is also the name of the Chatuchak Park MRT station that lies under the park. Its name is the origin name of Chatuchak di...

Description of flat one-vertex origami In this example, the alternating sum of angles (clockwise from the bottom) is 90° − 45° + 22.5° − 22.5° + 45° − 90° + 22.5° − 22.5° = 0°. Since it adds to zero, the crease pattern may be flat-folded. Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is ...