Russell Alger Memorial Fountain

Russell Alger Memorial Fountain
The fountain in 2022
Map
42°20′13″N 83°03′00″W / 42.33689°N 83.04993°W / 42.33689; -83.04993
LocationGrand Circus Park Historic District, Detroit, Michigan, United States
DesignerDaniel Chester French (sculptor)
Henry Bacon (architect)
TypeFountain
Statue
MaterialBronze
Dedicated dateJuly 27, 1921
Dedicated toRussell A. Alger

Russell Alger Memorial Fountain is a Detroit, Michigan fountain, one of the "most successful collaborations" created by the sculptor, Daniel Chester French and architect Henry Bacon. The bronze statue was cast by the Gorham Manufacturing Company.[1] It is located in Grand Circus Park and was dedicated on July 27, 1921.

The Beaux-Arts styled bronze monument consists of a "spirited"[2] female personification of "Michigan" with one hand raised in greeting while the other holds a sword and shield. The crest of the state of Michigan is on the shield in shallow relief. There is a bas relief portrait of Alger on the granite base. Lion heads on the base serve as founts to pour water into the surrounding bowl.

Russell Alger (1836–1907) was a Civil War veteran (he enlisted as a private and ended the war as a general), politician (Governor of Michigan, U.S. Senator from Michigan, and U.S. Secretary of War), and a very successful businessman. Following Alger's death a "memorial society" of Civil War veterans convened and commissioned the work.[3]

See also

References

  1. ^ Richman, Michael, "Daniel Chester French: An American Sculptor", The Preservation Press, Washington D.C., 1976 pp. 164–170
  2. ^ Richman, Michael, "Daniel Chester French: An American Sculptor", The Preservation Press, Washington D.C., 1976 pp. 169
  3. ^ Nawrocki, Dennis Alan, with Thomas J Holleman, "Art In Detroit Public Places", Wayne State University Press, Detroit 1980 pp. 20–21

Media related to Russell Alger Memorial Fountain at Wikimedia Commons

Read other articles:

0,999...

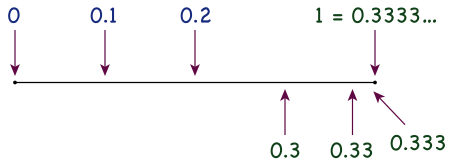
Bilangan desimal dengan angka 9 berulang tak terhingga. 0,999… dalam matematika adalah suatu bilangan desimal yang memuat angka 9 berulang tak terhingga. Juga bisa ditulis sebagai 0 , 9 ¯ {\displaystyle 0,{\bar {9}}} , 0 , 9 ˙ {\displaystyle 0,{\dot {9}}} , atau   0 , ( 9 ) {\displaystyle \ 0,(9)} . Bilangan ini merupakan sebuah bilangan real yang secara matematis memiliki nilai sama dengan 1. Dengan kata lain, 0,999… mewakili bilangan yang sama dengan angka 1. Persamaa...

 

Claudio Marchisio

Claudio Marchisio Marchisio bersama Zenit Saint Petersburg pada 2018Informasi pribadiNama lengkap Claudio Marchisio[1]Tanggal lahir 19 Januari 1986 (umur 38)[1]Tempat lahir Turin, ItaliaTinggi 180 cm (5 ft 11 in)[2]Posisi bermain GelandangKarier junior1993–2005 JuventusKarier senior*Tahun Tim Tampil (Gol)2005–2018 Juventus 294 (33)2007–2008 → Empoli (pinjaman) 26 (0)2018–2019 Zenit Saint Petersburg 9 (2)Total 329 (35)Tim nasional2007–20...

 

Dennis Ritchie

Dennis MacAlistair RitchieDennis Ritchie pada tahun 1999Lahir(1941-09-09)9 September 1941Bronxville, New York, Amerika SerikatMeninggal12 Oktober 2011(2011-10-12) (umur 70)Murray Hill, New Jersey, Amerika SerikatAlmamaterHarvard UniversityDikenal atasALTRANBBCPLCMulticsUnixPenghargaanTuring AwardNational Medal of TechnologyKarier ilmiahBidangIlmu komputerInstitusiLucent TechnologiesBell Labs Dennis MacAlistair Ritchie (9 September 1941 – 12 Oktober 2011)[1][2...

Superkonduktivitas suhu-tinggi

Superkonduktor suhu-tinggi umumnya adalah hal yang mempertunjukkan superkonduktivitas pada suhu di atas suhu nitrogen cair, atau −196 °C (77 K), karena ini merupakan suhu cryogenik yang mudah dicapai. Superkonduktor konvensional membutuhkan suhu tidak lebih dari beberapa derajat di atas nol mutlak (−273.15 °C atau −459.67 °F). Sejarah Istilah superkonduktor suhu-tinggi pertama kali digunakan untuk menunjuk ke material keramik cuprate-perovskite yang ditemukan oleh...

 

LibreOffice

LibreOffice Wahana mulai pada LibreOffice 7.2.4.1 (dirilis pada bulan Desember 2021, dijalankan di Linux dan KDE Plasma 5 dengan bundel ikon Breeze)TipePaket aplikasi perkantoran BerdasarkaOpenOffice.org Versi pertama25 Januari 2011; 13 tahun lalu (2011-01-25)Versi stabil 7.6.6 (28 Maret 2024) 24.2.2 (28 Maret 2024) GenrePaket aplikasi perkantoranLisensiGNU LGPLv3 dengan kontribusi baru berlisensi-ganda di bawah MPLv2.0[1]BahasaDaftarAfrikaans, Albania, Amhara, Arab, Armenia, Ass...

 

Palais de l'Élysée

Pour les articles homonymes, voir Élysée. Palais de l'ÉlyséeLa façade du palais vue depuis la cour d'honneur.PrésentationType Hôtel particulierDestination initiale Hôtel particulier de Louis-Henri de La Tour d'AuvergneDestination actuelle Bureau et résidence officielle du président de la République françaiseStyle ClassiqueArchitecte Armand Claude MolletConstruction 1718 - 1722Ouverture 1722Commanditaire Louis-Henri de La Tour d'AuvergnePropriétaire État françaisPatrimonialité...

Ludwig Field

Multipurpose athletic facility at the University of Maryland Kehoe Track at Ludwig FieldLudwig FieldThe stadium during a soccer match in 2019Full nameKehoe Track at Ludwig FieldLocationUniversity Boulevard and Stadium Drive University of Maryland College Park, Maryland 20742Coordinates38°59′17.3″N 76°57′02.0″W / 38.988139°N 76.950556°W / 38.988139; -76.950556OwnerUniversity of MarylandOperatorUniversity of MarylandCapacity7,000SurfaceSoccer - Bermuda Grass ...

 

Imad Najah

Moroccan footballer (born 1991) Imad Najah Najah with PSV U23 in 2010Personal informationDate of birth (1991-02-19) 19 February 1991 (age 33)Place of birth Utrecht, NetherlandsPosition(s) Defensive midfielderYouth career USV Elinkwijk2001–2012 PSVSenior career*Years Team Apps (Gls)2012–2016 RKC Waalwijk 33 (1)2017 Jong Vitesse 11 (2)2017–2022 DHSC International career2012 Morocco U23 2 (0) *Club domestic league appearances and goals Imad Najah (born 19 February 1991) is a Moroccan ...

 

Bushwood

This article is about the hamlet in Warwickshire, England. For the community in the United States, see Bushwood, Maryland. For the area in Leytonstone, East London, see Bushwood, Leytonstone. This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bushwood – news · newspapers · books · scholar · JSTOR (February 2018) (Learn how and w...

Alligator Point, Florida

Unincorporated community in Florida, United StatesAlligator PointUnincorporated communityThe Marina at Alligator Point during the 1960sAlligator PointCoordinates: 29°54′18″N 84°25′01″W / 29.905°N 84.417°W / 29.905; -84.417CountryUnited StatesStateFloridaCountyFranklinGovernment • BodyFranklin County, Florida • District 2 CommissionerBert B. Bolt IIPopulation (2012) • Total447 Rough Estimate; Not Conducted by th...

 

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

 

Hans-Jürgen Ripp

German footballer (1946–2021) You can help expand this article with text translated from the corresponding article in German. (June 2022) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated...

Los Marcianos (científicos)

Leo Szilard El planeta Marte Los Marcianos era un término usado para referirse informalmente a un grupo de prominentes científicos húngaros (en su mayoría, aunque no exclusivamente, físicos y matemáticos) que emigraron a los Estados Unidos en la primera mitad del siglo XX.[1]​ Leó Szilárd, quien en broma sugirió que Hungría era un escondite para los extraterrestres de Marte, fue quien dio origen a este término. En respuesta a la pregunta de por qué no hay evidencia de v...

 

سفارة فلسطين في القاهرة

سفارة فلسطين في القاهرة فلسطين مصر البلد مصر  المكان الجيزة العنوان 24 شارع النهضة، الدقي الاختصاص مصر  السَفير دياب اللوح (منذُ 1 نوفمبر 2017) الموقع الالكتروني www.palemb.com تعديل مصدري - تعديل   سَفارة فِلسطين في القاهرة (بالإنجليزية: Embassy of Palestine in Cairo)‏ هي الممثلية الدبلو�...

 

Daming Palace

Archaeological site and history museum in Shaanxi, ChinaDaming Palace National Heritage Park大明宫国家遗址公园The reconstructed Danfeng Gate, housing and conserving the on-site ruins of the original gate of the Daming Palace [1]Established1 October 2010LocationXi'an, Shaanxi, ChinaCoordinates34°17′45″N 108°57′30″E / 34.29583°N 108.95833°E / 34.29583; 108.95833TypeArchaeological site and history museumDaming PalaceSimplified Chinese大明�...

شارع المدينة المنورة (عمان)

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) تقاطع ...

 

Medchal Assembly constituency

Constituency of the Telangana Legislative Assembly, India MedchalConstituency No. 43 for the Telangana Legislative AssemblyConstituency detailsCountryIndiaRegionSouth IndiaStateTelanganaDistrictMedchal–MalkajgiriLS constituencyMalkajgiriEstablished1952Total electors432,202ReservationNoneMember of Legislative Assembly3rd Telangana Legislative AssemblyIncumbent Chamakura Malla Reddy Party  BRSElected year2018 Medchal Assembly constituency is a constituency in Medchal–Malkajgiri di...

 

Paok bakau

Paok bakau Paok bakau di Singapura Status konservasi Punah EXSingkatan dari Extinct (Punah)  EWSingkatan dari Extinct in the Wild (Punah di Alam Liar)Terancam CRSingkatan dari Critical (Kritis) ENSingkatan dari Endangered (Genting) VUSingkatan dari Vulnerable (Rentan)  NTSingkatan dari Not Threatened (Tidak terancam)Aman LCSingkatan dari Least-Concern (Aman) Hampir Terancam  (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passerifo...

1995 New Brunswick general election

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1995 New Brunswick general election – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message) 1995 New Brunswick general election ← 1991 September 11, 1995 1999 → ← outgoing member...

 

Betti number

Roughly, the number of k-dimensional holes on a topological surface In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of n-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicial complexes or CW complexes), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite. The nth Betti numb...