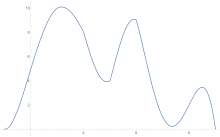
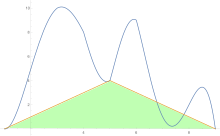
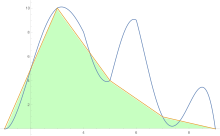
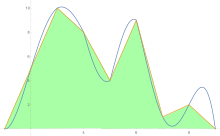
Romberg's method
|
Read other articles:

Ini adalah nama Batak Toba, marganya adalah Manalu. Jimmy Ramoz Manalu Dansatintel Bais TNIPetahanaMulai menjabat 18 Desember 2023 PendahuluBambang HerqutantoPenggantiPetahanaAsintel Kaskogabwilhan IIMasa jabatan27 September 2023 – 18 Desember 2023 PendahuluMuhammad AliPenggantiBambang HerqutantoInspektur Sekolah Staf dan Komando Angkatan DaratMasa jabatan19 April 2022 – 27 September 2023 PendahuluDiding Sutisna SukarmaPenggantiMuhammad AliKomandan Korem 033/Wira Pra...

Katleho Makateng Nazionalità Lesotho Calcio Ruolo Attaccante Squadra Richards Bay Carriera Squadre di club1 2017-2020 Litsilo? (?)2020-2022 LDF? (?)2022- Richards Bay? (?) Nazionale 2022- Lesotho5 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Statistiche aggiornate all'11 maggio 2023 Modifica dati su Wikidata · Manuale Katleho Makateng (Pitseng, 20 settembre 1998) �...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Anies - MuhaiminKampanye untukPemilihan umum Presiden Indonesia 2024KandidatAnies BaswedanGubernur DKI Jakarta (2017–2022)Muhaimin IskandarWakil Ketua DPR RI (2019–sekarang)AfiliasiKoalisi PerubahanStatusDidaftarkan:19 Oktober 2023Diresmikan:13 November 2023Tokoh kunciMuhammad Syaugi (Captain Timnas AMIN) Sudi...

مرسيدس بنز دبليو 116معلومات عامةالنوع طراز سيارة الفئة مرسيدس بنز الفئة إس العلامة التجارية مرسيدس-بنز المصنع مرسيدس بنزالإنتاج 1972التجميع زيندلفينغن المحرك وناقل الحركةالمحرك محرك بنزين الأبعادقاعدة الإطارات 2,865 مـم (112.8 بوصة) , SEL: 2,965 مـم (116.7 بوصة)الطول 4,960 مـ...

British post-hardcore band This article is about the Welsh band. For other bands with similar names, see Blackout (disambiguation). This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Blackout band – news · newspapers · books · scholar · JSTOR (September 2010) (Learn how and when to remove this template message) The BlackoutThe Blackout performing ...

Mughal-e-AzamPoster rilis teatrikalSutradaraK. AsifProduserShapoorji PallonjiDitulis olehAmanKamal AmrohiK. AsifWajahat MirzaEhsan RizviPemeranPrithviraj KapoorDilip KumarMadhubalaDurga KhotePenata musikNaushadSinematograferR. D. MathurPenyuntingDharamvirPerusahaanproduksiSterling Investment CorporationTanggal rilis5 Agustus 1960Durasi197 menitNegaraIndiaBahasaHindiUrduAnggaran₹10.5–15 jutaPendapatankotor₹110 juta[1] Mughal-e-Azam (Indonesia: Kaisar Mughal) adala...

Нескученский лесукр. Нескучненський ліс Расположение 47°48′ с. ш. 36°50′ в. д.HGЯO Страна Украина ОбластьДонецкая область РайонВолновахский район Нескученский лес Нескученский лес Медиафайлы на Викискладе Нескученский лес — ландшафтный заказник мест...

French singer (born 1946) Géraldine Gogly[1][2](born 18 April 1946 in Paris[3]) is a French singer. Biography She started her career in 1966 with the label Polydor, releasing a 45' EP La rivière me disait (The river has said to me). Guy Lux then invited her to perform in his show Le Palmarès des chansons. She has performed in the debut of Enrico Macias at L'Olympia. She represented Switzerland in the Eurovision Song Contest 1967 in Vienna with the song Quel cœur va...

1990 live album by Max Roach and Dizzy GillespieMax + Dizzy: Paris 1989Live album by Max Roach and Dizzy GillespieReleased1990RecordedMarch 23, 1989VenueMaison de la Culture de la Seine-Saint-Denis, Bobigny, FranceGenreJazzLength125:52LabelA&M CD 6404ProducerJohn SnyderDizzy Gillespie chronology Live at the Royal Festival Hall(1989) Max + Dizzy: Paris 1989(1990) The Paris All Stars Homage to Charlie Parker(1989) Max Roach chronology Bright Moments(1986) Max + Dizzy: Paris 1989(198...

British TV comedy series (1990–1998) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Harry Enfield & Chums – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this message) Harry Enfield & ChumsAlso known asHarry Enfield's Television ProgrammeHarry Enfield Pres...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

Russian actor and comedian In this name that follows Eastern Slavic naming customs, the patronymic is Viktorovich and the family name is Khazanov. Gennady KhazanovГеннадий ХазановBornGennady Viktorovich Khazanov (1945-12-01) 1 December 1945 (age 78)Moscow, Russian SFSR, Soviet UnionOccupation(s)Actor, humorist, parodistYears active1967–presentTitlePeople’s Artist of the RSFSR (1991)Awards Full cavalier of the Order For Merit to the Fatherland Order of Friendsh...

British politician (born 1982) Will QuinceOfficial portrait, 2023Minister of State for Health and Secondary Care[a]In office8 September 2022 – 13 November 2023Prime MinisterLiz TrussRishi SunakPreceded byMaria CaulfieldSucceeded byAndrew StephensonMinister of State for School StandardsIn office7 July 2022 – 7 September 2022Prime MinisterBoris JohnsonPreceded byRobin WalkerSucceeded byJonathan GullisParliamentary Under-Secretary of State for Children and FamiliesI...

The Weightlifting events at the 2010 Commonwealth Games were held at the Jawaharlal Nehru Stadium, Delhi from 4 to 12 October 2010. Weightlifting medal count * Host nation (India)RankNationGoldSilverBronzeTotal1 Nigeria (NGR)545142 Samoa (SAM)30033 India (IND)*22484 Australia (AUS)22155 Canada (CAN)2125 Malaysia (MAS)21257 Nauru (NRU)11028 New Zealand (NZL)02029 Sri Lanka (S...

Kota Pagar Alam PagaralamKotaKota Pagar AlamTranskripsi bahasa daerah • Abjad Jawiڤاڬر عالم • Surat Uluꤶꤱꥑꥆꤾꤸ꥓Dari Atas, Kiri ke kanan: Gunung Dempo, Tari Kebagh Khas Pagar Alam, Kawasan Taman Kota, Perkebunan Teh di kawasan Gunung Dempo LambangMotto: Besemah Kota Perjuangan[a]Letak kota Pagar Alam di Sumatera SelatanKota Pagar AlamLetak kota Pagar Alam di Sumatera SelatanTampilkan peta SumatraKota Pagar AlamKota Pagar Alam (Indo...

Sports arena in Peristeri, west Athens, Greece Peristeri Olympic Boxing HallFull namePeristeri Olympic Boxing HallLocationPeristeri, Athens, GreeceCapacityIndoor Arena:8,400 (original capacity)2,305 (current capacity)Football Pitch: 3,000ConstructionOpened2004Construction cost€14.7 million euros (2004 money) 38°00′47″N 23°42′59″E / 38.01306°N 23.71639°E / 38.01306; 23.71639 The Peristeri Olympic Boxing Hall is an indoor arena that is located in Peristeri,...

Soviet chess grandmaster (1911–1995) In this name that follows Eastern Slavic naming customs, the patronymic is Moiseyevich and the family name is Botvinnik. Mikhail BotvinnikBotvinnik in 1962Full nameMikhail Moiseyevich BotvinnikCountrySoviet UnionBorn(1911-08-17)August 17, 1911Kuokkala, Grand Duchy of Finland, Russian EmpireDiedMay 5, 1995(1995-05-05) (aged 83)Moscow, RussiaTitleGrandmaster (1950)World Champion1948–19571958–19601961–1963Peak rating2630 (July 1971)...

У этого термина существуют и другие значения, см. Солсбери (значения). ГородСолсбериSalisbury Солсберийский собор 51°04′26″ с. ш. 1°47′36″ з. д.HGЯO Страна Великобритания Регион Юго-Западная Англия Церемониальное графство Уилтшир История и география Площадь 11,3 км�...

For other uses, see Xinzhou (disambiguation). Not to be confused with Qinzhou. Prefecture-level city in Shanxi, People's Republic of ChinaXinzhou 忻州市Prefecture-level cityFoguang Temple in Wutai CountyLocation of Xinzhou City jurisdiction in ShanxiXinzhouLocation of the city centre in ShanxiCoordinates (Xinzhou Municipal Government): 38°24′58″N 112°44′02″E / 38.416°N 112.734°E / 38.416; 112.734CountryPeople's Republic of ChinaProvinceShanxiCounty-l...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. اضطهاد اليهود اضطهاد اليهود جزء رئيسي من التاريخ اليهودي، وهو ما أدى إلى موجات متنقلة من اللاجئين في مختلف أنحاء مجتمعات الشتات. السلوقيون عندما وقعت منطقة يهودا تحت سلطة ال�...