Polish space
|
Read other articles:

Wilayah Hulu Sungai warna biru tua yang sekarang terdiri dari enam kabupaten yang disebut Banua Enam. Afdeeling Hoeloe Soengai (1930)[1] /Hoeloe Soengei Ken Riken (1942)[2]/Kabupaten Hulu Sungai (1950) adalah bekas afdeling pada masa pemerintahan Hindia Belanda/Jepang dengan wilayah di sepanjang daerah aliran sungai (DAS) Negara (sungai Bahan) di provinsi Kalimantan Selatan.[3][4] Pada Bulan April 1950 DR Murdjani diangkat sebagai Gubernur Kalimantan. Kemuadian...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Hungry Ghosts: Mao's Secret Famine PengarangJasper BeckerNegaraBritania RayaBahasaInggrisGenreSejarahPenerbitHolt Paperbacks pada 15 April 1998Tanggal terbit15 April 1998Jenis mediaCetak (Sampul keras)ISBNISBN 0805056688 Hungry Ghosts: Mao's ...

Artikel ini memberikan informasi dasar tentang topik kesehatan. Informasi dalam artikel ini hanya boleh digunakan untuk penjelasan ilmiah; bukan untuk diagnosis diri dan tidak dapat menggantikan diagnosis medis. Wikipedia tidak memberikan konsultasi medis. Jika Anda perlu bantuan atau hendak berobat, berkonsultasilah dengan tenaga kesehatan profesional. Distemper anjingInformasi umumNama lainHard pad disease, food pad diseaseSpesialisasiKedokteran hewanPenyebabCanine morbillivirus (dulu diseb...

TV station in Houston For the station on channel 10 with a similar call sign, see KUVM-LD. KUVM-CDHouston, TexasUnited StatesChannelsDigital: 20 (UHF)Virtual: 34BrandingKUVM-CD 34 Missouri City, TXProgrammingSubchannels(see below)Affiliations(see below)OwnershipOwnerHC2 Holdings(HC2 LPTV Holdings, Inc.)Sister stationsKEHO-LD, KUGB-CD, KUVM-LD, KBMN-LDHistoryFoundedAugust 6, 1980First air dateNovember 30, 1981; 42 years ago (1981-11-30)Former call signsK55CP (1981–1989)K53C...

Italian footballer and manager Lido Vieri Vieri c. 1970Personal informationFull name Lido VieriDate of birth (1939-07-16) 16 July 1939 (age 84)Place of birth Piombino, ItalyHeight 1.83 m (6 ft 0 in)Position(s) GoalkeeperYouth career1954–1957 TorinoSenior career*Years Team Apps (Gls)1957–1969 Torino 275 (0)1957–1958 → Vigevano (loan) 31 (0)1969–1976 Inter Milan 140 (0)1976–1980 Pistoiese 63 (0)Total 499 (0)International career1963–1968 Italy 4 (0)Managerial ca...

Defensive strategy in basketball Basketball playbook2–3 zone initial alignment2–3 zone DefenseType:Half court zone defenseName UsageTechnical name:2–3 zone DefenseCommon name:2–3 zoneOther common names:2–1–2 zonePlay Development CreditDesigned 1st by:Coach Cam HendersonYear play 1st used:1914Play 1st used by:Bristol high schoolCountry:United States The 2–3 zone defense is a defensive strategy used in basketball as an alternative to man-to-man defense. It is referred to as the 2�...
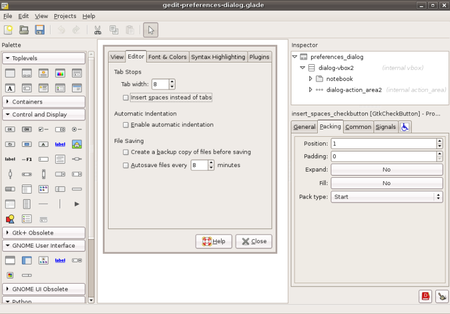
Glade Designing a preferences dialog in GladeTipealat pemrograman Versi pertamaApril 18, 1998Versi stabil 3.40.0 (10 Agustus 2022) GenreGUI designerLisensiGNU General Public LicenseBagian dariThe GNOME Project (en) Karakteristik teknisSistem operasiCross-platformBahasa pemrogramanC Antarmuka BibliotecaGTK Sumber kode Kode sumberPranala Debianglade Arch Linuxglade Ubuntuglade Gentoodev-util/glade Fedoraglade Informasi tambahanSitus webhttp://glade.gnome.orgPelacakan kesalahanLaman pelacakan Fr...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Benetton GroupJenisSocietà a responsabilità limitataIndustriBusanaDidirikan1965; 59 tahun lalu (1965) di Ponzano Veneto, ItaliaPendiriLuciano Benetton Carlo Benetton Giuliana BenettonKantorpusatPonzano Veneto, ItaliaWilayah operasiDuniaTokohkunciLuciano Benetton (CEO)Tommaso Brusò (Chief Operating Officer)ProdukPakaianSepatuTasAksesoris busanaKaryawan7,714 (2015)Situs webwww.benettongroup.com United Colors of Benetton di Parma, Italia. United Colors of Benetton di Prague, Republik Cek...

Stasiun Cibitung C24 Stasiun Cibitung arah Timur, 2019LokasiJalan Bosih RayaWanasari, Cibitung, Bekasi, Jawa Barat 17521IndonesiaKoordinat6°15′46″S 107°4′49″E / 6.26278°S 107.08028°E / -6.26278; 107.08028Koordinat: 6°15′46″S 107°4′49″E / 6.26278°S 107.08028°E / -6.26278; 107.08028Ketinggian+19 mOperator KAI Commuter Letakkm 36+779 lintas Jakarta–Jatinegara–Cikampek[1] Jumlah peron1 peron pulauJumlah jalur2: ja...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

etiquette You asked where it says not to change portions of articles under RFC review during an active RFC... I don't have time to dig around WP:RFC, however it's just kinda common sense. If an editor responds to the RFC, and makes comments on version X, and there have been 4 changes since version X, the next editor to respond isn't going to understand other editors' comments and the development of consensus is severely hindered. Beyond that, it's just general wiki etiquette. Not everything ...

County in Heilongjiang, People's Republic of ChinaBaiquan County 拜泉县CountyBaiquanLocation in HeilongjiangCoordinates: 47°35′N 126°01′E / 47.583°N 126.017°E / 47.583; 126.017CountryPeople's Republic of ChinaProvinceHeilongjiangPrefecture-level cityQiqiharTownship-level divisions7 towns9 townshipsCounty seatBaiquan Town (拜泉镇)Area • Total3,569 km2 (1,378 sq mi)Elevation233 m (764 ft)Population • Total570...

Election of Pope Innocent II Papal election 1130Dates and location14 February 1130monastery of S. Gregorio, RomeKey officialsDeanPietro SenexElected popeGregorio PapareschiName taken: Innocent II← 11241143 → The 1130 papal election (held February 14) was convoked after the death of Pope Honorius II and resulted in a double election. Part of the cardinals, led by Cardinal-Chancellor Aymeric de la Chatre, elected Gregorio Papareschi as Pope Innocent II, but the rest of them refuse...

Sporting event delegationPuerto Rico at the1948 Summer OlympicsIOC codePURNOCPuerto Rico Olympic CommitteeWebsitewww.copur.pr (in Spanish)in LondonCompetitors9 (9 men, 0 women) in 3 sportsFlag bearerJosé ‘Fofó’ Vicente[1]MedalsRanked 34th Gold 0 Silver 0 Bronze 1 Total 1 Summer Olympics appearances (overview)19481952195619601964196819721976198019841988199219962000200420082012201620202024 Puerto Rico competed in the Summer Olympic Games for the first time at the 1948 S...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Deutz AG – berita · surat kabar · buku · cendekiawan · JSTOR (April 2008) Deutz AGJenisAktiengesellschaftKode emitenFWB: DEZIndustriTeknik mesinDidirikan31 Maret 1864; 160 tahun lalu (1864-03-31)PendiriN...

4 Heures de Spa 2017 4 Heures de Spa 2017Généralités Sport Endurance Organisateur(s) Automobile Club de l'Ouest Lieu(x) Francorchamps Wallonie Belgique Date Le 24 septembre 2017 Participants 35 Site(s) Circuit de Spa-Francorchamps Palmarès Tenant du titre DragonSpeed Vainqueur Graff Navigation Édition précédente Édition suivante modifier Les 4 Heures de Spa-Francorchamps 2017, disputées le 24 septembre 2017 sur le Circuit de Spa-Francorchamps sont la cinquième manche de l'Euro...

In matematica, in particolare in analisi complessa, si definisce funzione meromorfa su un sottoinsieme aperto D {\displaystyle {\mathcal {D}}} del piano complesso una funzione che è olomorfa su tutto D {\displaystyle {\mathcal {D}}} ad esclusione di un insieme di punti isolati che sono poli della funzione stessa. Ogni funzione meromorfa su D {\displaystyle {\mathcal {D}}} può essere espressa come rapporto di due funzioni olomorfe (con la funzione denominatore diversa dalla costante 0) defin...

Liste des sportifs kényans (par sport et par chronologie) médaillés d'or lors des Jeux olympiques d'été et d'hiver, à titre individuel ou par équipe, de 1956 à 2008. Jeux olympiques d'été Athlétisme Nom Discipline(s) Année(s) Kipchoge Keino 1 500 m (H) 1968 Naftali Temu 10 000 m (H) 1968 Amos Biwott 3 000 m steeple (H) 1968 Kipchoge Keino 3 000 m steeple (H) 1972 Charles AsatiHezahiah NyamauRobert OukoJulius Sang Relais 4 × 400 m (H) 1972 Julius Korir 3&#...

School or college, often providing an Islamic education Not to be confused with Madras, Madrasi, or Madrasta. Madraseh, Medrese, and Madraza redirect here. For other uses, see Madrasa (disambiguation). The three madrasas at the Registan of Samarkand, built during the Timurid Renaissance Part of a series onIslam Beliefs Oneness of God Angels Revealed Books Prophets Day of Resurrection Predestination Practices Profession of Faith Prayer Almsgiving Fasting Pilgrimage TextsFoundations Quran Sunna...
