Odds algorithm
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Paul HüttelLahir13 Juli 1935 (umur 88)Hedensted, DenmarkPekerjaanPemeranTahun aktif1960-kini Paul Hüttel (lahir 13 Juli 1935) adalah seorang pemeran asal Denmark. Ia tampil dalam lebih dari 50 film dan acara televisi sejak 1960. Ia membinta...

Yearly conference held for climate change treaty negotiations 2023 United Nations Climate Change ConferenceLogoA group photo of national leaders and other dignitaries at the 2023 United Nations Climate Change ConferenceNative name مؤتمر الأمم المتحدة للتغير المناخي 2023Date30 November – 13 December 2023 (2023-11-30 – 2023-12-13)LocationExpo City, Dubai, United Arab EmiratesOrganised byUnited Arab EmiratesParticipantsUNFCCC m...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الخبر الأسبوعيمعلومات عامةالنوع أسبوعيةبلد المنشأ الجزائر الثمن 10 دجشخصيات هامةرئيس التحرير كمال ز�...

Sukhoi Su-24Su-24 Soviet dengan roda diturunkan.TipePesawat serang daratProdusenSukhoiTerbang perdanaDesember 1971Diperkenalkan1974StatusAktifPengguna utamaRusiaPengguna lainIranSiriaJumlah produksi1200+ Sukhoi Su-24 pada MAKS Airshow 2005. Sukhoi Su-24 (kode NATO: 'Fencer') adalah sebuah pesawat penyerang segala cuaca supersonik Uni Soviet yang paling maju pada tahun 1970-1980an. Pesawat ini diawaki dua orang, mempunyai dua mesin dan merupakan pesawat Soviet pertama yang memiliki perangkat n...

Maip Periode Kapur Akhir, Maastrichtian PreЄ Є O S D C P T J K Pg N Material yang diketahui: (A), rekonstruksi rongga torakik pada tingkat keenam vertebra torakik (B), dan penggambaran interpretatif dari wilayah penggalian (C)TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSaurischiaFamiliMegaraptoridaeGenusMaip Tata namaDinamakan berdasarkanMaip (en) lbs Maip adalah sebuah genus dinosaurus theropoda megaraptoridae yang berasal dari lapisan batuan Periode Kapur Akhir (Maastrichtium)...

علي موسوي معلومات شخصية الاسم الكامل سيد علي موسوي الميلاد 22 أبريل 1976 (العمر 47 سنة)[1]المحمرة، إيران الطول 1.86 م (6 قدم 1 بوصة) مركز اللعب مهاجم الجنسية إيران مسيرة الشباب سنوات فريق هما 0000–1996 باس طهران المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1996–1998 باس طهران 19...

The building designed by Sam Scorer at Markham Moor services (sometimes known as the Markham Moor Petrol Station, Markham Moor Hypar or Markham Moor Papilo) is a Grade II listed building originally designed as a petrol station. It is located on the A1 south-bound at the Markham Moor junction services and was built between 1959 and 1960 with the aid of engineer Dr Kalman Hajnal-Kónyi. It is currently a Starbucks.[1] Building in Markham Moor junction servicesMarkham Moor Scorer Buildin...

Mother of Adolf Hitler (1860–1907) Klara HitlerKlara Pölzl in the 1870sBornKlara Pölzl(1860-08-12)12 August 1860Spital, Weitra, Austrian EmpireDied21 December 1907(1907-12-21) (aged 47)Linz, Austria-HungaryResting placeTown Cemetery, LeondingNationalityAustro-HungarianKnown forMother of Adolf HitlerSpouse Alois Hitler (m. 1885; died 1903)ChildrenGustavIdaOttoAdolfEdmundPaulaParentsJohann Baptist PölzlJohanna HiedlerRelativesJ...

Complex enzyme found in bacteria, archaea, and mitochondria of eukaryotes Cytochrome c oxidaseThe crystal structure of bovine cytochrome c oxidase in a phospholipid bilayer. The intermembrane space lies to top of the image. Adapted from PDB: 1OCC (It is a homodimer in this structure)IdentifiersEC no.1.9.3.1CAS no.9001-16-5 DatabasesIntEnzIntEnz viewBRENDABRENDA entryExPASyNiceZyme viewKEGGKEGG entryMetaCycmetabolic pathwayPRIAMprofilePDB structuresRCSB PDB PDBe PDBsumGene OntologyAmiGO...

Town of Mexico This article may be a rough translation from Spanish. It may have been generated, in whole or in part, by a computer or by a translator without dual proficiency. Please help to enhance the translation. The original article is under español in the languages list. See this article's entry on Pages needing translation into English for discussion. (January 2020) Town in MexicoVilla Insurgentes El CalabazalTownVilla InsurgentesVilla InsurgentesShow map of ZacatecasVilla Insurgente...

Saint Georgije BogićHoly hieromartyrBorn(1911-02-06)6 February 1911Pakrac, Kingdom of Croatia-Slavonia, Austria-HungaryDied17 June 1941(1941-06-17) (aged 30)Našice, Independent State of CroatiaVenerated inEastern Orthodox ChurchCanonized1998, Belgrade by Serbian Orthodox ChurchFeast17 June (O.S. 4 June)AttributesVested as a protopresbyter Đorđe Bogić (Serbian Cyrillic: Ђорђе Богић; 6 February 1911 – 17 June 1941) was a protopresbyter in the Serbian Orthodox Church a...

Folignocomune (dettagli) Foligno – VedutaPanorama LocalizzazioneStato Italia Regione Umbria Provincia Perugia AmministrazioneSindacoStefano Zuccarini (LSP) dal 9-6-2019 TerritorioCoordinate42°57′22″N 12°42′12″E / 42.956111°N 12.703333°E42.956111; 12.703333 (Foligno)Coordinate: 42°57′22″N 12°42′12″E / 42.956111°N 12.703333°E42.956111; 12.703333 (Foligno) Altitudine234 m s.l.m. Superficie264,67 km...

Williams nel 2017 Mark Williams (Bromsgrove, 22 agosto 1959) è un attore, comico e sceneggiatore britannico. È noto principalmente per aver interpretato Arthur Weasley nei film tratti dalla saga di Harry Potter e l'omonimo protagonista nella serie TV della BBC Padre Brown. Indice 1 Biografia 2 Filmografia parziale 2.1 Cinema 2.2 Televisione 3 Doppiatore 4 Doppiatori italiani 5 Altri progetti 6 Collegamenti esterni Biografia Dal pubblico britannico è conosciuto principalmente come uno dei p...
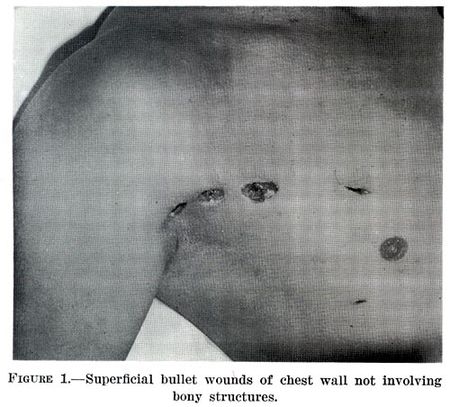
LukaLuka pada badan seorang priaInformasi umumSpesialisasiKedokteran gawat darurat Luka (bahasa Inggris: wound) adalah cedera yang muncul dengan cepat dan melibatkan kerusakan kulit (luka terbuka) atau memar (luka tertutup) akibat trauma fisik. Dalam patologi, luka adalah cedera akut yang merusak epidermis kulit. Berdasarkan Bahasa Indonesia, luka memiliki beberapa penyebutan sesuai letak luka itu berada. Contohnya luka yang terletak pada kepala di sekitar tumbuhnya rambut disebut 'pitak'. Se...

American politician Chester A. Dolan Jr.Chester A. Dolan Jr.President of the Massachusetts SenateIn office1949–1950Preceded byHarris S. RichardsonSucceeded byHarris S. RichardsonMember of the Massachusetts Senate from the 5th Suffolk DistrictIn office1939–1950Preceded byJames W. Hennigan Sr.Succeeded byJohn F. CollinsMember of theMassachusetts House of Representativesfrom the 10th Suffolk DistrictIn office1937–1939 Personal detailsBorn(1907-09-20)September 20, 1907Boston, MassachusettsD...
Al-Suqaylabiyya (ar) السقيلبيه Administration Pays Syrie Muhafazah (محافظة) Gouvernorat de Hama Démographie Population 17 313 hab. (2004) Géographie Coordonnées 35° 13′ nord, 36° 13′ est Altitude 220 m Localisation Géolocalisation sur la carte : Syrie Al-Suqaylabiyya modifier Al-Suqaylabiyya (arabe : السقيلبيه, prononcée as-Suqailabiyya) est une ville de Syrie dont la population est constituée en majo...

將軍巴育·占奥差ประยุทธ์ จันทร์โอชา上將 MPCh MWM TChW 泰國樞密院議員现任就任日期2023年11月29日君主拉瑪十世議長素拉育·朱拉暖 泰國第29任總理任期2022年9月30日復職—2023年8月22日君主拉瑪十世副總理(英语:Deputy Minister of Thailand) 列表 巴威·翁素万塔那塞·巴滴玛巴功(英语:Thanasak Patimaprakorn) 威沙努·革岸(英语:Wissanu Krea-ngam) 比蒂耶�...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

Cet article est une ébauche concernant l’art et une chronologie ou une date. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Données clés 1745 1746 1747 1748 1749 1750 1751Décennies :1710 1720 1730 1740 1750 1760 1770Siècles :XVIe XVIIe XVIIIe XIXe XXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الحبيب التوهامي وزير الصحة العمومية التونسي في المنصب14 أكتوبر 1983 – 20 يناير 1984 (3 أشهرٍ و6 أيامٍ) الرئيس ال�...



































