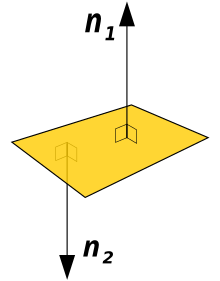
Normal (geometry)
|
Read other articles:

Untuk kegunaan lain, lihat La Toya (disambiguasi). La Toya JacksonJackson pada tahun 2011LahirLa Toya Yvonne Jackson15 Januari 1956 (umur 68)Gary, Indiana, Amerika SerikatNama lainToyToyaPekerjaanPenyanyi–penulis laguaktrisaktivisfilantropismodelpenulispebisnisselebriti [1]Tahun aktif1972–sekarangSuami/istriJack Gordon (m. 1989; c. 1997)[2][3]PasanganBobby DeBarge(1977–1982)[4]Karier musik...

Italian football manager (born 1977) Fabio Grosso Grosso with Frosinone in 2022Personal informationFull name Fabio Grosso[1]Date of birth (1977-11-28) 28 November 1977 (age 46)Place of birth Rome, ItalyHeight 1.90 m (6 ft 3 in)Position(s) Left-backYouth career1994–1995 Renato CuriSenior career*Years Team Apps (Gls)1995–1999 Renato Curi 125 (55)1999–2001 Chieti 68 (17)2001–2004 Perugia 67 (7)2004–2006 Palermo 90 (2)2006–2007 Inter Milan 23 (2)2007–2009...

Chengdu ShuangliuInternational Airport成都双流国际机场Chéngdū Shuāngliú Guójì JīchǎngIATA: CTUICAO: ZUUUInformasiJenisPublicPengelolaSichuan Province Airport Group Co.,LtdMelayaniChengduLokasiShuangliu CountyMaskapai penghubungAir ChinaChengdu AirlinesSichuan AirlinesKetinggian dpl495 mdplSitus webwww.cdairport.comPetaCTULocation in SichuanLandasan pacu Arah Panjang Permukaan m kaki 02L/20R 3,600×45 11,181 Aspal/Beton 02R/20L 3,600×60 11,181 Beton Statistik (2011)P...

German art historian and museum director (1844–1933) Karl Woermann (4 July 1844 – 4 February 1933) was a German art historian and museum director. Biography He was born in Hamburg, studied at various universities (art history at Heidelberg and Munich), and traveled widely. In 1871 Woermann participated in the so-called Holbein convention in Dresden, at which a number of prominent art historians convened to determine which of two versions of Hans Holbein the Younger's Meyer Madonna was the...

Band of indigenous people in Canada Alderville First Nation Band Office Alderville First Nation is a band of Mississaugas, a sub-nation of the Ojibways. The Alderville and Sugar Island 37A reserves belong to that First Nation band government. First Nation The Alderville First Nation is an Anishinaabe First Nation located in southern Ontario, Canada. As of December 2017, Alderville First Nation had 1,162 registered band members, of which their on-Reserve population was only 323 people, meaning...

For other uses, see Slatina (disambiguation). RiverSlatinaThe Slatina in ZvolenPhysical characteristicsMouth • locationHron • coordinates48°33′41″N 19°06′22″E / 48.5614°N 19.1061°E / 48.5614; 19.1061Length53 km (33 mi)Basin size793 km2 (306 sq mi)Basin featuresProgressionHron→ Danube→ Black Sea The Slatina is a river in Slovakia. Its source is located in the mountain range Poľana,...

English Professor of Hebrew and Divinity For the New Zealand rugby union player, see Alexander Kirkpatrick (rugby union). Memorial to Alexander Francis Kirkpatrick in Ely Cathedral Alexander Francis Kirkpatrick (25 June 1849 – 22 January 1940) was Regius Professor of Hebrew at Cambridge University (1882–1903) and the third Master of Selwyn College, Cambridge (1898–1907). Life Kirkpatrick was born at Lewes, East Sussex, only son (with three daughters) of Rev. Francis Kirkpatrick, and was...

2014 single by Alicia KeysWe Are HereSingle by Alicia KeysReleasedSeptember 15, 2014 (2014-09-15)GenreR&BLength4:44LabelRCASongwriter(s) Alicia Keys Swizz Beatz Mark Batson Harold Lilly Producer(s) Alicia Keys Swizz Beatz Mark Batson Harold Lilly Alicia Keys singles chronology It's On Again (2014) We Are Here (2014) 28 Thousand Days (2015) Music videoWe Are Here on YouTube We Are Here is a song by American recording artist Alicia Keys. It was written and produced by Keys, S...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Serie C2 1990-1991 Competizione Serie C2 Sport Calcio Edizione 13ª Organizzatore Lega Professionisti Serie C Date dal 16 settembre 1990al 30 giugno 1991 Luogo Italia Partecipa...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Nowhere ManAlbum mini karya The BeatlesDirilis8 Juli 1966 (1966-07-08)Direkam1965, EMI Studios, LondonGenreRockDurasi11:11LabelParlophoneProduserGeorge MartinKronologi The Beatles Yesterday(1966)Yesterday1966 Nowhere Man (1966) Magical Myste...

French journalist, politician, and French Resistance leader Georges MandelGeorges Mandel (5 June 1885 – 7 July 1944) was a French Jewish journalist, and politician. Early life Born Louis George Rothschild in Chatou, Yvelines, he was the son of a tailor and his wife. His family was Jewish, originally from Alsace.[1] They moved into France in 1871 to preserve their French citizenship when Alsace-Lorraine was annexed by the German Empire at the end of the Franco-Prussian War. Early car...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: George Smoot – berita · surat kabar · buku · cendekiawan · JSTOR George Smoot George Fitzgerald Smoot III (lahir 20 Februari 1945) adalah fisikawan astrofisik (ahli astrofisika) dari Amerika Serikat dan ...

Voce principale: Coppa Intercontinentale. Coppa Intercontinentale 2016 Competizione Coppa Intercontinentale Sport hockey su pista Edizione 16ª Luogo Spagna Partecipanti 2 Sede finale Vic Risultati Vincitore Vic Finalista Huracán Statistiche Incontri disputati 1 Gol segnati 6 (6 per incontro) Cronologia della competizione 2014 2017 Manuale La Coppa Intercontinentale 2016 è stata la 16ª edizione dell'omonima competizione di hockey su pista riservata alle squadre di c...

Liceo classico statale Cesare Beccaria UbicazioneStato Italia CittàMilano IndirizzoVia Carlo Linneo, 5 OrganizzazioneTipoLiceo classico Ordinamentopubblico Fondazione1603 PresideLaura Gamba Mappa di localizzazione Sito web Modifica dati su Wikidata · Manuale Il liceo classico statale Cesare Beccaria di Milano è uno dei più antichi istituti scolastici presenti e attivi in Italia. Indice 1 Le scuole arcimbolde 2 Il collegio di Sant'Alessandro 3 Il Beccaria 4 Altri progetti 5 Colle...

American television film Not to be confused with Saving Lincoln. Killing LincolnFilm posterGenreDocudramaBiographyBased onKilling Lincolnby Bill O'ReillyDeveloped byTony ScottWritten byErik JendresenDirected byAdrian MoatPresented byTom HanksStarringBilly CampbellJesse JohnsonComposerDavid BuckleyCountry of originUnited StatesOriginal languageEnglishProductionExecutive producersMark HerzogErik JendresenBill O'ReillyMary LisioTeri WeinbergDavid W. ZuckerProducersRidley ScottTony ScottChristoph...

American Arctic explorer Ross Gilmore MarvinMarvin in Arctic outerwareBorn(1880-01-28)January 28, 1880Elmira, New York, U.S.Disappearedafter December 8, 1908 (1908-12-08)DiedApril 10, 1909(1909-04-10) (aged 29)near Cape Columbia, CanadaAlma materCornell University, New York Nautical SchoolOccupationCollege instructorKnown forArctic exploration with Robert PearyAwardsPeary Polar Expedition Medal Ross Gilmore Marvin (January 28, 1880 – after December 8, 1908; rep...

Para otros usos de este término, véase Juana II de Nápoles. Juana I de Nápoles Miniatura de una ed. del s. XV o XVI de la obra de Boccaccio De mulieribus claris: la reina Juana. BnF. Reina de Nápoles 20 de enero de 1343-22 de mayo de 1382Predecesor Roberto ISucesor Carlos III Condesa de Provenza y Forcalquier 20 de enero de 1343-22 de mayo de 1382Predecesor Roberto ISucesor Luis I Princesa de Acaya 1373-1381Predecesor Felipe II de TarentoSucesor Jaime de Baux Información personalNombre...

ウジェーヌ・ドラクロワ『民衆を導く自由の女神』(1830年)ルーヴル美術館所蔵。自然法論とは、法的理念による現実の基礎付けあるいは現実との闘争である。 自然法論(しぜんほうろん、英: natural law theory、独: Naturrechtslehre)は、広義においては、自然法に関する法学、政治学ないし倫理学上の諸学説の総称である。 定義 自然法論とは、最広義においては、ギ...

Porträt von France Prešeren (vor 1849) France Prešeren (Francè Prešẹ́ren [franˈt͡sɛ prɛˈʃeːrɛn]; eingedeutscht früher oft Franz Preschern;[1] * 3. Dezember 1800 in Vrba im damaligen Herzogtum Krain; † 8. Februar 1849 in Kranj, damals Krainburg) gilt als größter slowenischer Dichter. Inhaltsverzeichnis 1 Leben 2 Werke 3 Ehrungen 4 Schriften in deutscher Sprache 5 Literatur 6 Weblinks 7 Siehe auch 8 Einzelnachweise Leben Prešerens Geburtshaus in Vrba Gedenktafel in...

Questa voce sull'argomento politici polacchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Adam Struzik Maresciallo del Senato della PoloniaDurata mandato26 ottobre 1993 –19 ottobre 1997 PredecessoreAugust Chełkowski SuccessoreAlicja Grześkowiak Maresciallo del Voivodato della MasoviaIn caricaInizio mandato1º dicembre 2001 PredecessoreZbigniew Kuźmiuk Dati generaliPartito politicoPartito Popolare Unito (1984-1989) Parti...