Necklace splitting problem
|
Read other articles:

Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Bali PostPengemban Pengamal PancasilaTipeHarianFormatHarian koran pagiPemilikKelompok Media Bali PostPenerbitPT Bali PostDidirikan16 Agustus 1948 (umur 75)BahasaBahasa Ind...

Untuk kompetisi tahun ini, lihat L-Men of The Year 2023. The New L-Men of The YearThe New L-Men of The YearTanggal pendirian2004; 20 tahun lalu (2004)TipeKontes priaKantor pusatJakarta, IndonesiaJumlah anggota Mister WorldMister SupranationalMister InternationalBahasa resmi Bahasa IndonesiaOrganisasi indukNutrifood IndonesiaSitus webhttp://www.l-men.com The New L-Men of The Year (atau lebih dulu dikenal sebagai L-Men of The Year, disingkat LoTY) adalah kontes pria yang diadakan oleh Nutr...

Civilian honor awarded by the Soviet Union AwardOrder of LeninOrder of Lenin, Type 4 awarded from 1943 to 1991TypeSingle-grade orderAwarded for outstanding services rendered to the State, exemplary service in the armed forces, promoting friendship and cooperation between people and in strengthening peace, and meritorious services to the Soviet state and society CountrySoviet Union Presented by Soviet UnionEligibilityCitizens of the Soviet Union; foreigners; institutions, enterprise...

City in Donetsk Oblast, Ukraine For other uses, see Kramatorsk (disambiguation). City in UkraineKramatorsk КраматорськCity FlagCoat of armsKramatorskKramatorsk on the map of Donetsk OblastShow map of Donetsk OblastKramatorskKramatorsk (Ukraine)Show map of UkraineCoordinates: 48°44′21″N 37°35′02″E / 48.73917°N 37.58389°E / 48.73917; 37.58389Country UkraineOblast DonetskRaion KramatorskHromadaKramatorsk urbanFounded1868City status since19...

Greek politician and general (died 1868) This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gennaios Kolokotronis – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this template message) Ioannis KolokotronisΙωάννης ΚολοκοτρώνηςA portrait of Ioannis Kolokotronis c. 1860Pr...

Peta menunjukan lokasi Roxas City Roxas City adalah kota yang terletak di provinsi Capiz, Filipina. Pada tahun 2007, kota ini memiliki populasi sebesar 147.738 jiwa. Pembagian wilayah Secara politis Roxas City terbagi menjadi 47 barangay, yaitu: Tiza Bago Balijuagan Banica Barra Bato Baybay Adlawan Cabugao Cagay Cogon Culajao Culasi Dumolog Dayao Dinginan Gabu-an Inzo Arnaldo Village (Cadimahan) Jumaguicjic Lanot Lawa-an Li-ong Libas Loctugan Lonoy Milibili Mongpong Olotayan Punta Cogon Punta...
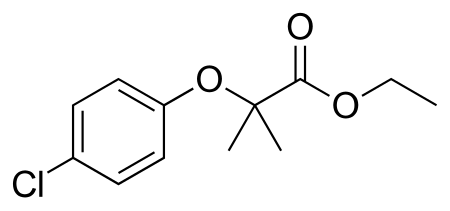
Chemical compound ClofibrateClinical dataAHFS/Drugs.comMicromedex Detailed Consumer InformationPregnancycategory AU: B1 Routes ofadministrationBy mouthATC codeC10AB01 (WHO) Legal statusLegal status US: Discontinued Pharmacokinetic dataProtein bindingVariable, 92–97% at therapeutic concentrationsMetabolismHydrolyzed to clofibric acid; hepatic glucuronidationElimination half-lifeHighly variable; average 18–22 hours. Prolonged in renal failureExcretionRenal, 95 to 9...

Public community college in Virginia, U.S. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Virginia Peninsula Community College – news · newspapers · books · scholar · JSTOR (August 2010) (Learn how and when to remove this message) Virginia Peninsula Community CollegeTypePublic community collegeEstablished19...

Constituency of the Maharashtra legislative assembly in India ShirolConstituency No. 280 for the Maharashtra Legislative AssemblyConstituency detailsCountryIndiaRegionWestern IndiaStateMaharashtraDistrictKolhapurLS constituencyHatkanangleReservationNoneMember of Legislative Assembly14th Maharashtra Legislative AssemblyIncumbent Rajendra Patil PartyIndependent Shirol Assembly constituency is one of the 288 Vidhan Sabha (legislative assembly) constituencies in Maharashtra state in western India...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Saeculo exeunte – news · newspapers · books · scholar · JSTOR (November 2017) Saeculo exeunte Encyclical of Pope Pius XIISignature date 13 June 1940SubjectOn the Eighth Century of the Independence of PortugalNumber3 of 41 of the pontificateTextIn...

US/UK intelligence-gathering operation This article is about the joint CIA/SIS operation. For the Australian Defence Force unit, see Joint Task Force Gold. Soviet officer inside the tunnel Operation Gold (also known as Operation Stopwatch by the British) was a joint operation conducted by the American Central Intelligence Agency (CIA) and the British MI6 Secret Intelligence Service (SIS) in the 1950s to tap into landline communication of the Soviet Army headquarters in Berlin using a tunnel i...

Koordinat: 53°47′49″N 1°32′42″W / 53.797°N 1.545°W / 53.797; -1.545 Pintu masuk Leeds Shopping Plaza Leeds Shopping Plaza merupakan pusat perbelanjaan di Leeds, Inggris dikelilingi oleh jalan-jalan di Bond Street, Albion Street, Boar Lane dan Lower Basinghall Street. Dibuka pada tahun 1977 sebagai Bond Street Centre, di lokasi sebelumnya ditempati oleh bangunan era Victoria dan diperbaharui pada tahun 1996 sekaligus mengubah namanya seperti sekarang, memper...

American retired soccer player Alecko Eskandarian Eskandarian in 2009Personal informationFull name Alecko EskandarianDate of birth (1982-07-09) July 9, 1982 (age 41)Place of birth Montvale, New Jersey, U.S.Height 5 ft 9 in (1.75 m)Position(s) ForwardCollege careerYears Team Apps (Gls)2000–2002 Virginia Cavaliers 60 (50)Senior career*Years Team Apps (Gls)2003–2006 D.C. United 81 (20)2007 Toronto FC 6 (1)2007 Real Salt Lake 17 (1)2008–2009 Chivas USA 18 (6)2009–2010 ...

Official fiat currency of South Africa South African rand List 10 other official names: Suid-Afrikaanse rand (Afrikaans) iRanti yeSewula Afrika (Southern Ndebele) iRanti yoMzantsi Afrika (Xhosa) iRandi laseNingizimu Afrika (Zulu) liRandi laseNingizimu Afrika (Swazi) Ranta ya Afrika Borwa (Northern Sotho) Ranta ya Afrika Borwa (Sotho) Ranta ya Aforika Borwa (Tswana) Rhandi ya Afrika-Dzonga (Tsonga) Rannda ya Afurika Tshipembe (Venda) ISO 4217Co...

BBC radio programme This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: You and Yours – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove this message) Radio show You and YoursOther namesYou & YoursGenreConsumer affairsRunning time53 minutesCountry of originUnited King...

British record label Virgin EMI RecordsParent companyUniversal Music Group[1]Founded2013; 11 years ago (2013) (as Virgin EMI Records)StatusDormant & Rebranded as EMI Records and Virgin RecordsDistributor(s)Self-released (UK)Republic Records (US)Def Jam Recordings (US)Capitol Records (US)Virgin Records America (US)UMe (reissues)Country of originUnited KingdomLocationLondon, EnglandOfficial websiteemirecords.com Virgin EMI Records was a British record label owned b...

Uang kertas 100 dolar Australia (Belakang) Uang kertas 100 dolar Australia (A$100) adalah nilai uang kertas yang pertama kali dikeluarkan oleh Reserve Bank of Australia pada tahun 1984 akibat inflasi. Uang kertas ini menampilkan potret di Dame Nellie Melba dan Sir John Monash. Referensi Ian W. Pitt, ed. (2000). Renniks Australian Coin and Banknote Values (edisi ke-19). Chippendale, N.S.W.: Renniks Publications. hlm. 171–172. ISBN 0-9585574-4-6. lbsMata uang AustraliaTopik Re...

London bus route 133Transport UK London Bus Wright StreetDeck Electroliner BEV on London BridgeOverviewOperatorTransport UK London BusGarageBatterseaVehicleNew RoutemasterWright StreetDeck Electroliner BEVPeak vehicle requirement25Began service27 March 1929PredecessorsRoute 34Former operator(s)Arriva LondonGo-Ahead LondonNight-timeN133RouteStartStreatham stationViaBrixtonKenningtonElephant and CastleBoroughLondon BridgeHolborn ViaductEndHolborn stationLength8 miles (13 km)ServiceLevelDai...

For related races, see 1928 United States Senate elections. 1928 United States Senate election in Maryland ← 1922 November 5, 1928 1934 → Nominee Phillips Lee Goldsborough William Cabell Bruce Party Republican Democratic Popular vote 256,224 214,447 Percentage 54.05% 45.24% County resultsGoldsborough: 50–60% 60–70% 70–80%Bruce: 50–6...

Ancient Egyptian deity This article is about the ancient Egyptian deity. For other uses, see Apep (disambiguation). ApepA depiction of Apep based on the depiction in the tomb of Ramesses I.Name in hieroglyphs [1][2]AbodeDuatSymbolSnakeTextsSpells of Coming Forth by DayGenealogyParentsNone, Neith (in some myths)SiblingsRa[dubious – discuss] Part of a series onAncient Egyptian religion Beliefs Afterlife Cosmology Duat Ma'at Mythology Index Numerology Philosophy...









![{\displaystyle [0,k\cdot n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28a374971d303529081743d2acecafe5c237265e)





















