PROFILPELAJAR.COM

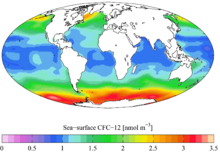
The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774–1825) of Leipzig in 1805. It was reinvented and popularized in 1857 by Jacques Babinet, who gave it the name homalographic projection. The variation homolographic arose from frequent nineteenth-century usage in star atlases.^[1]

Properties

The Mollweide is a pseudocylindrical projection in which the equator is represented as a straight horizontal line perpendicular to a central meridian that is one-half the equator's length. The other parallels compress near the poles, while the other meridians are equally spaced at the equator. The meridians at 90 degrees east and west form a perfect circle, and the whole earth is depicted in a proportional 2:1 ellipse. The proportion of the area of the ellipse between any given parallel and the equator is the same as the proportion of the area on the globe between that parallel and the equator, but at the expense of shape distortion, which is significant at the perimeter of the ellipse, although not as severe as in the sinusoidal projection.

Shape distortion may be diminished by using an interrupted version. A sinusoidal interrupted Mollweide projection discards the central meridian in favor of alternating half-meridians which terminate at right angles to the equator. This has the effect of dividing the globe into lobes. In contrast, a parallel interrupted Mollweide projection uses multiple disjoint central meridians, giving the effect of multiple ellipses joined at the equator. More rarely, the projection can be drawn obliquely to shift the areas of distortion to the oceans, allowing the continents to remain truer to form.

The Mollweide, or its properties, has inspired the creation of several other projections, including the Goode's homolosine, van der Grinten and the Boggs eumorphic.^[4]

Mathematical formulation

The projection transforms from latitude and longitude to map coordinates x and y via the following equations:^[5]

{\begin{aligned}x&=R{\frac {2{\sqrt {2}}}{\pi }}\left(\lambda -\lambda _{0}\right)\cos \theta ,\\[5px]y&=R{\sqrt {2}}\sin \theta ,\end{aligned}}

where θ is an auxiliary angle defined by

2\theta +\sin 2\theta =\pi \sin \varphi \qquad (1)

and λ is the longitude, λ₀ is the central meridian, φ is the latitude, and R is the radius of the globe to be projected. The map has area 4 $π$ R², conforming to the surface area of the generating globe. The x-coordinate has a range of [−2R√2, 2R√2], and the y-coordinate has a range of [−R√2, R√2].

Equation (1) may be solved with rapid convergence (but slow near the poles) using Newton–Raphson iteration:^[5]

{\begin{aligned}\theta _{0}&=\varphi ,\\\theta _{n+1}&=\theta _{n}-{\frac {2\theta _{n}+\sin 2\theta _{n}-\pi \sin \varphi }{2+2\cos 2\theta _{n}}}.\end{aligned}}

^{[note 1]}

If φ = ±⁠ $π$ /2⁠, then also θ = ±⁠ $π$ /2⁠. In that case the iteration should be bypassed; otherwise, division by zero may result.

There exists a closed-form inverse transformation:^[5]

{\begin{aligned}\varphi &=\arcsin {\frac {2\theta +\sin 2\theta }{\pi }},\\[5px]\lambda &=\lambda _{0}+{\frac {\pi x}{2R{\sqrt {2}}\cos \theta }},\end{aligned}}

where θ can be found by the relation

\theta =\arcsin {\frac {y}{R{\sqrt {2}}}}.\,

The inverse transformations allow one to find the latitude and longitude corresponding to the map coordinates x and y.

Alterations

Allen K. Philbrick (1953) Sinu-Mollweide uninterrupted projection, with Tissot indicatrices

Notes

^ The formula in the text helps the reader confirm that the formula is correct. For numerical computation the denominator should be changed, starting with the double angle identity.
${\begin{aligned}\cos 2\theta _{n}&=2\cos ^{2}\theta _{n}-1,\\1+\cos 2\theta _{n}&=2\cos ^{2}\theta _{n},\\2+2\cos 2\theta _{n}&=4\cos ^{2}\theta _{n},\\\theta _{n+1}&=\theta _{n}-{\frac {2\theta _{n}+\sin 2\theta _{n}-\pi \sin \varphi }{4\cos ^{2}\theta _{n}}}.\end{aligned}}$
In numerical computation, the original denominator could result in zero for θ near ±⁠ $π$ /2⁠ (catastrophic cancellation). This substitution is true for all angles and avoids the problem near θ = ±⁠ $π$ /2⁠ without making it a special case.

References

^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 112–113, ISBN 0-226-76747-7.
^ Gannon, Megan (December 21, 2012). "New 'Baby Picture' of Universe Unveiled". Space.com. Retrieved December 21, 2012.
^ Bennett, C.L.; Larson, L.; Weiland, J.L.; Jarosk, N.; Hinshaw, N.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; Komatsu, E.; Nolta, M.R.; Page, L.; Spergel, D.N.; Wollack, E.; Dunkley, J.; Kogut, A.; Limon, M.; Meyer, S.S.; Tucker, G.S.; Wright, E.L. (2013). "Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
^ Map Projections – A Working Manual, USGS Professional Paper 1395, John P. Snyder, 1987, pp. 249–252
^ ^a ^b ^c Weisstein, Eric W. "Mollweide Projection". MathWorld.