Minimax approximation algorithm
|
Read other articles:

Pallazo Piccolomini, Pienza Taman Boboli, Florence Taman Italia adalah jenis taman yang merefleksikan pemikiran Renaissance. Arsitektur Taman Italia mencapai masa keemasan pada abad ke-16.[1] Taman Italia awalnya berkembang sejak abad pertengahan bersamaan dengan meningkatnya aktivitas berkebun, dimana Kota-kota di Italia utara dan sekitar Florence mulai dihiasi dengan villa dan taman bunga mawar.[1] Di Florence, seni Renaissance dimulai saat Brunelleschi (1377-1446) mulai mem...
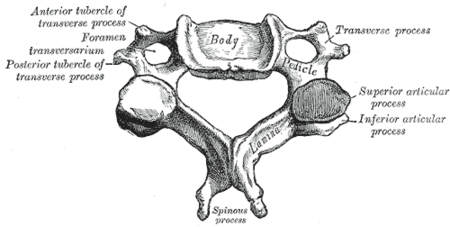
Tulang leherPosisi tulang leher pada manusia (merah) terdiri dari 7 tulang.Penampang tulang leher manusiaRincianPengidentifikasiBahasa Latinvertebrae cervicalesMeSHD002574TA98A02.2.02.001TA21032FMA9915Daftar istilah anatomi tulang[sunting di Wikidata] Pada vertebrata, Tulang leher (Latin: vertebrae cervicalescode: la is deprecated ) adalah tulang belakang yang langsung terhubung dengan tengkorak. Artikel bertopik biologi ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan men...

Halaman ini berisi artikel tentang kota. Untuk kabupaten bernama sama, lihat Tegal. Kota Tegal TagalKotaTranskripsi bahasa daerah • Hanacarakaꦠꦼꦒꦭ꧀ • Pegonتٓڮل • Hanzi直葛 • BelandaTagalDari atas searah jarum jam: Monumen Bahari, Stasiun Tegal, Monumen Yos Sudarso, dan Pacific Mall BenderaLambangJulukan: Kota BahariKota WartegPetaKota TegalPetaTampilkan peta JawaKota TegalKota Tegal (Indonesia)Tampilkan peta IndonesiaKo...

Cacia cretifera Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lamiinae Tribus: Mesosini Genus: Cacia Spesies: Cacia cretifera Cacia cretifera adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Cacia, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

How one process influences another For other uses, see Causality (disambiguation). Not to be confused with Casualty. Cause and Cause and effect redirect here. For other uses, see Cause (disambiguation) and Cause and effect (disambiguation). Causality is an influence by which one event, process, state, or object (a cause) contributes to the production of another event, process, state, or object (an effect) where the cause is partly responsible for the effect, and the effect is partly dependent...

1968 European Indoor GamesTrack events50 mmenwomen400 mmenwomen800 mmenwomen1500 mmen3000 mmen50 m hurdlesmenwomen4 × 182 m relaywomen4 × 364 m relaymenMedley relaymenwomen3 × 1000 m relaymenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenvte The men's pole vault event at the 1968 European Indoor Games was held on 10 March in Madrid.[1][2] Results Rank Name Nationality Result Notes Wolfgang Nordwig East Germany 5.20 Hennadiy B...

American journalist, born 1943 Edith LedererLederer in 2016Born1943 (age 80–81)NationalityAmericanOther namesEdie LedererEducationCornell University (BS)Stanford University (MA)OccupationJournalist Edith Lederer, also known as Edie Lederer (born 1943) is an American war journalist.[1] Early life and education Lederer grew up in Long Island. In 1963, Lederer received a Bachelor of Science degree from Cornell University and Master of Arts in communications from Stanford ...

钱塘区 (Distrik Qiantang)杭州钱塘新区Distrik Baru Qiantang Hangzhou杭州经济技术开发区Distrik Zona Pengembangan Ekonomidan Teknologi HangzhouDistrikLokasi Distrik Baru Qiantang di Hangzhou, 2020NegaraRepublik Rakyat TiongkokProvinsiZhejiangKota subprovinsiHangzhouZona waktuUTC+8 (Waktu Standar Tiongkok) Distrik Qiantang (Hanzi sederhana: 钱塘区; Hanzi tradisional: 錢塘區; Pinyin: Qiántáng qū) adalah salah satu dari sepuluh distrik perkotaan di kota seting...

1983 Indian filmSandhippuTheatrical release posterDirected byC. V. RajendranScreenplay byPeter SelvakumarStory byKader KhanPrayag RajK.K. ShuklaProduced bySanthi NarayanasamyStarringSivaji GanesanRadhaSrideviPrabhuCinematographyG. Or. NathanEdited byB. KandhasamyMusic byM. S. ViswanathanProductioncompanySivaji ProductionsRelease date 16 June 1983 (1983-06-16) CountryIndiaLanguageTamil Sandhippu (transl. Rendezvous) is a 1983 Indian Tamil-language masala film, directed by...

内華達州 美國联邦州State of Nevada 州旗州徽綽號:產銀之州、起戰之州地图中高亮部分为内華達州坐标:35°N-42°N, 114°W-120°W国家 美國建州前內華達领地加入聯邦1864年10月31日(第36个加入联邦)首府卡森城最大城市拉斯维加斯政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])喬·隆巴爾多(R斯塔...

Disambiguazione – Se stai cercando altri significati, vedi Benjamin Constant (disambigua). Benjamin ConstantBenjamin Constant Dati generaliTitolo di studioLaurea in lettere ProfessioneScrittoreSaggista Henri-Benjamin Constant de Rebecque (Losanna, 25 ottobre 1767 – Parigi, 8 dicembre 1830) è stato uno scrittore, politico, scienziato politico, nobile ed intellettuale francese di origine svizzera. Indice 1 Biografia 1.1 Primi anni 1.2 Studi tra Erlangen, Edimburgo e Parigi 1.3 S...

拉米兹·阿利雅Ramiz Alia第1任阿尔巴尼亚總統任期1991年4月30日—1992年4月9日继任萨利·贝里沙阿尔巴尼亚人民议会主席团主席任期1982年11月22日—1991年4月30日前任哈奇·列希继任转任总统阿尔巴尼亚劳动党第一书记任期1985年4月13日—1991年5月4日前任恩维尔·霍查继任无(政党解散) 个人资料出生(1925-10-18)1925年10月18日 阿尔巴尼亚斯库台逝世2011年10月17日(2011歲—10—17)(85�...

1814 battle during the War of the Sixth Coalition This article is about the battle fought in 1814. For other uses, see Battle of Reims. Battle of Reims (1814)Part of the Campaign of France of the Sixth CoalitionThe Last Victory, by Maurice OrangeDate12–13 March 1814[1]LocationReims, French Empire49°15′46″N 4°02′05″E / 49.2628°N 4.0347°E / 49.2628; 4.0347Result French victory[1]Belligerents France Russia PrussiaCommanders and leaders Napole...

Head of government of Romania Prime Minister of the Government of RomaniaPrim-ministrul Guvernului RomânieiStandard of the prime minister of RomaniaIncumbentMarcel Ciolacusince 15 June 2023StyleHis/Her ExcellencyMember ofGovernment of RomaniaSupreme Council of National DefenceSeatVictoria Palace, BucharestAppointerPresident of RomaniaTerm length4 yearsNo term limitInaugural holderBarbu Catargiu as President of The Council of MinistersFormation22 January 1862; 162 years ago&...

This is an archive of past discussions. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. Archive 20 ← Archive 22 Archive 23 Archive 24 Archive 25 Archive 26 Feedback request: All RFCs request for comment Your feedback is requested at Wikipedia:Reliable sources/Noticeboard on a All RFCs request for comment. Thank you for helping out!You were randomly selected to receive this invitation from the lis...

陸上自衛隊で用いられている予備自衛官標旗[1] 予備自衛官(よびじえいかん、英: Reserve Self-Defense Official)は、自衛隊(陸上・海上・航空)が予備要員として任用している非常勤の自衛官のこと及びその官名である。特に予備自衛官の官職または官職にある者をいう。非常勤特別職国家公務員として、有事・訓練等の際に招集され、自衛隊における各任務に就け...

Teaching position at the University of Cambridge The Bertrand Russell Professorship of Philosophy is the senior professorship in philosophy at the University of Cambridge.[1] It was established in 1896 and named the Bertrand Russell Professorship of Philosophy in 2010, after a successful fundraising appeal to endow the post.[1] The incumbent Bertrand Russell Professor is Alexander Bird, who succeeded Huw Price in October 2020.[2] Holders James Ward (1896–1925) G. E. ...

Contea di BaileyconteaLocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoMuleshoe TerritorioCoordinatedel capoluogo34°04′12″N 102°49′48″W34°04′12″N, 102°49′48″W (Contea di Bailey) Superficie2 143 km² Abitanti7 165[1] (2010) Densità3,34 ab./km² Altre informazioniFuso orarioUTC-6 CartografiaMuleshoe Contea di Bailey – Mappa Sito istituzionaleModifica dati su Wikidata · Manuale La contea di Bailey (in ingl...

Government of Finland (1924) Politics of Finland State Constitution Declaration of Independence Human rights Law enforcement Military Executive President (list) Alexander Stubb Prime Minister (list) Petteri Orpo Government Ministries (list) Legislative Parliament Speaker: Jussi Halla-aho Judiciary General Courts Supreme Court Courts of Appeal District Courts Administrative Courts Supreme Administrative Court Regional Administrative Courts Prosecutor General Chancellor of Justice Recent electi...

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


