Read other articles:

Sezione di una marmitta catalitica per autoveicoli tipicamente urbani Questa voce o sezione sull'argomento ingegneria non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. In ingegneria meccanica il convertitore catalitico, conosciuto come marmitta catalitica, è un dispositivo catalizzatore montato sull'impiant...

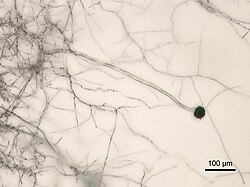
Eurotiomycetes Aspergillus niger TaksonomiSuperkerajaanEukaryotaKerajaanFungiSubkerajaanDikaryaDivisiAscomycotaSubdivisiPezizomycotinaKelasEurotiomycetes O.E.Erikss. dan Winka, 1997 Upakelas/Ordo Chaetothyriomycetidae Chaetothyriales Pyrenulales Verrucariales Eurotiomycetidae Coryneliales Eurotiales Onygenales Mycocaliciomycetidae Mycocaliciales lbs Eurotiomycetes adalah kelas dari ascomycota dalam upafilum Pezizomycotina . Beberapa anggota Eurotiomycetes sebelumnya dikelompokkan dalam kelas ...

Lima solaReformasi Protestan Sola scriptura Sola fide Sola gratia Solus Christus Soli Deo glorialbs Martin Luther: pencetus pandangan Sola Fide Justificatio sola fide (atau hanya sola fide), berarti pembenaran hanya oleh iman, adalah sebuah doktrin soteriologis dalam teologi Kristen yang umumnya dipegang untuk membedakan tradisi Lutheran and Reformed Protestan,[1] dari gereja-gereja Katolik, Ortodoks Timur, Ortodoks Oriental, Assyria and Anabaptis.[2][3] Doktrin ini me...

LDRSutradaraGuntur SoeharjantoProduser Yoen K Ody Mulya Hidayat Ditulis olehCassandra MassardiPemeranAl GhazaliVerrell BramastaMentari De MarelleAurelie MoeremansLuthya SuriPenata musikJoseph S. DjafarSinematograferEnggar BudionoPenyuntingRyan PurwokoDistributorMaxima PicturesTanggal rilis13 Mei 2015Durasi90 MenitNegara Indonesia LDR merupakan sebuah film drama Indonesia yang dirilis 13 Mei 2015. Film yang disutradarai oleh Guntur Soeharjanto. Sinopsis Impian Carrie (Mentari De Mar...

Governing body of basketball in South Korea Korea Basketball AssociationAbbreviationKBAFormation1925HeadquartersSeoulRegion served  South KoreaOfficial language KoreanPresidentPang YulParent organizationKOCWebsitewww.koreabasketball.or.kr The Korea Basketball Association (KBA; Korean: 대한농구협회) is the governing body of basketball in South Korea. Formed in 1925, it is based in Seoul. The KBA is a member of the International Basketball Federation (FIBA) and FIBA Asia. The current...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Artikel ini bukan mengenai Max Shreck. Max Schreck1922 atau sebelumnyaLahirFriedrich Gustav Maximilian Schreck6 September 1879Berlin, Kekaisaran JermanMeninggal20 Februari 1936 (usia 56)Munich, JermanSebab meninggalSerangan jantungSuami/istriFanny Normann (1910–1936) Friedrich Gustav Maximilian Schreck[1] (6 September 1879 – 20 February 1936)[2][3] adalah seorang aktor Jerman. Ia paling sering diingat saat ini karena perannya sebagai Count Orlok dalam film Nos...

 烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/（英文） 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表（英语：Representatives of the President of Ukraine） 总...

Northwich Victoria playing against Premier League side Sunderland at the Stadium of Light in the Third Round of the FA Cup on 7 January 2006. Northwich Victoria Football Club are an English football club based in Northwich, Cheshire. They are currently competing in the Northern Premier League Premier Division.[1] The club was founded in 1874, playing challenge matches organised on an ad hoc basis until the 1877 season, when they entered the Welsh Cup for the first time.[2] Th...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Papua merupakan salah satu pulau yang ada di Indonesia yang terletak di bagian Timur, yang memiliki ibukota Jayapura. Provinsi Papua bisa dikatakan sebagai salah satu provinsi terkaya di Indonesia dan memiliki luas wilayah hampir 3 kali luas wilayah Pu...

Township in Illinois, United StatesUrsa TownshipTownshipLocation in Adams CountyAdams County's location in IllinoisCoordinates: 40°04′55″N 91°24′24″W / 40.08194°N 91.40667°W / 40.08194; -91.40667CountryUnited StatesStateIllinoisCountyAdamsEstablishedNovember 6, 1849Area • Total61.03 sq mi (158.1 km2) • Land57.22 sq mi (148.2 km2) • Water3.81 sq mi (9.9 km2)  6.24%Elevatio...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Distretti del Vietnam Dal punto di vista amministrativo, le province del Vietnam sono suddivise in distretti o distretti rurali (huyện), città dipendenti dalla provincia (thành phố trực thuộc tỉnh) e cittadine (thị xã), tutte suddivisioni amministrative di secondo livello. Alcune isole poco abitate hanno a volte il titolo di isola (đảo) ma in pratica si tratta sempre di distretti rurali. Le municipalità a controllo diretto, che sono allo stesso livello delle province, sono ...

لبنان في دورة الألعاب الألومبية الشتوية عام 2010. يتميز اللبنانيون بمهاراتهم في أنواع معينة من الرياضات بالنسبة للعالم العربي. فقد تفوقوا برياضات كمال الاجسام، كرة السلة، سباق السيارات وسباقات الدراجات الهوائية، السباحة والتزلج. بالإضافة لولعهم في رياضات أخرى عالمية مثل ك...

Royal Gold, Inc.Company typePublicTraded asNasdaq: RGLDS&P 400 ComponentISINUS7802871084IndustryMiningFounded1981FounderH. Stanley DempseyHeadquartersDenver, Colorado, USAKey peopleWilliam Hayes, Chairman of the BoardBill Heissenbuttel, President and CEOPaul Libner, CFO and TreasurerProductsGold Silver Lead CopperMolybdenum Cobalt ZincPotashRevenue$498.82 mil'20[1]17.9%Operating income$198.95 mil'20[1]41.4%Net income$196.3 mil'20[1]120.3%Total assets$2.766 bil...

American middle-distance runner Olivia BakerOlivia Baker at 2018 NCAA Division I Outdoor Track and Field ChampionshipsPersonal informationNationalityAmericanBorn (1996-06-12) June 12, 1996 (age 28)Home townSouth Orange, New Jersey, U.S.Height5 ft 3 in (160 cm)Weight110 lb (50 kg)SportSportTrack and fieldEvent800 metresCollege teamStanford UniversityClubAtlanta Track ClubAchievements and titlesWorld finals2022800 m,Personal bests800 m: 1:58.05 (Mona...

Barbadian writer (1934–2016) Austin ClarkeCM OOntBornAustin Ardinel Chesterfield Clarke(1934-07-26)July 26, 1934St. James, BarbadosDiedJune 26, 2016(2016-06-26) (aged 81)Toronto, Ontario, CanadaOccupation Novelist short story writer essayist NationalityBarbadian, CanadianEducationTrinity College, TorontoPeriod1960s–2016Notable worksThe Polished Hoe (2002) Austin Ardinel Chesterfield Tom Clarke, CM OOnt (July 26, 1934 – June 26, 2016),[1] was a Barbadian novelist, es...

César Sampaio Informasi pribadiNama lengkap César SampaioTanggal lahir 31 Maret 1968 (umur 56)Tempat lahir São Paulo, BrasilPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)1986-1991 Santos 1991-1994 Palmeiras 1995-1998 Yokohama Flügels 1999-2000 Palmeiras 2000-2001 Deportivo La Coruña 2001 Corinthians 2002 Kashiwa Reysol 2003-2004 Sanfrecce Hiroshima 2004 São Paulo Tim nasional1990-2000 Brasil 47 (6) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik...

Il teorema fondamentale dell'algebra asserisce che ogni polinomio in una variabile di grado n ≥ 1 {\displaystyle n\geq 1} (cioè non costante) con coefficienti complessi, del tipo a n z n + … + a 1 z + a 0 , {\displaystyle a_{n}z^{n}+\ldots +a_{1}z+a_{0},} ammette almeno una radice complessa (o zero). Equivalentemente (per definizione) il teorema asserisce che il campo dei numeri complessi è algebricamente chiuso. Dal teorema segue che un polinomio a coefficienti complessi amme...