In geometry, the Möbius–Kantor polygon is a regular complex polygon 3{3}3, 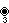

 , in
, in  . 3{3}3 has 8 vertices, and 8 edges. It is self-dual. Every vertex is shared by 3 triangular edges.[1] Coxeter named it a Möbius–Kantor polygon for sharing the complex configuration structure as the Möbius–Kantor configuration, (83).[2]
. 3{3}3 has 8 vertices, and 8 edges. It is self-dual. Every vertex is shared by 3 triangular edges.[1] Coxeter named it a Möbius–Kantor polygon for sharing the complex configuration structure as the Möbius–Kantor configuration, (83).[2]
Discovered by G.C. Shephard in 1952, he represented it as 3(24)3, with its symmetry, Coxeter called as 3[3]3, isomorphic to the binary tetrahedral group, order 24.
Coordinates
The 8 vertex coordinates of this polygon can be given in  , as:
, as:
| (ω,−1,0) |
(0,ω,−ω2) |
(ω2,−1,0) |
(−1,0,1)
|
| (−ω,0,1) |
(0,ω2,−ω) |
(−ω2,0,1) |
(1,−1,0)
|
where  .
.
As a configuration
The configuration matrix for 3{3}3 is:[3] ![{\displaystyle \left[{\begin{smallmatrix}8&3\\3&8\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37f4763f271663fad46763e02ee9eb6320ae704)
Its structure can be represented as a hypergraph, connecting 8 nodes by 8 3-node-set hyperedges.
Real representation
It has a real representation as the 16-cell, 





 , in 4-dimensional space, sharing the same 8 vertices. The 24 edges in the 16-cell are seen in the Möbius–Kantor polygon when the 8 triangular edges are drawn as 3-separate edges. The triangles are represented 2 sets of 4 red or blue outlines. The B4 projections are given in two different symmetry orientations between the two color sets.
, in 4-dimensional space, sharing the same 8 vertices. The 24 edges in the 16-cell are seen in the Möbius–Kantor polygon when the 8 triangular edges are drawn as 3-separate edges. The triangles are represented 2 sets of 4 red or blue outlines. The B4 projections are given in two different symmetry orientations between the two color sets.
The 3{3}3 polygon can be seen in a regular skew polyhedral net inside a 16-cell, with 8 vertices, 24 edges, 16 of its 32 faces. Alternate yellow triangular faces, interpreted as 3-edges, make two copies of the 3{3}3 polygon.


This graph shows the two alternated polygons as a compound in red and blue 3{3}3 in dual positions.
|

3{6}2, 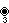   or or 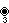  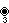 , with 24 vertices in black, and 16 3-edges colored in 2 sets of 3-edges in red and blue.[4] , with 24 vertices in black, and 16 3-edges colored in 2 sets of 3-edges in red and blue.[4]
|
It can also be seen as an alternation of 

 , represented as
, represented as 

 .
. 

 has 16 vertices, and 24 edges. A compound of two, in dual positions,
has 16 vertices, and 24 edges. A compound of two, in dual positions, 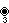

 and
and 

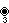 , can be represented as
, can be represented as 

 , contains all 16 vertices of
, contains all 16 vertices of 

 .
.
The truncation 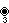

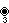 , is the same as the regular polygon, 3{6}2,
, is the same as the regular polygon, 3{6}2, 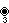

 . Its edge-diagram is the cayley diagram for 3[3]3.
. Its edge-diagram is the cayley diagram for 3[3]3.
The regular Hessian polyhedron 3{3}3{3}3, 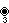



 has this polygon as a facet and vertex figure.
has this polygon as a facet and vertex figure.
Notes
- ^ Coxeter and Shephard, 1991, p.30 and p.47
- ^ Coxeter and Shephard, 1992
- ^ Coxeter, Complex Regular polytopes, p.117, 132
- ^ Coxeter, Regular Complex Polytopes, p. 109
References
- Shephard, G.C.; Regular complex polytopes, Proc. London math. Soc. Series 3, Vol 2, (1952), pp 82–97.
- Coxeter, H. S. M. and Moser, W. O. J.; Generators and Relations for Discrete Groups (1965), esp pp 67–80.
- Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974), second edition (1991).
- Coxeter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244 [1]