Lindelöf space
|
Read other articles:

Harold KrotoLahir7 Oktober 1939 (umur 84)Wisbech, Cambridgeshire, InggrisKebangsaanBritania RayaAlmamaterUniversitas SheffieldDikenal atasbuckminsterfullerenePenghargaanPenghargaan Nobel dalam Kimia tahun 1996Karier ilmiahBidangKimia Sir Harold Walter Harry Kroto FRS (lahir 7 Oktober 1939 sebagai Harold Krotoschiner) ialah seorang kimiawan Inggris berdarah Polandia-Jerman dan salah satu dari 3 tokoh yang memenangkan Penghargaan Nobel Kimia pada tahun 1996. Pendidikan dan karier 1947 - 5...

Vladislav Surkov Wakil Perdana Menteri Rusia — Kepala Kantor Eksekutif PemerintahMasa jabatan21 Mei 2012 – 8 Mei 2013Wakil Perdana Menteri RusiaMasa jabatan27 Desember 2011 – 21 Mei 2012Wakil Pertama Kepala Staf Pemerintahan Kepresidenan RusiaMasa jabatan15 Mei 2008 – 27 Desember 2011Wakil Kepala Staf Pemerintahan Kepresidenan RusiaMasa jabatan3 Agustus 1999 – 12 Mei 2008 Informasi pribadiLahirVladislav Yuryevich SurkovВладислав Юрье�...

Oscars dan The Oscar dialihkan ke halaman ini. Untuk other uses, lihat Oscar. Academy AwardsPenghargaan terkini: Academy Awards ke-96Patung Academy Award (Oscar)Diberikan kepadaPrestasi dalam industri film Amerika dan InternasionalNegaraAmerika SerikatDipersembahkan olehAcademy of Motion Picture Arts and SciencesDiberikan perdana16 Mei 1929; 94 tahun lalu (1929-05-16)Situs webwww.oscars.org/oscarsSiaran televisi/radioSaluranDaftar penyiar Academy Award atau disebut juga piala Oscar adala...

Halaman ini berisi artikel tentang warna. Untuk tumbuhan, lihat Kuma-kuma. Kuning Cempaka Bubuk kuma-kuma Koordinat warnaTriplet hex#F4C430sRGBB (r, g, b)(244, 196, 48)CMYKH (c, m, y, k)(4, 23, 81, 5)HSV (h, s, v)(45°, 80%, 96%)SumberMaerz dan Paul[1]B: Dinormalkan ke [0–255] (bita)H: Dinormalkan ke [0–100] (ratusan) Kuning cempaka atau Kurkuma (Inggris: Saffron yellowcode: en is deprecated ) adalah warna yang menyer...

Prof. dr.Jurnalis UddinPAK.Lahir10 Juli 1937 (umur 86)Sulit Air, Solok, Sumatera Barat, Hindia BelandaKebangsaanIndonesiaAlmamaterUniversitas Gadjah MadaUniversitas IndonesiaPekerjaanAhli kesehatan, pengajarDikenal atasPendiri Yayasan YARSISuami/istriZoraida Jurnalis Jurnalis Uddin (lahir 10 Juli 1937) adalah seorang ahli kesehatan dan pengajar Indonesia. Ia bersama beberapa orang koleganya, seperti Asri Rasad, merupakan pendiri Yayasan YARSI yang mengelola beberapa lembaga pendidikan d...

Penobatan George V dan MaryRaja dan Ratu dalam jubah penobatan, potret resmi penobatan oleh Emery WalkerTanggal22 Juni 1911 (1911-06-22)LokasiWestminster Abbey, London, EnglandPeserta/Pihak terlibat Raja George V Ratu Mary Pejabat Besar Negara Uskup Agung dan asisten uskup dari Gereja Inggris Garter Principal King of Arms Penobatan George V dan istrinya Mary sebagai Raja dan Ratu dari Britania Raya dan Dominion Britania Raya. Penobatan ini sekaligus sebagai penobatan Kaisar dan Permaisur...

This is a list of lists of websites, sorted by type and subject, including comparisons and other lists of lists. By type Academic databases and search engines BitTorrent (comparison) Blogs Chat Databases Dating (comparison) Dictionaries Encyclopedias Forums Notorious markets Photo sharing Question-and-answer Satirical Search engines Social bookmarking Social networking Defunct social networking Tor onion services Video platforms Webcomics Web directories Wikis By subject Biology Biodiversity...

Service agency that provides temporary residence for homeless people The examples and perspective in this article deal primarily with the United States and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (January 2019) (Learn how and when to remove this template message) The Peachtree-Pine shelter in Atlanta, Georgia, US Homeless shelters are a type of homeless service agency which pro...

Museo diocesano Leonello Barsotti UbicazioneStato Italia LocalitàLivorno IndirizzoVia del Seminario 61 Coordinate43°33′13.61″N 10°19′04.22″E / 43.553781°N 10.317839°E43.553781; 10.317839Coordinate: 43°33′13.61″N 10°19′04.22″E / 43.553781°N 10.317839°E43.553781; 10.317839 CaratteristicheTipoArte Istituzione2008 Visitatori300 (2019) e (2022) Sito web Modifica dati su Wikidata · Manuale Il Museo diocesano Leonello Barsotti è un...

Helen DahmHelen Dahm en Inde, 1938BiographieNaissance 21 mai 1878Egelshofen (d)Décès 24 mai 1968 (à 90 ans)MännedorfSépulture Oetwil am SeeNationalité suisseActivité PeintrePériode d'activité 1898-1968Autres informationsMouvement ExpressionnismeVue de la sépulture.modifier - modifier le code - modifier Wikidata Pour les articles homonymes, voir Dahm. Helen Dahm (ou Helene Dahm ; 21 mai 1878 à Egelshofen - 24 mai 1968 à Männedorf) est une peintre suisse expressionniste. ...

Min Ko NaingLahirPaw Oo Tun18 Oktober 1962 (umur 61)Mudon, Negara Bagian Mon, BurmaPendidikanUniversitas Seni & Sains Rangoon[1]OrganisasiFederasi Serikat Pelajar Seluruh BurmaKelompok Pelajar Generasi 88Serikat Perdamaian dan Terbuka Generasi 88Gerakan politikPemberontakan 8888Orang tuaU Thet Nyunt, Daw Hla Kyi[1]PenghargaanPenghargaan Gwangju untuk Hak Asasi Manusia (2009)Civil Courage Prize (2005)John Humphrey Freedom Award (1999)Bintang Jasa Nasional (2015)[2...

Men's prison in London, England HMP WandsworthLocationWandsworth,London, SW18Security classAdult Male/Category B LocalPopulation1,562Opened1851; 173 years ago (1851)Managed byHM Prison ServicesGovernorKatie Price[1]WebsiteWandsworth at justice.gov.uk HM Prison Wandsworth is a Category B men's prison at Wandsworth in the London Borough of Wandsworth, South West London, England. It is operated by His Majesty's Prison Service and is one of the largest prisons in the UK....

Not to be confused with Stratford, Connecticut; Stafford, Connecticut; or Stanford, California. City in Connecticut, United StatesStamfordCityClockwise, from top: Downtown Stamford, Harbor Point, Stamford Museum & Nature Center, Stamford Center for the Arts, Fish Church, One Stamford Forum, Stamford Transportation Center, Old Town Hall, One Landmark Square FlagSealNickname(s): The City That Works, Lock CityMotto: Innovating Since 1641 Fairfield County and Connecticut W...

Greek Civil War clashes This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dekemvriana – news · newspapers · books · scholar · JSTOR (April 2013) (Learn how and when to remove this message) DekemvrianaPart of the Greek Civil WarA Sherman tank and troops from the 5th (Scottish) Parachute Battalion, British 2nd P...

For the Australian band, see Icehouse (band).For the song featured in the album, see Icehouse (song). 1980 studio album by FlowersIcehouse1980 Australian release (Regular Records)Studio album by FlowersReleased10 October 1980 (1980-10-10)RecordedJanuary 1980StudioStudios 301 (Sydney), Paradise (Sydney)GenreNew waveLength41:5037:24Label Regular Chrysalis Warner Music Producer Cameron Allan Iva Davies Flowers chronology Icehouse(1980) Primitive Man(1982) Singles from Iceh...

Université de SheffieldHistoireFondation 19051897 University College of SheffieldStatutType Université publiqueNom officiel University of SheffieldRégime linguistique AnglaisPrésident Sir Peter MiddletonDevise Rerum cognoscere causas[1]Membre de Red brick university, Russell GroupSite web www.sheffield.ac.ukChiffres-clésÉtudiants Environ 25 700LocalisationPays Royaume-UniVille Sheffield Géolocalisation sur la carte : Angleterre Géolocalisation sur la carte : Yorkshire d...

Stasiun Shinonoi篠ノ井駅StasiunShinonoi, Desember 2008LokasiShinonoifusetakada, Nagano-shi, Nagano-ken 388-8007 JepangKoordinat36°34′40″N 138°08′16″E / 36.5777°N 138.1377°E / 36.5777; 138.1377Ketinggian356.2 meter[1]Operator JR East Shinano Railway Jalur ■Jalur Utama Shinetsu ■ Jalur Shinonoi ■ Jalur Kereta Shinano Jumlah peron1 peron sisi + 1 peron pulauInformasi lainSitus webSitus web resmiSejarahDibuka15 Agustus 1888PenumpangFY2015...

1891 short story by Robert Louis Stevenson For other uses, see The Bottle Imp (disambiguation). William Hatherell's 1905 illustration of the story; the bottle is presented to Keawe by its previous owner The Bottle Imp is an 1891 short story by the Scottish author Robert Louis Stevenson usually found in the short story collection Island Nights' Entertainments. It was first published in the New York Herald (February–March 1891) and Black and White magazine (London, March–April 1891). In it,...
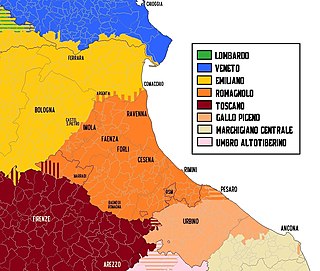
Romagnol Rumagnòl Pengucapan[rumɐˈɲoːl]/[rumɐˈɲoə̯l]Dituturkan diItalia, San MarinoWilayahUtamanya Emilia-Romagna, San Marino, MarcheEtnis1,1 juta (2008)[1]PenuturTidak diketahui, ca 430.000, diasumsikan Romagnol dan Emilia memiliki jumlah yang sama (2006)[2] Perincian data penutur Jumlah penutur beserta (jika ada) metode pengambilan, jenis, tanggal, dan tempat. 1.100.000 (2008) Rumpun bahasaIndo-Eropa ItalikLatino-FaliskiRomanItalo-BaratRoman Barat...

ESPNEWSCaractéristiquesCréation 1er novembre 1996Propriétaire The Walt Disney Company (80 %)Hearst Corporation (20 %)Langue AnglaisPays États-UnisSiège social Bristol, ConnecticutDiffusionSatellite DirecTV : 207 (SD/HD)Dish Network : 142 (SD), 5301 (HD)Câble Verizon Fios : 72 (SD), 572 (HD)IPTV mio TV (Singapour) : 116 (SD/HD)now TV (Hong Kong) : TBAmodifier - modifier le code - modifier Wikidata ESPNEWS[1] est une chaîne d'information sportive en con...

















