Laurence Waldron

Laurence Waldron

Member of Parliament for Tipperary
In office 14 April 1857 – 24 July 1865 Serving with Charles Moore (February 1865–July 1865) Daniel O'Donoghue (1857–1865)
Preceded by	Francis Scully Daniel O'Donoghue
Succeeded by	Charles Moore John Blake Dillon

Personal details
Born	1811
Died	3 April 1875 (aged 63)
Nationality	Irish
Political party	Liberal
Other political affiliations	Whig
Spouse	Anne White
Children	Laurence Ambrose Waldron

Laurence Waldron (1811 – 3 April 1875)^[1] was an Irish Independent Liberal, Liberal and Whig politician. He sat in the House of Commons of the United Kingdom from 1857 to 1865 as one of the two Members of Parliament (MPs) for Tipperary.

Waldron married Anne White, daughter of Francis White.^[2] He had at least one son, Laurence Ambrose Waldron, who was an Irish Parliamentary Party MP for Dublin St Stephen's Green from 1904 to 1910.^[3]

Waldron first stood for Parliament as a Whig at a by-election in Tipperary, caused by the expulsion of James Sadleir from the House of Commons.^[4] Unsuccessful on this occasion, he was elected as a Whig for the same seat just a month later at the 1857 general election, holding the seat — standing as a Liberal in 1859 — until he stood down in 1865. Upon the death of John Blake Dillon in 1866, he stood for the seat again, this time as an Independent Liberal, but was unsuccessful.^[5]^[6]

He was also at some point a Deputy Lieutenant.^[2]

References

^ Leigh Rayment's Historical List of MPs – Constituencies beginning with "T" (part 1)
^ ^a ^b "20". History of the RSCI (PDF). p. 453.
^ "The Political Journal of Sir George Fottrell". Camden. Fifth Series. 33: 81–198. December 2008. doi:10.1017/S0960116308003242.
^ "County Tipperary Election". Waterford News. 13 March 1857. p. 4. Retrieved 19 March 2018 – via British Newspaper Archive.
^ "Mr. Waldron's Candidature". Dublin Evening Mail. 2 October 1866. p. 4. Retrieved 19 March 2018 – via British Newspaper Archive.
^ Walker, B.M., ed. (1978). Parliamentary Election Results in Ireland, 1801–1922. Dublin: Royal Irish Academy. ISBN 0901714127.

External links

Hansard 1803–2005: contributions in Parliament by Mr Laurence Waldron

Parliament of the United Kingdom
Preceded by Francis Scully Daniel O'Donoghue	Member of Parliament for Tipperary 1857 – 1865 With: Charles Moore (February 1865–July 1865) Daniel O'Donoghue (1857–1865)	Succeeded by Charles Moore John Blake Dillon

This article about a Liberal Member of the Parliament of the United Kingdom is a stub. You can help Wikipedia by expanding it.

This article about a Member of the Parliament of the United Kingdom, for a constituency in Ireland between 1801 and 1922 is a stub. You can help Wikipedia by expanding it.

Read other articles:

العلاقات البوسنية السنغافورية

العلاقات البوسنية السنغافورية البوسنة والهرسك سنغافورة البوسنة والهرسك سنغافورة تعديل مصدري - تعديل العلاقات البوسنية السنغافورية هي العلاقات الثنائية التي تجمع بين البوسنة والهرسك وسنغافورة.[1][2][3][4][5] مقارنة بين البلدين هذه مقارن�...

Первородный грех

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

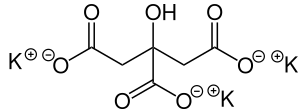
Kalium sitrat

Kalium sitrat Nama Nama IUPAC (preferensi) Trikalium 2-hidroksipropana-1,2,3-trikarboksilat Penanda Nomor CAS 866-84-2 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChEMBL ChEMBL1200458 N ChemSpider 12775 Y Nomor EC PubChem CID 13344 Nomor RTECS {{{value}}} UNII 86R1NVR0HW Y CompTox Dashboard (EPA) DTXSID8027325 InChI InChI=1S/C6H8O7.3K/c7-3(8)1-6(13,5(11)12)2-4(9)10;;;/h13H,1-2H2,(H,7,8)(H,9,10)(H,11,12);;;/q;3*+1/p-3 YKey: QEEAPRPFLLJWCF-UHFFFAOYSA-K&...

Warner Bros. Discovery

Warner Bros. Discovery, Inc.JenisPublikKode emiten Nasdaq: WBD (Series A) S&P 500 component[1] ISINUS9344231041IndustriMedia massa HiburanPendahuluWarnerMediaDiscovery, Inc.Didirikan8 April 2022; 2 tahun lalu (2022-04-08)Kantorpusat230 Park Avenue South, New York City, New York[2], Amerika SerikatWilayah operasiSeluruh duniaTokohkunci Samuel DiPiazza (Ketua) David Zaslav (Presiden dan CEO) JasaPenyiaranLisensiPenerbitanStreamingTelevisiDivisi Warner Bros. Discove...

Tomas N'evergreen

Tomas N'evergreenTomas N'evergreenBackground informationBirth nameTomas ChristiansenBorn (1969-11-12) 12 November 1969 (age 54)Hadsten, DenmarkOriginMoscow, RussiaGenresElectropop, houseOccupation(s)SingerWebsitewww.nevergreen.comMusical artist Tomas Christiansen (born 12 November 1969[1]), better known by his stage name Tomas N'evergreen,[2] is a Danish-Russian pop singer. The singles Since You've Been Gone and Everytime (I See Your Smile) were on top ten lists throughou...

イスラームにおける結婚

イスラームにおける結婚（イスラームにおけるけっこん）とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...

Bad (David Guetta and Showtek song)

2014 single by David Guetta and Showtek featuring VassyBadSingle by David Guetta and Showtek featuring Vassyfrom the album Listen Released17 March 2014 (2014-03-17)GenreBig room houseLength2:50 (radio edit)4:30 (extended mix)Label Parlophone Jack Back What a Music Songwriter(s) David Guetta Wouter Janssen Sjoerd Janssen Giorgio Tuinfort Ossama Al Sarraf Ned Shepard Manuel Reuter Vassy Nick Turpin Producer(s) David Guetta Showtek Sultan & Ned Shepard Manuel Reuter David Guet...

Prasasti Perjanjian Sunda-Portugal

Padrão Sunda Kelapa di Museum Nasional, Jakarta Prasasti Perjanjian Sunda-Portugal atau Padrão Sunda Kelapa adalah sebuah prasasti berbentuk tugu batu (padrão) yang ditemukan pada tahun 1918 di Batavia, Hindia Belanda. Prasasti ini menandai perjanjian Kerajaan Sunda–Kerajaan Portugal yang dibuat oleh utusan dagang Portugis dari Malaka yang dipimpin Enrique Leme dan membawa barang-barang untuk Raja Samian (maksudnya Sanghyang, yaitu Sang Hyang Surawisesa, pangeran yang menjadi pemimpin ut...

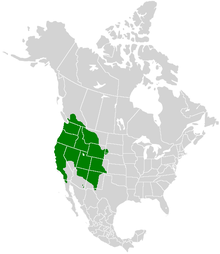
Papilio rutulus

Species of butterfly This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2020) (Learn how and when to remove this message) Papilio rutulus Papilio rutulus. Dorsal view Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Papilionidae Genus: Papilio Speci...

Loes Gunnewijk

Dutch racing cyclist Loes GunnewijkPersonal informationFull nameLoes GunnewijkBorn (1980-11-27) 27 November 1980 (age 43)Groenlo, NetherlandsTeam informationCurrent teamKNWUDisciplinesRoadRoleRider (retired)Directeur sportifCoachProfessional teams2004–2005Ondernemers van Nature2006–2009Buitenpoort-Flexpoint Team2010–2011Nederland Bloeit2012–2015GreenEDGE–AIS Managerial teams2016Orica–AIS2017–KNWU Major winsOmloop Het Nieuwsblad (2012) Medal record Representing Ori...

Tango Entertainment

American film production company Tango Productions, LLCTrade nameTango EntertainmentCompany typePrivateIndustryFilm industryFounded2017; 7 years ago (2017)Founder Lia Buman Tim Headington HeadquartersLos Angeles, California, U.S.Area servedUnited StatesWebsitetango-entertainment.com Tango Productions, LLC,[1] doing business as Tango Entertainment, is an American film production company founded in 2017 by Lia Buman and Tim Headington. The company is best known for pro...

Bedotia madagascariensis

Species of fish Bedotia madagascariensis Conservation status Endangered (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Atheriniformes Family: Melanotaeniidae Genus: Bedotia Species: B. madagascariensis Binomial name Bedotia madagascariensisRegan, 1903 Bedotia madagascariensis (zona) is a species of fish in the family Bedotiidae. It is endemic to Madagascar, where found in rivers and lakes between the...

Famille Fornier (Ariège)

Pour les articles homonymes, voir Famille Fornier. Famille Fornier Armes Blasonnement D'argent à un chevron de gueules accompagné en chef de deux croissants de même et en pointe d'une quinte feuille aussi de gueules ; au chef d'azur chargé d'un croissant d'argent accosté de deux étoiles de même[1] Branches de Garanoude Savignacde Clauzelles Période XVe siècle - XXIe siècle Pays ou province d’origine Ariège Fiefs tenus Garanou, Savignac, Clauzelles Demeures Châtea...

Mimics and Gesture Theatre

Theatre in Moscow, Russi The Mimics and Gesture Theatre is a theatre located in the Eastern Administrative Okrug of Moscow, Russia.[1] It offers special sessions for deaf people. The theatre is located in Izmailovsky bulv., 39/41 (Pervomayskaya metro station)[2] References ^ Moscow International Portal Archived 2009-09-02 at the Wayback Machine by Department of Foreign Economic and International Relations of the City of Moscow ^ Places/Theatres en Expat.ru 55°47′51″N 37°...

Novosibirsk State University of Architecture, Design and Arts

Other organization in Novosibirsk, Russia Novosibirsk State University of Architecture, Design and ArtsНовосибирский государственный университет архитектуры, дизайна и искусствTypeState UniversityEstablished1989 (1989)LocationNovosibirsk, RussiaWebsitensuada.ru Novosibirsk State University of Architecture, Design and Arts named after A. D. Kryachkov (Russian: Новосибирский государственный уни...

Casorate Sempione

Casorate Sempione komune di Italia Tempat Negara berdaulatItaliaDaerah di ItaliaLombardyProvinsi di ItaliaProvinsi Varese NegaraItalia Ibu kotaCasorate Sempione PendudukTotal5.637 (2023 )GeografiLuas wilayah6,91 km² [convert: unit tak dikenal]Ketinggian285 m Berbatasan denganArsago Seprio Cardano al Campo Gallarate Somma Lombardo SejarahSanto pelindungHilarius dari Poitiers Informasi tambahanKode pos21011 Zona waktuUTC+1 UTC+2 Kode telepon0331 ID ISTAT012039 Kode kadaster ItaliaB9...

منتخب الصين لكرة القاعدة

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

كحالة

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) كحالة الإحداثيات 33°49′19″N 35°35′15″E / 33.821944444444°N 35.5875°E / 33.821944444444; 35.5875 تقسيم إداري البل�...

Winning percentage

Sports statistic Win–loss record redirects here. For the baseball statistic, see Win–loss record (pitching). In sports, a winning percentage or Copeland score is the fraction of games or matches a team or individual has won. The statistic is commonly used in standings or rankings to compare teams or individuals. It is defined as wins divided by the total number of matches played (i.e. wins plus draws plus losses). A draw counts as a 1⁄2 win. winning percentage = wins + 0.5 ⋅ ...

Uniform tiling

Vertex-transitive tiling of the plane by regular polygons In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive. Uniform tilings can exist in both the Euclidean plane and hyperbolic plane. Uniform tilings are related to the finite uniform polyhedra; these can be considered uniform tilings of the sphere. Most uniform tilings can be made from a Wythoff construction starting with a symmetry group and a singular gener...