Klein–Kramers equation
|
Read other articles:
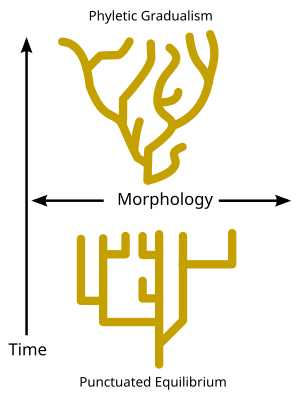
Gradualisme filetik dibandingkan dengan keseimbangan bersela (bawah). Gradualisme filetik adalah model evolusi yang menjelaskan bahwa sebagian besar spesiasi bersifat lambat, seragam, dan berangsur-angsur.[1] Seluruh spesies secara perlahan mengalami perubahan menjadi spesies yang baru. Dalam sudut pandang ini, tidak ada garis batas yang jelas antara spesies nenek moyang dengan spesies baru. Gradualisme filetik sering kali dianggap berlawanan dengan teori keseimbangan bersela, yang me...

Dewan Internasional untuk Ilmu PengetahuanInternational Council for ScienceSingkatanICSUPenerusDewan Sains InternasionalTanggal pendirian1931; 93 tahun lalu (1931)TipeLSM internasionalKantor pusatParis, PrancisPresiden Gordon McBeanSitus webICSUNama sebelumnyaDewan Internasional Persatuan Ilmiah Anggota Anggota sebagai peserta di Akademi Ilmu Pengetahuan Karibia atau Universitas Pasifik Selatan Dewan Internasional untuk Ilmu Pengetahuan (Inggris: International...

Wrestling at the Olympics Men's Greco-Roman welterweightat the Games of the XIV OlympiadVenueEmpress Hall, Earls Court Exhibition CentreDates3–6 AugustCompetitors16 from 16 nationsMedalists Gösta Andersson Sweden Miklós Szilvási Hungary Henrik Hansen Denmark← 19361952 → Wrestling at the1948 Summer OlympicsGreco-RomanFlymenBantammenFeathermenLightmenWeltermenMiddlemenLight heavymenHeavymenFreestyleFlymenBantammenFeathermenLightmenWeltermen...

العلاقات الأوزبكستانية الرواندية أوزبكستان رواندا أوزبكستان رواندا تعديل مصدري - تعديل العلاقات الأوزبكستانية الرواندية هي العلاقات الثنائية التي تجمع بين أوزبكستان ورواندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للد�...

Sepiring daging kelinci mentah Daging kelinci adalah daging yang dihasilkan dari kelinci atau terwelu. Daging ini umumnya dikonsumsi di Eropa, Benua Amerika, dan sebagian Timur Tengah. Kelinci yang dijadikan makanan dapat berupa hasil buruan maupun hasil pemeliharaan, yang disebut dengan cuniculture. Daging kelinci merupakan sumber protein yang baik dan memiliki lebih sedikit lemak dibandingkan daging sapi, daging babi, dan daging ayam.[1] Kandungan lemak kelinci hanya delapan persen,...

NSAID analgesic and anti-inflammatory drug GlucametacinClinical dataTrade namesTeoremacOther namesIndometacin glucosamideIdentifiers IUPAC name 2-[1-(4-Chlorobenzoyl)-5-methoxy-2-methylindol-3-yl]-N-[(2R,3R,4S,5R)-3,4,5,6-tetrahydroxy-1-oxohexan-2-yl]acetamide CAS Number52443-21-7PubChem CID3033980ChemSpider2298541UNIIN1EXE5EHANKEGGD08021ChEMBLChEMBL488914CompTox Dashboard (EPA)DTXSID80200445 ECHA InfoCard100.052.640 Chemical and physical dataFormulaC25H27ClN2O8Molar mass518.95 g·mol−...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Reggina Calcio. Società Sportiva La DominanteStagione 1937-1938Sport calcio Squadra Dominante R.C. Prima Divisione1º girone calabrese, (promossa Serie C) 1934-1935 1938-1939 Si invita a seguire il modello di voce Questa pagina raccoglie i dati riguardanti la So...

Talas Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monokotil Ordo: Alismatales Famili: Araceae Genus: Colocasia Spesies: C. esculenta Nama binomial Colocasia esculenta(L.) Schott[1] Sinonim Arum esculentum L., 1753[2] (basionym) Colocasia antiquorum Schott sinonim lain, lihat pada The Plant List[3] Talas, keladi, atau seratah (Colocasia esculenta L.) adalah tumbuhan penghasil umbi-umbian yang cukup penting. Tanaman ini berasal...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Bola salju – berita · surat kabar · buku · cendekiawan · JSTOR (Februari 2014) Sekumpulan bola salju Sebuah bola salju besar Bola salju adalah bernda berbentuk bola yang terbuat dari salju. Bola salju yang pa...

Pour les articles homonymes, voir Méridien (homonymie). Chaque méridien géographique part d'un pôle pour aboutir à l'autre. En géographie, un méridien est une demi-ellipse[a] imaginaire tracée sur le globe terrestre reliant les pôles géographiques[1]. Tous les points de la Terre situés sur un même méridien ont la même longitude. On parle également d'arc de méridien entre deux points ayant une latitude différente. En astronomie, un méridien est un grand cercle imaginaire tra...

1916 United States Senate election in Vermont ← 1910 November 7, 1916 (1916-11-07) 1922 → Nominee Carroll S. Page Oscar C. Miller Party Republican Democratic Popular vote 47,362 14,956 Percentage 74.41% 23.50% U.S. senator before election Carroll S. Page Republican Elected U.S. Senator Carroll S. Page Republican Elections in Vermont Federal government Presidential elections 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 ...

Questa voce sull'argomento arbitri di calcio norvegesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Dag Vidar Hafsås Informazioni personali Arbitro di Calcio Sezione Kolstad Fotball Attività nazionale Anni Campionato Ruolo 2008- Eliteserien Arbitro Attività internazionale 2012-2018 UEFA Arbitro Esordio 5 luglio 2012 Dag Vidar Hafsås (Trondheim, 26 giugno 1973) è un arbitro di calcio norvegese. Carriera Helgerud arbitrò il primo incontro nell'...

Port Vale 2012–13 football seasonPort Vale2012–13 seasonChairmanPaul Wildes(from 20 November)ManagerMicky AdamsStadiumVale ParkFootball League Two3rd (78 points)FA CupSecond Round(knocked out by Sheffield United)League CupFirst Round(knocked out by Burnley)Football League TrophyThird Round(knocked out by Bradford City)Player of the YearTom PopeTop goalscorerLeague: Tom Pope (31)All: Tom Pope (33)Highest home attendance12,496 vs. Northampton Town, 20 April 2013Lowest home attendance2,702 ...

Grand Prix Rusia 2018 Lomba ke-16 dari 21 dalam Formula Satu musim 2018← Lomba sebelumnyaLomba berikutnya → Tata Letak Sochi Autodrom.Detail perlombaan[1]Tanggal 30 September 2018Nama resmi Formula 1 2018 VTB Russian Grand PrixLokasi Sochi Autodrom,Kota Distrik Adlersky, Sochi, Krasnodar Krai, RusiaSirkuit Fasilitas balapan permanenPanjang sirkuit 5.848 km (3.634 mi)Jarak tempuh 53 putaran, 309.745 km (192.467 mi)Cuaca BerawanPosisi polePembalap Valtteri Bottas...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Battle of Sugar PointPart of the American Indian WarsOjibways in a canoe on Leech Lake, 1896.DateOctober 5, 1898LocationLeech Lake, MinnesotaResult Chippewa victoryBelligerents Chippewa United StatesCommanders and leaders Bugonaygeshig John M. Bacon Melville Wilkinson †Strength 19 warriors 500Casualties and losses none killed 7 killed (including 1 Indian Policeman shot by mistake)19 wounded vteEnd of American Indian Wars(1895–1924) Renegade period Bannock Uprising Yaqui Upr...

Dua penaklukan paling besar sepanjang abad pertengahan, Kekhalifahan Arab dan Kekaisaran Mongol. Istilah Kekuatan Besar hanya digunakan dalam historiografi dan ilmu politik sejak Kongres Wina pada tahun 1815.[1][2] Lord Castlereagh, Sekretaris Luar Negeri Inggris, pertama kali menggunakan istilah itu dalam konteks diplomatiknya pada tahun 1814 dengan mengacu pada Perjanjian Chaumont. Penggunaan istilah ini dalam historiografi Abad Pertengahan berbeda untuk masing-masing penul...

Top left: Riad Solh was the first prime minister of the Republic of Lebanon.Top right: Rashid Karami was the longest-serving prime minister of Lebanon serving for 8 terms.Bottom left: Rafic Hariri is one of the most celebrated prime minister of Lebanon and was the second longest-serving prime minister.Bottom right: Najib Mikati is the current prime minister of Lebanon in his third term. This is a list of prime ministers of Lebanon (officially titled President of the Council of Ministers) sin...

France top-level subdivision used for French Polynesia This article is part of a series on theAdministrativedivisions of France Administrative divisions Regions Departments Arrondissements Cantons Intercommunality Métropole Communauté urbaine Communauté d'agglomération Communauté de communes Communes Associated communes Municipal arrondissements Overseas France Overseas departments and regions Overseas collectivities Overseas country (French Polynesia) Sui generis collectivity (New Caled...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2009 World Championships in Athletics – Women's 4 × 100 metres relay – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) Events at the2009 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen150...








![{\displaystyle {\begin{aligned}f(x,p,t)={\frac {1}{2\pi \sigma _{X}\sigma _{P}{\sqrt {1-\beta ^{2}}}}}\exp \left(-{\frac {1}{2(1-\beta ^{2})}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}+{\frac {(p-\mu _{P})^{2}}{\sigma _{P}^{2}}}-{\frac {2\beta (x-\mu _{X})(p-\mu _{P})}{\sigma _{X}\sigma _{P}}}\right]\right),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c4eaa5cecddf24f4ce6c7156fc3134ef7a97126)
![{\displaystyle {\begin{aligned}&\sigma _{X}^{2}={\frac {k_{\mathrm {B} }T}{m\xi ^{2}}}\left[1+2\xi t-\left(2-e^{-\xi t}\right)^{2}\right];\qquad \sigma _{P}^{2}=mk_{\mathrm {B} }T\left(1-e^{-2\xi t}\right)\\[1ex]&\beta ={\frac {k_{\text{B}}T}{\xi \sigma _{X}\sigma _{P}}}\left(1-e^{-\xi t}\right)^{2}\\[1ex]&\mu _{X}=x'+(m\xi )^{-1}\left(1-e^{-\xi t}\right)p';\qquad \mu _{P}=p'e^{-\xi t}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8a0d28f383226ddbc8e6e7340c386c86840de92)

![{\displaystyle {\begin{aligned}f(\mathbf {r} ,\mathbf {p} ,t)={\frac {1}{\left(2\pi \sigma _{X}\sigma _{P}{\sqrt {1-\beta ^{2}}}\right)^{3}}}\exp \left[-{\frac {1}{2(1-\beta ^{2})}}\left({\frac {|\mathbf {r} -{\boldsymbol {\mu }}_{X}|^{2}}{\sigma _{X}^{2}}}+{\frac {|\mathbf {p} -{\boldsymbol {\mu }}_{P}|^{2}}{\sigma _{P}^{2}}}-{\frac {2\beta (\mathbf {r} -{\boldsymbol {\mu }}_{X})\cdot (\mathbf {p} -{\boldsymbol {\mu }}_{P})}{\sigma _{X}\sigma _{P}}}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34363db77509592a45b6e686a46e777233390772)







![{\displaystyle \Phi _{D}(x,t)=({\sqrt {2\pi t}}\sigma _{X}^{2})^{-1/2}\exp \left[-x^{2}/(2\sigma _{X}^{2}t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/329a581e560fa46ccc3f8dbcbc62f46fe214d8d4)

![{\displaystyle w{\frac {\partial f(z,w)}{\partial z}}={\frac {\partial }{\partial w}}\left[wf(z,w)\right]+{\frac {\partial ^{2}f(z,w)}{\partial w^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc8aa5efa0e53c5adcd613469a8bbc39e40deda)




![{\displaystyle f(x,w)={\frac {w_{0}e^{-w^{2}/2}}{\sqrt {2\pi }}}\left[w_{0}-\zeta \left({\frac {1}{2}}\right)-\sum _{n=1}^{\infty }{\frac {G_{-n}(w_{0})}{2nQ_{n}}}+\sum _{n=1}^{\infty }S_{n}(w_{0})G_{n}(w)e^{-{\sqrt {n}}z}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/515cab0ce52007a6e4c6f6c2780878bb5fa988f1)
![{\displaystyle {\begin{aligned}G_{\pm n}(w)&=(-1)^{n}2^{-n/2}e^{-n}(n!)^{-1/2}e^{\pm {\sqrt {n}}w}H_{n}\left({\frac {w}{\sqrt {2}}}\mp {\sqrt {2n}}\right),\qquad n=1,2,3,\ldots \\[1ex]S_{n}(w_{0})&={\frac {G_{n}(w_{0})}{2{\sqrt {2}}}}-{\frac {1}{2nQ_{n}}}-\sum _{m=1}^{\infty }{\frac {G_{-m}(w_{0})}{4\left(m{\sqrt {n}}+{\sqrt {m}}n\right)Q_{m}Q_{n}}}\\[2ex]Q_{n}&=\lim _{N\to \infty }{\sqrt {n!(N-1)!}}\;e^{2{\sqrt {Nn}}}\left[\prod _{r=0}^{N+n-1}\left({\sqrt {r}}+{\sqrt {n}}\right)\right]^{-1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb99f7fda4f5d1bf37291562a3769b3353412be9)