Read other articles:

American racing driver Spencer PigotPigot at the 2018 ABC Supply 500Nationality AmericanBorn (1993-09-29) September 29, 1993 (age 30)Pasadena, California, United StatesHeight5 ft 9 in (175 cm)[1]Weight162 lb (73 kg)Achievements2014 Pro Mazda Champion2015 Indy Lights ChampionIndyCar Series career57 races run over 5 yearsTeam(s)No. 45 (Rahal Letterman Lanigan Racing with Citrone/Buhl Autosport)2019 position14thBest finish14th (2018, 2019)First race2016 Fire...

Pour les articles homonymes, voir Alexandre Popov et Popov. Alexandre PopovAlexandre Popov.BiographieNaissance 4 mars 1859KrasnotourinskDécès 31 décembre 1905 (à 46 ans)Saint-PétersbourgSépulture Literatorskie mostki (d)Nationalité russeFormation Пермская духовная семинария (d)Faculté de physique et de mathématiques de l'université de Saint-Pétersbourg (d)Activités Physicien, inventeur, ingénieurAutres informationsA travaillé pour Université d'él...

Sofiane Feghouli Feghouli dengan timnas Aljazair pada 2014Informasi pribadiNama lengkap Sofiane FeghouliTanggal lahir 26 Desember 1989 (umur 34)Tempat lahir Levallois-Perret, PrancisTinggi 1,78 m (5 ft 10 in)Posisi bermain Gelandang serangInformasi klubKlub saat ini Fatih KaragümrükNomor 8Karier junior1998–2003 Red Star Paris2003–2004 Paris FC2004–2007 GrenobleKarier senior*Tahun Tim Tampil (Gol)2007–2010 Grenoble 60 (3)2010–2016 Valencia 146 (20)2011 → Alme...

Tretes beralih ke halaman ini, dengan artikel dan wilayah yang samaPrigen Daerah Wisata & Peristirahatan TretesKecamatanPrigenPeta lokasi Kecamatan PrigenTampilkan peta Surabaya dan MalangPrigenPrigen (Kabupaten Pasuruan)Tampilkan peta Kabupaten PasuruanPrigenPrigen (Provinsi Jawa Timur)Tampilkan peta Provinsi Jawa TimurPrigenPrigen (Jawa)Tampilkan peta JawaPrigenPrigen (Indonesia)Tampilkan peta IndonesiaKoordinat: 7°42′00″S 112°38′17″E / 7.7000959°S 112.6380040...

Questa voce o sezione sull'argomento elezioni non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Elezioni europee 1989 Area  Comunità europea Data 15-18 giugno 1989 Legislatura III legislatura Affluenza 58,41% ( 0,57%) Eletti 518 Europarlamentari Seggi per gruppo politico SOC 180 / 518 PPE 121 / 518 LDR 49 / 518 DE 34 / 518 GV 30 / 518 GUE 28 / 518 AD...

Michel Bastos Bastos allo Schalke 04 nel 2013 Nazionalità  Brasile Altezza 179 cm Peso 69 kg Calcio Ruolo Centrocampista, Ala Termine carriera 8 ottobre 2019 Carriera Giovanili 1994-2001 Pelotas2001-2002 Feyenoord Squadre di club1 2002-2003→  Excelsior28 (0)2003-2004 Atlético Paranaense10 (0)2004→  Grêmio19 (4)2005-2006→  Figueirense35 (10)2006-2009 Lilla97 (25)2009-2013 Olympique Lione98 (26)2013→  Schalke 0414 (4)2013-2014 A...

2022年美屬處女群島總督選舉 ← 2018 2022年11月8日 2026 → 已登記選民39910投票率21656 ▼   获提名人 阿爾伯特·布賴恩 庫爾特·維亞萊特 政党 民主党 无党籍 竞选搭档 特雷根扎·羅奇 珍妮爾·薩勞維 民選得票 12157 8244 得票率 56.14% 38.07% 按選區結果 布賴恩:      特l維亞萊特:      选前總督 阿爾伯特·布賴恩 民主黨 當選總督 阿爾伯特�...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Frisch Medal – news · newspapers · books · scholar · JSTOR (June 2014) (Learn how and when to remove this message) The Frisch Medal is an award in economics given by the Econometric Society. It is awarded every two years for empirical or theoretical applied research published in Econometrica[1] dur...

Part of a series on theCulture of Montenegro History Roman period Praevalitana Duklja Zeta under Nemanjići under Balšići under Crnojevići Venetian period Venetian Albania French period Illyrian Provinces Ottoman period Sanjak Vilayet Austrian period Venetian Province Kingdom of Dalmatia Prince-Bishopric Principality Kingdom (1910–18) Kingdom of Yugoslavia Zeta Banovina World War II Italian governorate of Montenegro German occupied territory of Montenegro CASNO SFR Yugoslavia Socialist ...

Finnish film producer and director This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Risto Orko – news · newspapers · books · scholar · JSTOR (February 2010) (Learn how and when to remove this message) Risto OrkoBornRisto Eliel William Nylund(1899-09-15)15 September 1899Rauma, FinlandDied29 September 2001(2001...

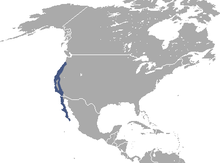
Species of mammal This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Brush rabbit – news · newspapers · books · scholar · JSTOR (January 2014) (Learn how and when to remove this message) Brush rabbit[1] Brush rabbit (Finley National Wildlife Refuge) Conservation status Least Concern  (IUCN 3.1)[...

Eccellenza 2004-2005 Competizione Eccellenza Sport Calcio Edizione 14ª Organizzatore Lega Nazionale Dilettanti Luogo  Italia Partecipanti 473 Formula 28 gironi all'italiana Cronologia della competizione 2003-2004 2005-2006 Manuale Il campionato di calcio di Eccellenza regionale 2004-2005 è stato il quattordicesimo organizzato in Italia. Rappresenta il sesto livello del calcio italiano. Il campionato è strutturato su vari gironi all'italiana su base regionale. Questo è il quadro dell...

American evolutionary biologist (1938–2011) Lynn MargulisMargulis in 2005BornLynn Petra Alexander(1938-03-05)March 5, 1938Chicago, Illinois, U.S.DiedNovember 22, 2011(2011-11-22) (aged 73)Amherst, Massachusetts, U.S.Alma materUniversity of ChicagoUniversity of Wisconsin–MadisonUniversity of California, BerkeleyKnown forSymbiogenesisGaia hypothesisSpouses Carl Sagan ​ ​(m. 1957; div. 1965)​ Thomas Margulis ​ ​&#...

Brighton & Hove redirects here. For the bus company, see Brighton & Hove (bus company). City and unitary authority in EnglandBrighton and Hove City of Brighton and HoveCity and unitary authorityClockwise, from top: the seafront; the bandstand; Falmer Stadium; the Peace Statue; Churchill SquareBrighton and Hove shown within East Sussex and EnglandBrighton and HoveLocation of Brighton and HoveShow map of the United KingdomBrighton and HoveBrighton and Hove (Europe)Show map of EuropeCoor...

Architecture of Karnataka (345 to present) Type Period Kadamba architecture – synthesis of several schools (345 to 525) Dravidian architecture (Western Ganga Dynasty) (350 to 550) Badami Chalukya architecture or the Vesara style (543 to 753) Dravidian & Rekhanagara architecture of Rashtrakutas (753 to 973) Western Chalukya architecture (Kalyani Chalukyas) (1000 and 1200) Hoysala architecture of the Hoysala Empire (1100 and 1400) Vijayanagara architecture of the Vijayanagar Empire (1336...

Curve that winds around a central point For other uses, see Spiral (disambiguation). Cutaway of a nautilus shell showing the chambers arranged in an approximately logarithmic spiral In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.[1][2][3][4] It is a subtype of whorled patterns, a broad group that also includes concentric objects. Helices An Archimedean spiral (black), a helix (green), and a c...

Evakuasi dari Afghanistan (2021)Bagian dari Setelah Kejatuhan Kabul (2021)Pengungsi dimuat ke Angkatan Udara Uni Emirat Arab Boeing C-17 Globemaster III selama evakuasi pada 20 Agustus 2021LokasiKabul, AfghanistanTujuanEvakuasi staf diplomatik, militer dan sipil internasional, termasuk warga sipil nasionalTanggal15 Agustus 2021 –Pelaksana Australia Austria[1] Belgia Kanada (Operation AEGIS) Ceko[2] Denmark Finlandia Prancis (Operat...

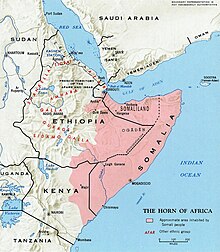
Tiếng SomaliAf-Soomaali   /   اف سومالى‎Khu vựcSomalia, Djibouti, Vùng Somali, Tỉnh Đông Bắc (Kenya)Tổng số người nói15 triệu (2015)[1]Phân loạiPhi-ÁCushĐông Cush Đất thấpSomaliTiếng SomaliHệ chữ viếtBảng chữ cái Latinh (biến thể tiếng Somali)Chữ Ả Rập (Wadaad)Bảng chữ cái OsmanyaBảng chữ cái BoramaBảng chữ cái KaddareĐịa vị chính thứcNgôn ngữ chính thức tạiSomaliaNgôn...

Hyperboloïde de révolution à une nappe En mathématiques, la géométrie dans l'espace consiste à étudier les objets définis dans la géométrie plane dans un espace à trois dimensions et à y ajouter des objets qui ne sont pas contenus dans des plans : surfaces (plans et surfaces courbes) et volumes fermés. Il s'agit donc de géométrie dans un espace à trois dimensions. Géométrie euclidienne dans l'espace On peut adopter, dans l'espace à trois dimensions, les mêmes axiomes...

この項目では、専用貸切車両による有償旅客事業について説明しています。ひとつの乗り物に複数人数が一緒にのることについては「相乗り、乗合行為」をご覧ください。 ロシア、トムスクで稼働するUberの車両 ライドシェアリング（英語：Ridesharing）とは、ウェブサイトやモバイルアプリを介し、専用の貸切車両を運転する運転手と乗客をマッチングさせるサービス�...