Read other articles:

Voce principale: Cuoiopelli Cappiano Romaiano. Cuoiopelli Cappiano RomaianoStagione 2006-2007Sport calcio Squadra CuoioCappiano Allenatore Oliviero Di Stefano poi Agostino Iacobelli Presidente Michele Videtta e Carlo Battini Serie C210º posto nel girone B. Maggiori presenzeCampionato: Vettori (31) Miglior marcatoreCampionato: Banchelli (9) 2005-2006 2007-2008 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Cuoiopelli Cappiano Romaiano nelle c...

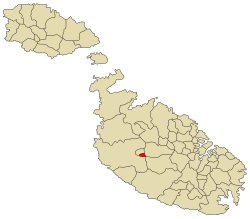
Artikel ini bukan mengenai Madinah. Mdina Il-Kunsill Lokali tal-ImdinaCittà NotabileThe Silent CityDewan lokalMdina BenderaLambang kebesaranMotto: Città NotabileNegara MaltaPulauMaltaBatasRabatPemerintahan • Wali kotaPeter Dei Conti Sant Manduca (Partai Nasionalis)Luas • Total0,9 km2 (0,3 sq mi)Populasi (Maret 2011) • Total306 • Kepadatan340/km2 (880/sq mi)DemonimMidjan (maskulin), Midjana (feminin), Midjani ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Raymond Robinson atau Green Man (29 Oktober 1910 – 11 Juni 1985) merupakan pria yang dikenal sebagai salah satu legenda urban di Pennsylvania. Ia mulai dikenal sejak kebiasaannya berjalan dimalam hari menarik perhatian warga setempat d...

Romantic landscape painter from England, 1802-1828 Richard Parkes BoningtonPortrait of Richard Parkes Bonington by Margaret Sarah CarpenterBorn(1802-10-25)25 October 1802Arnold, Nottinghamshire, EnglandDied23 September 1828(1828-09-23) (aged 25)London, EnglandNationalityBritish/FrenchEducationÉcole des Beaux-Arts, ParisMovementOrientalist, Romanticism Richard Parkes Bonington (25 October 1802[1] – 23 September 1828) was an English Romantic landscape painter, who moved to Franc...

Points utilisés pour une méthode de quadrature de Gauss. Dans le domaine mathématique de l'analyse numérique, les méthodes de quadrature sont des approximations de la valeur numérique d'une intégrale. En général, on remplace le calcul de l'intégrale par une somme pondérée prise en un certain nombre de points du domaine d'intégration (voir calcul numérique d'une intégrale pour plus d'informations). La méthode de quadrature de Gauss, du nom de Carl Friedrich Gauss[1], est une m�...

† Палеопропитеки Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:�...

South Korean actor This article is about the actor. For the singer, see Im Hyun-sik (singer). In this Korean name, the family name is Im. Im Hyun-sikBorn (1945-12-31) December 31, 1945 (age 78)Sunchang County, North Jeolla ProvinceEducationHanyang University - Theater and Film (1964) Kyung Hee University - Honorary Doctorate (2000)OccupationActorYears active1969-presentKorean nameHangul임현식Hanja林玄植Revised RomanizationIm Hyeon-sikMcCune–ReischauerIm Hyŏnsik Im Hyun-sik ...

坐标：43°11′38″N 71°34′21″W / 43.1938516°N 71.5723953°W / 43.1938516; -71.5723953 此條目需要补充更多来源。 (2017年5月21日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：新罕布什尔州 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源...

Combinatorial optimization problem Worked example of assigning tasks to an unequal number of workers using the Hungarian method The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform as many tasks as possible ...

Crocus Crocus longiflorus Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Monokotil Ordo: Asparagales Famili: Iridaceae Genus: CrocusL. Crocus adalah genus tanaman yang berasal dari wilayah besar dari pantai dan subalpin di Eropa Tengah dan Selatan (termasuk kepulauan di laut Aegea), Afrika Utara dan Timur Tengah, sampai Asia Tengah ke Tiongkok barat. Genus Crocus diletakkan di famili iris (Iridaceae). Crocus memiliki habitus ber...

Major alliance of World War II The Axis and Rome-Berlin Axis redirect here. For the book, see The Rome–Berlin Axis. For other uses, see Axis (disambiguation). Axis powersAchsenmächte (German)Potenze dell'Asse (Italian)樞軸國, Sūjikukoku (Japanese)1936–1945   Axis powers (occupied territory and their colonies)   Allies (and their colonies)   Allies entering after December 1941   Neutral countries and territories Major Axis powers:[a]  Ge...

نادي أبردين أف سي الشعار الاسم الكامل نادي أبردين إف سي اللقب السادة، الانيقون، الأغنام الاسم المختصر أبردين تأسس عام 14 أبريل 1903 (منذ 121 سنة) الملعب ملعب بيتودري(السعة: 20,897) البلد المملكة المتحدة  الدوري الدوري الاسكتلندي الممتاز 2019-20 الرابع الإدارة رئيس دايف كورماك المد...

This article is about the American blues pianist. For the American Chicago blues pianist and singer, see Piano C Red. American blues musician Piano RedBackground informationBirth nameWillie Lee PerrymanAlso known asDr. FeelgoodBorn(1911-10-19)October 19, 1911Near Hampton, Georgia, U.S.DiedJuly 25, 1985(1985-07-25) (aged 73)Decatur, Georgia, U.S.GenresBlues, R&BInstrument(s)Piano, vocalsYears active1930s–1980sMusical artist Willie Lee Perryman (October 19, 1911 – July 25, 1985),&#...

南瀛綠都心公園Nanying Green City Park基本資料類型城市公園位置 臺灣臺南市新營區民治路36號建造2006年1月25日營運者臺南市政府工務局公園管理科狀態全年開放停車場南瀛綠都心公園地下停車場總汽車位：285地圖 步道1 步道2 拱橋 太陽能屋頂 南瀛綠都心公園，是一座位於臺灣臺南市新營區的公園，緊鄰臺南市政府民治市政中心與臺南市議會民治議事廳，佔地約6.4公頃，由臺南�...

2017年世界羽毛球錦標賽蘇格蘭格拉斯哥   男單   女單   男雙   女雙   混雙 2017年世界羽毛球錦標賽為第23届世界羽毛球錦標賽，是一項全球性的羽毛球賽事。本條目為男子單打項目的比賽結果。 獎牌榜 項目獎牌榜 項目 金牌 银牌 铜牌 男子單打 维克托·阿萨尔森 林丹 孫完虎 谌龙 國家獎牌榜 排名 国家／地区 金牌 银牌 铜牌 總數 1 丹麦 1 0 0 1 2 中國 0 1 1 2 ...

Local government administrative areas in Western Australia Map of local government areas in Western Australia There are 137 local government areas (LGAs) in Western Australia,[1] which comprise 27 cities, 102 shires, and 8 towns that manage their own affairs to the extent permitted by the Local Government Act 1995.[2] The Local Government Act 1995 also makes provision for regional local governments (referred to as regional councils, established by two or more local governments...

В Википедии есть статьи о других людях с фамилией Глаубиц. Иоганн Кристоф Глаубиц Ворота базилианского монастыря (1761, Вильнюс) Основные сведения Страна Речь Посполитая Дата рождения 7 марта 1710(1710-03-07)[1] Место рождения Швайдниц, Силезия Дата смерти 30 марта 1767(1767...

English cricketer Thilan WalallawitaThilan Walallawita in 2022Personal informationFull nameThilan Nipuna WalallawitaBorn (1998-06-23) 23 June 1998 (age 26)Colombo, Sri LankaBattingLeft-handedBowlingSlow left-arm orthodoxRoleBowlerDomestic team information YearsTeam2020–presentMiddlesex (squad no. 32)2022/23Panadura Sports Club FC debut1 August 2020 Middlesex v SurreyLA debut25 July 2021 Middlesex v EssexCareer statistics Competition FC LA T20 Matches ...

This timeline of the history of the scientific method shows an overview of the development of the scientific method up to the present time. For a detailed account, see History of the scientific method. BC Nineteenth-century illustration of the ancient Great Library at Alexandria c.1600 BC – The Edwin Smith Papyrus, a unique ancient Egyptian text, contains practical and objective advice to physicians regarding the examination, diagnosis, treatment and prognosis, of injuries and ailments. ...

American actor For the Canadian football player, see Jim Conroy (Canadian football). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) The topic of this article may not meet Wikipedia's notability guideline for biographies. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere...