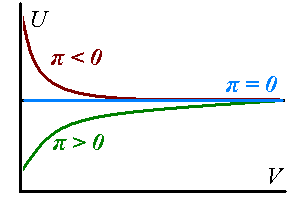
Internal pressure
|
Read other articles:

Andreas Hölzl Informasi pribadiTanggal lahir 16 Maret 1985 (umur 39)Tempat lahir Kitzbühel, AustriaTinggi 1,76 m (5 ft 9+1⁄2 in)Posisi bermain GelandangInformasi klubKlub saat ini SK Sturm GrazNomor 8Karier junior BNZ TirolKarier senior*Tahun Tim Tampil (Gol)2003-2008 FC Wacker Innsbruck 120 (12)2004 SV Wörgl (loan) 13 (1)2008-present SK Sturm Graz 95 (22)Tim nasional‡ Austria U-21 10 (0)2008-present Austria 9 (2) * Penampilan dan gol di klub senior hanya dihit...

Asha BhosleInformasi latar belakangNama lahirAsha MangeshkarLahir8 September 1933 (umur 90)Sangli, Bombay Presidency, India BritaniaGenremusik pop, musik rakyat, musik tradisional IndiaPekerjaanpenyanyi, penyanyi playbackTahun aktif1943–sekarang Asha Bhosle (bahasa Marathi: आशा भोंसले) (lahir 8 September 1933) adalah penyanyi wanita India yang dikenal sebagai penyanyi playback dalam film Bollywood. Karier sebagai penyanyi profesional dimulai sejak berusia 11 tahun...

Neighborhood of Cincinnati in Hamilton, Ohio, United StatesAvondaleNeighborhood of CincinnatiCarmel Presbyterian Church, Avondale FlagAvondale (red) within Cincinnati, OhioCountryUnited StatesStateOhioCountyHamiltonCityCincinnatiPopulation (2020) • Total11,345ZIP code45229 Rockdale Avenue, Avondale, March 2019 Avondale is one of the 52 neighborhoods of Cincinnati, Ohio. It is home to the Cincinnati Zoo and Botanical Garden. The population was 11,345 at the 2020 census.[1&...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

Football stadium in Bournemouth, England This article is about the football stadium in Bournemouth. For the community near Oxford, see Dean Court, Oxfordshire. Dean CourtPanorama of Dean Court from East StandFormer namesGoldsands StadiumSeward StadiumFitness First StadiumLocationKings ParkBournemouthDorsetBH7 7AFEnglandCoordinates50°44′07″N 1°50′18″W / 50.73528°N 1.83833°W / 50.73528; -1.83833OwnerStructadeneCapacity11,307[1]Record attendance28,799 ...

WarriorAlbum studio karya KeshaDirilis30 November 2012 (2012-11-30)DirekamJanuari–Agustus 2012Genre Electropop[1] rock[2] Durasi44:2758:43 (Edisi Deluxe)Label Kemosabe RCA Produser Ammo Benny Blanco Billboard Cirkut Dr. Luke Greg Kurstin Kool Kojak Matt Squire Max Martin Shellback Stardeath and White Dwarfs Steven Wolf The Flaming Lips Kronologi Kesha I Am the Dance Commander + I Command You to Dance: The Remix Album(2011) Warrior(2012) Deconstructed(2012) Singel da...

Entertainment Software Rating Board Logo de l’ESRB. Situation Région Canada États-Unis Mexique Création 16 septembre 1994 Siège New York, États-Unis Coordonnées 40° 45′ 10″ N, 73° 58′ 44″ O Langue Anglais, français, espagnol Site web www.esrb.org Géolocalisation sur la carte : New York Entertainment Software Rating Board Géolocalisation sur la carte : New York (État) Entertainment Software Rating Board Géolocalisation sur la cart...

American politician. Thomas J. Cunningham14th Secretary of State of WisconsinIn officeJanuary 5, 1891 – January 7, 1895GovernorGeorge Wilbur PeckPreceded byErnst TimmeSucceeded byHenry Casson15th and 28th Mayor of Chippewa Falls, WisconsinIn officeApril 1899 – April 1901Preceded byJ. A. AndersonSucceeded byL. A. FletcherIn officeApril 1885 – April 1886Preceded byJacob LeinenkugelSucceeded byHector McRaeMember of the Wisconsin State Assemblyfrom the Chi...

Type of tropical climate in which there is no dry season Worldwide zones of tropical rainforest climate (Af). A tropical rainforest climate or equatorial climate is a tropical climate sub-type usually found within 10 to 15 degrees latitude of the equator. There are some other areas at higher latitudes, such as the coast of southeast Florida, United States, and Okinawa, Japan that fall into the tropical rainforest climate category. They experience high mean annual temperatures, small temperatu...

Cek Endra Bupati Sarolangun ke-3Masa jabatan30 Juli 2011 – 22 Mei 2022 (Pelaksana Tugas: 9 Agustus 2010–30 Juli 2011)WakilPahrul RoziHilallatil BadriPendahuluHasan Basri AgusPenggantiHenrizal (Pj.)Wakil Bupati Sarolangun ke-2Masa jabatan30 Juli 2006 – 3 Agustus 2010BupatiHasan Basri AgusPendahuluMaryadi SyarifPenggantiPahrul Rozi Informasi pribadiLahir17 Maret 1958 (umur 66)Mandiangin, Sarolangun, JambiPartai politikPartai Amanat Nasional (sebelumnya)Parta...

Fictional character in the Arrowverse For the Arrow episode, see Spartan (Arrow episode). Fictional character John DiggleArrowverse and Superman & Lois characterDavid Ramsey as John Diggle in his Spartan suit as seen in the sixth season of ArrowFirst appearanceArrowverse version:PilotArrow Season 1×1October 10, 2012Superman & Lois version:Through the Valley of DeathSuperman & Lois Season 1×12July 14, 2021Last appearanceIt's My Party and I'll Die If I Want ToThe FlashApril 29, 20...

1970 single by Neil DiamondCracklin' RosieSingle by Neil Diamondfrom the album Tap Root Manuscript B-sideLordyReleasedJuly 30, 1970GenreSoft rock, popLength2:54LabelUniSongwriter(s)Neil DiamondProducer(s)Tom CatalanoNeil Diamond singles chronology Until It's Time For You To Go (1970) Cracklin' Rosie (1970) He Ain't Heavy, He's My Brother (1970) Cracklin' Rosie is a song written and recorded by Neil Diamond in 1970, with instrumental backing by Los Angeles session musicians from the Wrecking C...

Gubernatorial elections were held in Massachusetts November 14, 1836 1836 Massachusetts gubernatorial election ← 1835 November 14, 1836 (1836-11-14) 1837 → Nominee Edward Everett Marcus Morton Party Whig Democratic Alliance Anti-Masonic Popular vote 42,160 35,992 Percentage 53.78% 45.92% County ResultsEverett: 50-60% 60-70% 70-80%Morton: ...

Abadía imperial de QuedlinburgReichsstift Quedlinburg Abadía imperial 936-1802/1803 Escudo Castillo y abadía de QuedlinburgCoordenadas 51°47′09″N 11°08′13″E / 51.785944444444, 11.136805555556Capital QuedlinburgEntidad Abadía imperial • País Sacro Imperio GermánicoIdioma oficial Latín • Otros idiomas AlemánReligión CatolicismoPeríodo histórico Edades Media y Moderna • 936 Fundación • 1500 Círculo de Alta Sajonia • 1539 S...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. E-FunSoft Games Logo e-FunSoft Games Didirikan: April 2000 Jenis: Game Developer Lokasi: Yogyakarta, Indonesia e-FunSoft Games adalah game developer yang berasal dari Indonesia yang didirikan pada bulan April 2000 oleh Agung Wijaya di Yogyakarta. Pada...

Optimality criterion in which the shortest possible tree that explains the data is considered best This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Maximum parsimony phylogenetics – news · newspapers · books · scholar · JSTOR (July 2015) (Learn how and when to remove this message) This article may be too...

ستورم ليك الإحداثيات 42°38′37″N 95°12′07″W / 42.643611111111°N 95.201944444444°W / 42.643611111111; -95.201944444444 [1] تاريخ التأسيس 1873 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة بوينا فيستا عاصمة لـ مقاطعة بوينا فيستا خصائص جغرافية المس�...

U.S. Men's Clay Court Championships 1975Sport Tennis Data4 agosto – 10 agosto Edizione65ª CampioniSingolare Manuel Orantes Doppio Juan Gisbert / Manuel Orantes 1974 1976 L'U.S. Men's Clay Court Championships 1975 è stato un torneo di tennis giocato sulla terra. È stata la 65ª edizione del U.S. Men's Clay Court Championships, che fa parte del Commercial Union Assurance Grand Prix 1975. Si è giocato a Indianapolis negli Stati Uniti dal 4 al 10 agosto 1975. Indice 1 Campioni 1.1 Singolare...

Subset of a graph's vertices, including at least one endpoint of every edge Example graph that has a vertex cover comprising 2 vertices (bottom), but none with fewer. In graph theory, a vertex cover (sometimes node cover) of a graph is a set of vertices that includes at least one endpoint of every edge of the graph. In computer science, the problem of finding a minimum vertex cover is a classical optimization problem. It is NP-hard, so it cannot be solved by a polynomial-time algorithm if P �...

Musical ornamentation; splitting a note into shorter, faster notes For the rhythmic level dividing the pulse, see Metre (music) § Metric structure. Theme and some possible divisions In music, division (also called diminution or coloration)[clarification needed] refers to a type of ornamentation or variation common in 16th- and 17th-century music[1][irrelevant citation] in which each note of a melodic line is divided into several shorter, faster-moving notes, ofte...