Interactive proof system
|
Read other articles:

Aditi Rao HydariLahir28 Oktober 1986 (umur 37)Hyderabad, Andhra Pradesh (sekarang Telangana), IndiaAlmamaterUniversitas Lady Shri RamPekerjaanAktris PenyanyiPenariTahun aktif2004–sekarangSuami/istriSatyadeep Mishra, cerai tahun 2013Orang tuaEhsaan HydariVidya RaoKerabatKiran Rao (sepupu)Aditi Rao Hydari (lahir 28 Oktober 1986) adalah seorang aktris, penari, dan penyanyi berkebangsaan India yang bekerja di film Bollywood, Tamil, Malayalam, dan Telugu. Lihat juga Portal India Porta...

Katja KippingKatja Kipping pada 2014 Ketua Partai Partai KiriPetahanaMulai menjabat 2 June 2012Menjabat bersama Bernd Riexinger PendahuluGesine Lötzsch, Klaus ErnstPenggantiPetahanaAnggota Bundestag untuk Saxony Distrik I Dresden (list)PetahanaMulai menjabat 2005Anggota Parlemen SaxonyMasa jabatan1999–2004Anggota Dewan Kota DresdenMasa jabatan1999–2003 Informasi pribadiLahir18 Januari 1978 (umur 46)Dresden, Jerman TimurKewarganegaraanJermanPartai politikPartai Kiri (...

Dunia MimpiAlbum studio karya AriyoDirilis16 November 2002GenrepopLabelEMIProduserBongkyKronologi Ariyo -String Module Error: Match not foundString Module Error: Match not found Dunia Mimpi(2002) Live And Let Live(2002)Live And Let Live2002 Dunia Mimpi (digayakan sebagai Dunia>Mimpi) merupakan sebuah album musik perdana karya penyanyi dan aktor berkebangsaan Indonesia, Ariyo Wahab, yang dirilis tahun 2002. Lagu yang dijagokan dari album ini adalah “Kucinta Caramu” dan “Tiada yang...

Device for making an impression in wax or other medium For other uses, see Seal (disambiguation). Town seal (matrix) of Náchod (now in the Czech Republic) from 1570 Present-day impression of a Late Bronze Age seal A seal is a device for making an impression in wax, clay, paper, or some other medium, including an embossment on paper, and is also the impression thus made. The original purpose was to authenticate a document, or to prevent interference with a package or envelope by applying a se...

الدوري المقدوني الأول لكرة القدم 2017-18 تفاصيل الموسم الدوري المقدوني الأول لكرة القدم النسخة 26 البلد مقدونيا الشمالية التاريخ بداية:12 أغسطس 2017 نهاية:20 مايو 2018 المنظم اتحاد مقدونيا الشمالية لكرة القدم البطل نادي شكينديا الهابطون نادي بيليستر مبار...

Halaman ini berisi artikel tentang pengusaha. Untuk peneliti medikal, lihat Jawahar L. Mehta. Jay Mehta Informasi pribadiLahir18 Januari 1960 (umur 64)IndiaSuami/istriJuhi ChawlaAnak2[1]PekerjaanDirektur Grup operasi India (Mehta Group)Wakil Ketua Eksekutif (Saurashtra Cement Ltd dan Gujarat Sidhee Cement Ltd) Direktur Non-Eksekutif Independen dari ADF Foods LimitedSunting kotak info • L • B Jay Mehta adalah seorang pengusaha asal India. Ia adalah putra dari pasanga...
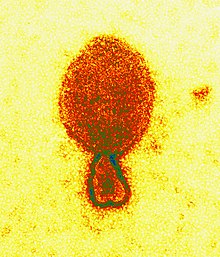
Virus Hendra Hendra virus Gambar mikrograf elektron berwarna dari virion Hendra henipavirus (memiliki panjang sekitar 300 nanometer)TaksonomiSuperdomainBiotaDomainVirusDuniaRiboviriaKerajaanOrthornaviraeFilumNegarnaviricotaSubfilumHaploviricotinaKelasMonjiviricetesOrdoMononegaviralesFamiliParamyxoviridaeSubfamiliParamyxovirinaeGenusHenipavirusSpesiesHendra virus lbs Virus Hendra, nama ilmiah Hendra henipavirus, merupakan virus yang dibawa oleh kelelawar yang menyebabkan infeksi mematikan pada...

Irish geographer Anne ButtimerBorn(1938-10-31)October 31, 1938Cork, IrelandDiedJuly 15, 2017(2017-07-15) (aged 78)Dublin, IrelandNationalityIrishAlma materUniversity College CorkUniversity of WashingtonScientific careerFieldsGeographyInstitutionsSeattle UniversityGrenoble Alpes UniversityUniversity of TexasLund UniversityClark University Anne Buttimer (31 October 1938 – 15 July 2017) was an Irish geographer. She was emeritus professor of geography at University College, Dublin. Ba...

Ode to the GoosePoster teatrikalNama lainHangul군산: 거위를 노래하다 Alih Aksara yang DisempurnakanGunsan: Geowileul Nolaehada SutradaraZhang LüProduserZhang LüDitulis olehZhang LüPemeranPark Hae-ilMoon So-riJung Jin-youngPark So-damSinematograferCho Young-jikPenyuntingZhang LüLee Hak-minPerusahaanproduksiLu FilmTanggal rilis 5 Oktober 2018 (2018-10-05) (BIFF) 8 November 2018 (2018-11-08) (Korea Selatan) Durasi122 menit[1]NegaraKorea SelatanBahasaK...

This article is about the New York high school. For the South Carolina high school, see Scholars Academy. 40°35′03″N 73°49′31″W / 40.5842°N 73.82535°W / 40.5842; -73.82535 SchoolThe Scholars' AcademyAddress320 Beach 104th St, Rockaway Park, NY 11694InformationEstablishedSeptember 2005PrincipalMichele SmythGrades6 to 12Color(s)Navy blue, light blue and khaki pantsSloganTechnology today, Smarter tomorrowTeam nameSeawolvesNewspaperThe Seaside ChronicleWebsiteh...

Football derby between Real Sociedad and Athletic Bilbao Not to be confused with Basque basketball derby. Basque derbyLocationBasque Country, SpainTeamsAthletic BilbaoReal SociedadFirst meeting4 April 1909Copa del ReyClub Ciclista 4–2 Athletic BilbaoLatest meeting13 January 2024La LigaAthletic Bilbao 2–1 Real SociedadStadiumsSan Mamés (Bilbao)Anoeta (San Sebastian)StatisticsMeetings total191Most winsAthletic Bilbao (79)Top scorerTelmo ZarraJesús María Satrústegui(14 each)Largest victo...

Indian cricketer (born 1993) In this Indian name, the name Ramaswamy Gopal is a patronymic, and the person should be referred to by the given name, Shreyas. Shreyas GopalGopal in a post-match presentation during 2019 IPLPersonal informationFull nameRamswamy Shreyas GopalBorn (1993-09-04) 4 September 1993 (age 30)Bangalore, Karnataka, IndiaBattingRight-handedBowlingRight-arm leg breakRoleAll-rounderDomestic team information YearsTeam2013/14–2022/23Karnataka2014–2017Mumbai Indians...

Ardizzone da CarraraSignore di Ascoli PicenoStemma TrattamentoSignore Altri titoliSignore di Civitella del Tronto ed Offida NascitaPadova MorteMontemerano, settembre 1441 DinastiaDa Carrara PadreConte da Carrara Madre? ConsorteAntonia Sforza Figlivedi sezione ReligioneCattolicesimo Ardizzone da CarraraNascitaPadova, ? MorteMontemerano, settembre 1441 Dati militariPaese servito Regno di Napoli Stato Pontificio Repubblica di Firenze Ducato di Milano Regno d'Aragona Repubblica...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

اتفاق انسحاب القوات الأمريكية من العراق جزء من حرب العراق التاريخ 18 ديسمبر 2011 الموقع العراق تعديل مصدري - تعديل اتفاق انسحاب القوات الأميركية من العراق هو الاتفاق الذي عقد بين القوات العراقية والأمريكية لجدولة انسحاب القوات الأمريكية من العراق وإخراج...

Trinamool Congress SingkatanAITCDibentuk1 Januari 1998; 26 tahun lalu (1998-01-01)Dipisah dariKongres Nasional IndiaBendera All India Trinamool Congress (AITC) atau Trinamool Congress (TMC) adalah sebuah partai politik di India yang terutamanya berbasis di Benggala Barat. Pemimpin partai adalah Mamata Banerjee yang telah menjadi Ketua Menteri Bengal Barat sejak tahun 2011. AITC merupakan partai terbesar ketiga setelah BJP dan INC dalam Parlemen India, dengan memiliki 23 anggota dala...

فسيفساء رومانية في جرش بالأردن للشاعرة اليونانية الكمان تظهر شرب الخمر. أواخر القرن الثاني والثالث معصرة نبيذ أثرية في عبدون يتم إنتاج النبيذ الأردني من قبل اثنين من مصانع النبيذ، مع إنتاج سنوي ما يقرب من مليون زجاجة في السنة. للأردن تقليد طويل في صناعة النبيذ، [1] يعود...

GR 7Lodève, sur le parcours du GR 7.LocalisationContinent EuropeLocalisation Espagne, Andorre et FranceDésignationAutre nom Du Ballon d'Alsace à Andorre-la-VieilleType Sentier de grande randonnée, sentier de longue randonnéeTracéPoint de départ Le Ballon d'Alsace Andorre-la-Vieille (Andorre)Extrémités Andorre-la-VieilleDétroit de GibraltarBallon d'AlsaceLongueur 1 471 kmmodifier - modifier le code - modifier Wikidata Le sentier de grande randonnée 7 (GR 7) suit appr...

Chemical solution in solid form This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Solid solution – news · newspapers · books · scholar · JSTOR (November 2007) (Learn how and when to remove this message) A solid solution, a term popularly used for metals, is a homogeneous mixture of two different kinds of atoms...

Australian physician (born 1960) Dale FisherBornDale Andrew Fisher1960 (age 63–64)Melbourne, AustraliaEducationCamberwell Grammar School, Melbourne, VictoriaHutchins School, Hobart, Tasmania,United World College of South East Asia, Singapore,University of Tasmania, Australia (MBBS)Medical careerFieldMedicine, Infectious DiseasesInstitutionsNational University HospitalNational University of Singapore Websitewww.nuh.com.sg/patients-visitors/Pages/find-a-doctor-details.aspx?docid=Dale...




![{\displaystyle \Pr[(\perp ,({\text{accept}}))\gets ({\tilde {\mathcal {P}}})(y)\leftrightarrow ({\mathcal {V}})(y)]<\epsilon .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89775f36bd79764d20bcbb10051edc1470cf8baa)









