Inductive type
|
Read other articles:

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أبريل 2020) منتخب تونس تحت 17 سنة لكرة السلة للسيدات تونس منتخب تونس تحت 17 سنة لكرة السلة للسيدات التصنيف 33 ▲ 18 (16 سب�...

Untuk Nabi yang sama dari sudut pandang Agama Yahudi & Kristen, lihat Ezra dan Simon Bar Kokhba. Situs yang diperkirakan merupakan makam Uzayr di Al-Uzayr dekat Basra. Uzayr (Arab: عزيرcode: ar is deprecated , 'Uzair, Turki: ' 'Üzeyir') adalah yang disebutkan dalam Al-Qur'an surah At-Taubah ayat 30 yang dipercaya oleh orang Yahudi sebagai Putra Allah.[1] Meskipun Al-Qur'an tidak menyatakan Uzair sebagai nabi, ia dianggap sebagai nabi oleh sebagian ulama yang berdasarkan t...

Delimited medium where some stimuli can evoke neuronal responses Not to be confused with Reflexogenous zone. The receptive field, or sensory space, is a delimited medium where some physiological stimuli can evoke a sensory neuronal response in specific organisms.[1] Complexity of the receptive field ranges from the unidimensional chemical structure of odorants to the multidimensional spacetime of human visual field, through the bidimensional skin surface, being a receptive field for t...

Indian Muslim scholar and politician MawlanaSyed Ahmad HashmiMP, Rajya Sabha for Uttar PradeshIn office3 April 1974 – 2 April 1980In office5 July 1980 – 4 July 19867th General Secretary of Jamiat Ulama-e-HindIn office11 August 1973 – 28 January 1980Preceded byAsad MadniSucceeded byAsrarul Haq Qasmi PersonalBorn(1932-01-17)17 January 1932Darbhanga, Bihar and Orissa Province, British IndiaDied4 November 2001(2001-11-04) (aged 69)Delhi, IndiaReligionIslamNat...
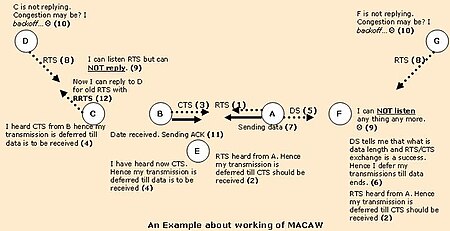
Slotted medium access control protocol widely used in ad hoc networks Multiple Access with Collision Avoidance for Wireless (MACAW)[1] is a slotted medium access control (MAC) protocol widely used in ad hoc networks.[2] Furthermore, it is the foundation of many other MAC protocols used in wireless sensor networks (WSN).[2] The IEEE 802.11 RTS/CTS mechanism is adopted from this protocol.[3][4] It uses RTS-CTS-DS-DATA-ACK frame sequence for transferring d...

American baseball player (born 1991) Baseball player Alex WoodWood with the Los Angeles Dodgers in 2018Oakland Athletics – No. 57PitcherBorn: (1991-01-12) January 12, 1991 (age 33)Charlotte, North Carolina, U.S.Bats: RightThrows: LeftMLB debutMay 30, 2013, for the Atlanta BravesMLB statistics (through April 14, 2024)Win–loss record76–66Earned run average3.80Strikeouts1,156 Teams Atlanta Braves (2013–2015) Los Angeles Dodgers (2015–2018) Cincinnati Reds (2019) Los...

Jordi Osei-Tutu Nazionalità Inghilterra Altezza 176 cm Peso 70 kg Calcio Ruolo Centrocampista Squadra PAS Giannina Carriera Giovanili 20??-2015 Reading2015-2019 Arsenal Squadre di club1 2019-2020→ Bochum21 (5)2020-2021→ Cardiff City8 (0)2021-2022→ Nottingham Forest4 (0)2022→ Rotherham Utd14 (0)2022-2024 Bochum20 (0)2024-→ PAS Giannina0 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campiona...

Carlo Albini Nazionalità Italia Italia (dal 1946) Calcio Ruolo Difensore Termine carriera 1949 Carriera Squadre di club1 1935-1949 Brescia327 (20) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Carlo Albini (Brescia, 22 marzo 1914 – Rho, 18 novembre 1976) è stato un calciatore italiano, di ruolo terzino. Indice 1 Carriera 2 Statis...

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...

Fort Orange redirects here. For other uses, see Fort Orange (disambiguation). United States historic placeFort Orange Archeological SiteU.S. National Register of Historic PlacesU.S. National Historic Landmark Fort Orange in c1630 (Rensselaerswyck map detail)Show map of New YorkShow map of the United StatesLocationAlbany, New YorkCoordinates42°38′41.46″N 73°45′1.05″W / 42.6448500°N 73.7502917°W / 42.6448500; -73.7502917Built1624NRHP reference No.93...

Steam locomotive of the North British Railway NBR Class N LNER Class D25Cowlairs Works, North British Railway (NBR) No. 592Type and originPower typeSteamDesignerMatthew HolmesBuilderNorth British Railway (Cowlairs)Build date1886-1888Rebuilt 1911Total produced12SpecificationsConfiguration: • Whyte4-4-0Gauge4 ft 8+1⁄2 in (1,435 mm)Leading dia.3 ft 6 in (1.07 m)Coupled dia.7 ft 0 in (2.13 m)Length22 ft 4 in (6....

Giancarlo GiorgettiGiancarlo Giorgetti nel 2022 Ministro dell'economia e delle finanzeIn caricaInizio mandato22 ottobre 2022 Capo del governoGiorgia Meloni PredecessoreDaniele Franco Ministro dello sviluppo economicoDurata mandato13 febbraio 2021 –22 ottobre 2022 Capo del governoMario Draghi PredecessoreStefano Patuanelli SuccessoreAdolfo Urso[1] Vicesegretario federale della Lega per Salvini PremierIn caricaInizio mandato31 gennaio 2020 Vice diMatteo Salvini...

English merchant who assassinated Prime Minister Spencer Perceval in 1812 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: John Bellingham – news · newspapers · books · scholar · JSTOR (September 2019) (Learn how and when to remove this message) This article includes a list of references, related reading, or ...

Inez Elodhia MaharaniInez saat tampil pada Miss Earth 2011LahirInez Elodhia Maharani16 Juni 1989 (umur 34) Jakarta, IndonesiaPekerjaanArsitekperancang interiorpenyanyiTahun aktif2002–sekarangSuami/istriDony Safitra (m. 2021) Inez Elodhia Maharani (lahir 16 Juni 1989) adalah peserta kontes kecantikan dan model Indonesia. Ia berkompetisi pada kontes Miss Indonesia Earth 2010 dan meraih gelar Miss Earth Indonesia – Water,[1] serta mewakili In...

Danish film director and script writer Ole Christian Madsen. Ole Christian Madsen (born 18 June 1966) is a Danish film director and script writer. Among his most successful projects are the movies Flame & Citron, Prag, Angels in Fast Motion (da. Nordkraft) and the TV series Rejseholdet and Edderkoppen (The Spider). Madsen was a part of the Golden Year graduating from the Danish Film school as he graduated alongside Thomas Vinterberg and Per Fly. Madsen started his film career by directing...

Wines made from grapes grown in Arkansas ArkansasWine regionOfficial nameState of ArkansasTypeU.S. stateYear established1836CountryUnited StatesSub-regionsAltus AVA, Arkansas Mountain AVA, Ozark Mountain AVA[1]Climate regionHumid subtropical/continental in highlandsTotal area53,179 square miles (137,733 km2)Grapes producedCabernet Sauvignon, Catawba, Chardonnay, Concord, Edelweiss, Merlot, Müller-Thurgau, Muscadine, Niagara, Norton, Scheurebe, Seyval blanc, Verdelet, Vidal blanc...

Declaration of WarPoster filmSutradaraValérie DonzelliProduserEdouard WeilDitulis olehJérémie ElkaïmValérie DonzelliPemeranValérie DonzelliSinematograferSébastien BuchmannPenyuntingPauline GaillardDistributorWild Bunch DistributionTanggal rilis 12 Mei 2011 (2011-05-12) (Cannes) Durasi100 menitNegaraPrancisBahasaPrancisAnggaran€1.5 jutaPendapatankotor$6.5 juta[1] Declaration of War (bahasa Prancis: La Guerre est déclarée) adalah sebuah film Prancis tahun 2011 ya...

Residential institution devoted to the care of orphans This article is about the institution. For other uses, see Orphanage (disambiguation). The article's lead section may need to be rewritten. Please help improve the lead and read the lead layout guide. (August 2022) (Learn how and when to remove this message) Plaque where once stood the ruota (the wheel), the place to abandon children at the side of the Chiesa della Pietà, the church of an orphanage in Venice. The plaque cites on a Papal ...

Manuel Velázquez de León y Pérez Miembro de la Regencia del Imperio Mexicano 28 de septiembre de 1821-11 de abril de 1822Predecesor Junta Provisional GubernativaSucesor Regencia (Segundo Consejo) Información personalNacimiento Siglo XVIII Fallecimiento Siglo XIX Nacionalidad MexicanaInformación profesionalOcupación Político Lealtad Primer Imperio Mexicano Conflictos Independencia de México [editar datos en Wikidata] Manuel Velázquez de León y Pérez fue un político mexica...

艾哈邁德·蒂揚個人資料全名Ahmed Tijan Janko国家或地区卡達出生 (1995-04-28) 1995年4月28日(29歲)甘比亞班竹身高1.85公尺體重75公斤沙灘排球資料前任隊友 隊友 舍里夫·尤諾斯 榮譽 男子沙灘排球 代表 卡塔尔 夏季奧運 2020 東京 團體 亞洲運動會 2018 雅加達-巨港 男子 艾哈邁德·蒂揚·揚科(阿拉伯语:أحمد تيجان,1995年4月28日—)是甘比亞裔卡達籍沙灘排球運動員&#...











