House monotonicity
| |||||||||||||||||||||||||||||||
Read other articles:

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Jerry (Jerome a mouse)Tokoh Tom & JerryyDesain Jerry dalam film pendek Hanna-Barbera.PenampilanperdanaPuss Gets the Boot (sebagai Jinx)Midnight Snack (sebagai Jerry)PenciptaWilliam HannaJoseph BarberaPengisi suaraLihat di siniInformasiSpesiesTikus rumahJenis kelaminJantanKeluargaNibble/Nibbles (bangsal/keponakan)KerabatPaman Pecos (paman)Muscles (sepupu)Dinky (keponakan)Ibu yang tidak disebutkan namanya Jerry Mouse adalah karakter fiksi dan salah satu dari dua protagonis utama tituler (ya...

This article reads like a press release or a news article and may be largely based on routine coverage. Please help improve this article and add independent sources. (December 2015) Neven MaguireBorn (1973-12-01) 1 December 1973 (age 50)Blacklion, County Cavan, IrelandEducationEnniskillen Campus CAFRE[1]Culinary career Current restaurant(s) McNeans Bistro, Blacklion, County Cavan Television show(s) 10 of the Best Neven Cooks Cooking with Love Neven's Food from the Sun Websitehttp...

River in North Carolina, United States For the town of Haw River, North Carolina, see Haw River, North Carolina. For the North Carolina wine region, see Haw River Valley AVA. Haw RiverTributary to Cape Fear RiverConvergence of the Haw River and Great Alamance Creek in Swepsonville, NCMap of the Cape Fear drainage basin showing Haw RiverEtymologyEastern Sioux for piedmont or foothillNative namesak'yápha: (Catawba)LocationCountryUnited StatesStateNorth CarolinaRegionForsyth County, North ...

American game programmer Corrinne YuCorrinne Yu at Hotel W Dallas in 2009BornHong KongNationalityAmericanOccupationGame programmerEmployerGeneral MotorsTitleGraphics ProgrammerSpouseKenneth Scott Corrinne Yu is an American game programmer. She has worked on games including King's Quest, Quake II, and Halo 4. Her engine work included Unreal Engine 3, Microsoft's Direct3D Advisory Board, and CUDA and GPU simulation at Nvidia. She has also designed accelerator experiments for nuclear physics res...

Pour les articles homonymes, voir De Sève. Jacques de SèveBiographieNaissance 1715ParisDécès 1795ParisNationalité françaiseActivité Peintre, dessinateur pour l’Histoire naturelle de BuffonPériode d'activité 1742-1788Enfant Jacques Eustache de Sève (d)modifier - modifier le code - modifier Wikidata Le Lynx. Illustration de Jacques de Sève pour l’Histoire des Quadrupèdes de Buffon. Jacques de Sève (Paris, 1715 - Paris, 1795[1]) est un dessinateur, graveur et illustrateur fran�...

Overview of the events of 2023 in sports Years in sports ← 2020 2021 2022 2023 2024 2025 2026 → 2023 in sports Air sports American football Aquatic sports Association football Athletics Badminton Baseball Basketball Canadian football Chess Climbing Combat sports Sumo Cricket 2022–23 2023 2023–24 Cycling Dance sports Darts Equestrianism Esports Field hockey Flying disc Golf Gymnastics Handball Ice hockey Ice sports Korfball Lumberjack sports Mind sports Modern pentathlon Motorsport Or...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Republik Puntland adalah sebuah sebuah negara pengakuan terbatas di bagian timur laut Somalia yang tidak diakui oleh siapapun. Nama Puntland diambil dari Negeri Punt, kini mencakupi wilayah Somalia, yang berasal dari narasumber pada zaman Mesir kuno. Republik PuntlandJamhuuriyadda Putland Bendera Lambang Semboyan: Nabad iyo nolol(Indonesia: Kedamaian dan kehidupan)Lagu kebangsaan: Qolobaa Calankeed (Indonesia: Memuji Tanah Air) Ibu kotaGarooweBahasa resmiSomali, Arab, InggrisAgama ...
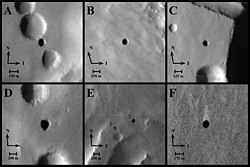
This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. This is a list of caves of the world that have articles or that are properly cited. They are sorted by continent and then country. Caves which are in overseas territories on a different continent than the home country are sorted by the territory's continent and name. Africa The Cango caves in western cape. African cave paintings Lithic Ind...

Budaya tradisional Korea diwarisi oleh rakyat Korea Utara dan Korea Selatan,[1] walaupun keadaan politik yang berbeda telah menghasilkan banyak perbedaan dalam kebudayaan modern Korea. Arsitektur istana Deoksugung Perayaan lentera Kehidupan Hanok, rumah tradisional Korea Hanok tipe chogajip (rumah beratap jerami) di Desa Rakyat Korea, Seoul Artikel utama: Arsitektur Korea dan Hanok Rumah Masyarakat tradisional Korea memilih tempat tinggal berdasarkan geomansi. Orang Korea meyakini bah...

American lawyer and academic For other people with the surname Goldsmith, see Goldsmith (surname). Jack GoldsmithGoldsmith in 2019United States Assistant Attorney General for the Office of Legal CounselIn officeOctober 2003 – July 2004PresidentGeorge W. BushPreceded byJay S. BybeeSucceeded byDaniel Levin (acting) Personal detailsBornJack Landman Goldsmith III (1962-09-26) September 26, 1962 (age 61)Memphis, Tennessee, U.S.[1]EducationWashington and Lee University (BA)U...

Map of (Roman-rite) Catholic Dioceses in China (PRC) as of February 2024 The Catholic Church in China comprises 152 Latin jurisdictions: 21 ecclesiastical provinces (including one for Taiwan), consisting of 21 metropolitan archdioceses and 100 suffragan dioceses 29 apostolic prefectures 1 exempt diocese, the Diocese of Macau 1 apostolic administration, the Apostolic Administration of Harbin Furthermore, the Eastern Catholic (Byzantine rite) Russian Greek Catholic Church has an exempt apostol...

Polish state space agency Not to be confused with Pölsa or Polsat. Polish Space AgencyPolska Agencja Kosmiczna (Polish)LogoAgency overviewAbbreviationPOLSAFormed26 September 2014; 9 years ago (2014-09-26)TypeSpace agencyHeadquartersGdańsk, PolandOfficial languagePolishAdministratorGrzegorz WrochnaOwnerPolandAnnual budget42.7 million PLN (2021)[1]Websitepolsa.gov.pl The Polish Space Agency (POLSA; Polish: Polska Agencja Kosmiczna, PAK) is the space agency of Poland,...

Baling-baling angin ini menunjukkan angin timur. Arah angin dilaporkan oleh arah asalnya. Misalnya, angin dari utara bertiup dari utara ke selatan.[1] Arah angin biasanya dilaporkan dalam arah mata angin atau dalam derajat azimut. Arah angin diukur dalam derajat searah jarum jam dari arah utara. Akibatnya, angin yang bertiup dari utara memiliki arah angin 0° (360°); angin yang bertiup dari timur memiliki arah angin 90°; angin bertiup dari selatan memiliki arah angin 180°; dan angi...

رابطة الجامعات البحثية الأوروبية رابطة الجامعات البحثية الأوروبية البلد بلجيكا المقر الرئيسي لُوفِن تاريخ التأسيس 2002 عدد الأعضاء 24 (فبراير 2024)[1] الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل رابطة الجامعات البحثية الأوروبية (بالإنجليزية: L...

المغرب منتخب المغرب لكرة الماء اللقب أسود الأطلس الإتحاد القاري CANA (أفريقيا) FINA code MAR الدوري العالمي الظهور 1 (أول مرة في 2008) أفضل نتيجة الدور التمهيدي 2008 تعديل مصدري - تعديل منتخب المغرب لكرة الماء هو الفريق الذي يمثل المغرب في منافسات كرة الماء للرجال. النتائج الدوري ال�...
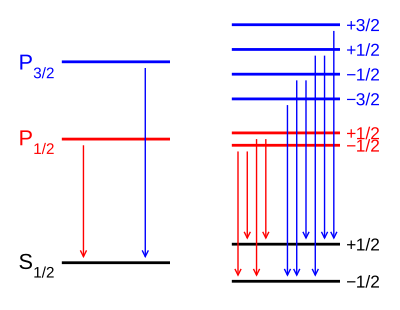
تأثير زيمان[1] هو ظاهرة انشقاق خطوط الطيف لمصدر تحت تأثير مجال مغناطيسي ثابت إلى عدة خطوط؛ أي أن تأثير زيمان يشق خطوط الطيف إلى خطوط متوازية عندما يوضع مصدر الضوء في مجال مغناطيسي شديد .[2][3][4] وهو تاثير يرجع إلى العالم الهولندي بيتر زيمان الذي اكتشف هذه الظاه...

Frank SpotnitzSpotnitz pada 2015Lahir17 November 1960 (umur 63)Kamp Zama, JepangAlmamaterAmerican Film InstitutePekerjaanProduser eksekutif, pemandu acara, penulis Frank Spotnitz (lahir 17 November 1960) adalah seorang produser dan penulis televisi Amerika Serikat Filmografi The X-Files (1996–2002) Inside the X-Files (1998) Harsh Realm (1999–2000) The Lone Gunmen (2001) Robbery Homicide Division (2002–2003) Night Stalker (2005–2006) A.M.P.E.D. (2007) The X-Files: I Want to Belie...

Tagore Abu Bakar (lahir 20 April 1954) adalah seorang politikus Indonesia kelahiran Takengon, Aceh. Tagore memulai karir politiknya setelah meraih gelar sarjana di Universitas Sumatera Utara pada tahun 1983. Tagore terjun ke dunia politik bersama Golkar. Ia tercatat telah menjadi petinggi partai Golkar dengan menjabat sebagai ketua DPD II Golkar Aceh Tengah periode 1998-2003. Setelah itu, Tagore melanjutkan karir politiknya sebagai ketua DPD II Golkar di Kabupaten Bener Meriah periode 2003-20...







