Holiday for Henrietta

Holiday for Henrietta
Directed byJulien Duvivier
Written byJulien Duvivier
Henri Jeanson
Produced byJosé Bosch
Georges Lourau
Arys Nissotti
Pierre O'Connell
StarringDany Robin
Michel Auclair
Hildegard Knef
CinematographyRoger Hubert
Edited byMarthe Poncin
Music byGeorges Auric
Production
companies
Filmsonor
Regina Films
Distributed byCinédis
Release date
  • 17 December 1952 (1952-12-17)
Running time
118 minutes
CountryFrance
LanguageFrench

Holiday for Henrietta (French: La fête à Henriette) is a 1952 French comedy film directed by Julien Duvivier and starring Dany Robin, Michel Auclair, and Hildegard Knef.[1] It was shot at the Billancourt Studios and on location around Paris including at the Gaumont-Palace cinema. The film's sets were designed by the art director Jean d'Eaubonne. Holiday for Henrietta was remade in English as the 1964 film Paris When It Sizzles, starring William Holden and Audrey Hepburn,[2] which also featured d'Eaubonne as art director.

Synopsis

While urgently trying to develop a screenplay for a new film, two screenwriters, the downbeat Crémieux and the optimist Seignier, create contradictory storylines as they argue, and as each takes turns in taking the narrative forward, they force the lead characters Henriette and Maurice into weird situations. The film switches back and forth between the writers at home and the film as it develops according to their ideas.

Cast

References

  1. ^ BFI.org
  2. ^ Crisp p.243

Bibliography

  • Crisp, Colin. French Cinema—A Critical Filmography: Volume 2, 1940–1958. Indiana University Press, 2015.


Stub icon

This article related to a French film of the 1950s is a stub. You can help Wikipedia by expanding it.

Stub icon

This film article about a 1950s comedy film is a stub. You can help Wikipedia by expanding it.

Read other articles:

Vinci Malizon

Nama ini menggunakan kebiasaan penamaan Filipina; nama tengah atau nama keluarga pihak ibunya adalah Malizon. VinciMalizon pada tahun 2023LahirGabriel Vincent Tolentino Malizon11 Maret 2000 (umur 23)Santo Tomas, Batangas, FilipinaKebangsaanFilipinaTahun aktif2022–sekarangKarier musikGenrePopInstrumen Vokal Tahun aktif2022–sekarangLabelMLDABS-CBNNama KoreaHangul빈치 Alih AksaraBin ChiMcCune–ReischauerPin Ch'i Tanda tangan Gabriel Vincent Tolentino Malizon (lahir 11 Maret 2000...

 

 

Midpoint method

Numeric solution for differential equations For the midpoint rule in numerical quadrature, see rectangle method. Illustration of the midpoint method assuming that y n {\displaystyle y_{n}} equals the exact value y ( t n ) . {\displaystyle y(t_{n}).} The midpoint method computes y n + 1 {\displaystyle y_{n+1}} so that the red chord is approximately parallel to the tangent line at the midpoint (the green line). In numerical analysis, a branch of applied mathematics, the midpoint method is a one...

 

 

Reichstag (Sacro Romano Impero)

Questa voce o sezione sugli argomenti parlamenti e Germania non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Il Reichstag (/ˈʀaɪ̯xsˌta:k/) o Dieta imperiale fu il massimo organo legislativo del Sacro Romano Impero. La sua evoluzione nei secoli portò questa sorta di parlamento di príncipi ad essere c...

Mount San Jacinto State Park

Place in California listed on National Register of Historic Places Mount San Jacinto State ParkIUCN category Ib (wilderness area)[1]Rock formation and trees seen from Round Valley trail in winterShow map of CaliforniaShow map of the United StatesLocationRiverside County, California, United StatesNearest cityIdyllwild, CaliforniaCoordinates33°48′N 116°40′W / 33.800°N 116.667°W / 33.800; -116.667Area14,000 acres (5,700 ha)Established1933Governin...

 

 

Stadio Aldo Campo

Questa voce o sezione sugli argomenti stadi di rugby e stadi di calcio d'Italia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Stadio Aldo CampoStadio Selvaggio Informazioni generaliStato Italia UbicazioneVia Avvocato Giovanni Alberto Cartia, Contrada Selvaggio,97100 Ragusa (RG) Inizio lavori1960 Inaugurazione1968 Proprietario Comune di Ragusa Info...

 

 

Oasi

Disambiguazione – Se stai cercando altri significati, vedi Oasi (disambigua). Un'oasi in Oman In geografia, un'oasi è un'area di vegetazione isolata in un deserto, che di solito circonda una sorgente o una simile fonte d'acqua naturale. Indice 1 Origine e uso del termine 2 Storia 3 Natura delle oasi 4 Oasi e società 5 Esempi di oasi 6 Note 7 Bibliografia 8 Altri progetti 9 Collegamenti esterni Origine e uso del termine La parola oasi deriva dal greco (oasis), che deriva a sua volta dall'...

Limpet

Group of snails This article is about the snails. For the wave power device, see Islay LIMPET. For the underwater explosive device, see Limpet mine. The true limpet species Patella vulgata on a rock surface in Wales Underside of a Patella vulgata specimen Limpets are a group of aquatic snails with a conical shell shape (patelliform) and a strong, muscular foot. This general category of conical shell is known as patelliform (dish-shaped).[1] Existing within the class Gastropoda, limpet...

 

 

Mandala (political model)

Southeast Asian pseudo-feudalistic political model between 5th and 15th century For other uses, see Mandala (disambiguation). Notable mandalas in classical Southeast Asian history (c. 5th to 15th century). From north to south; Bagan, Ayutthaya, Champa, Angkor, Srivijaya and Majapahit. Part of a series onPolitical andlegal anthropology Basic concepts Status and rank Ascribed status Achieved status Social status Caste Age grade/Age set Leveling mechanism Leadership Big man Patriarchy Matriarchy...

 

 

Novaya Zemlya

Novaya Zemlya Novaya Zemlya (bahasa Rusia: Но́вая Земля́, juga dieja Novaja Zemlja, lit. Tanah Baru; juga dikenal dalam bahasa Inggris dan Belanda sebagai Nova Zembla, Norwegia Gåselandet (Tanah Angsa)) adalah sebuah kepulauan di Samudra Arktik di utara Rusia dan titik ekstrem timur laut di Eropa di Tanjung Zhelaniya (lihat juga titik ekstrem di Eropa). Kepulauan ini dikelola oleh Oblast Arkhangelsk sebagai Wilayah Pulau Novaya Zemlya. Populasinya sekitar 2.716 jiwa (sensus 2...

Sponge

Animals of the phylum Porifera This article is about the phylum of aquatic animal. For the porous cleaning tool, see Sponge (tool). For other uses, see Sponge (disambiguation). SpongesTemporal range: Ediacaran-present; probable Cryogenian record,[1] 650–0 Ma Pha. Proterozoic Archean Had. A stove-pipe sponge Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: PoriferaGrant, 1836 Classes Calcarea Demospongiae Hexactinellida Homoscleromorpha †Archaeocyatha †H...

 

 

Kostroma

Kostroma kota Кострома (ru) flag of Kostroma (en) coat of arms of Kostroma (en) Tempat Negara berdaulatRusiaOblast di RusiaOblast KostromaUrban okrug in Russia (en) Kostroma Urban Okrug (en) Ibu kota dariKostromskoy District (en) Kostroma Urban Okrug (en) NegaraRusia PendudukTotal269.711  (2008 )GeografiLuas wilayah144,5 km² [convert: unit tak dikenal]Ketinggian110 m SejarahPembuatan1152 Organisasi politik• Kepala pemerintahanYuri Zhurin (en)  (2011 )Informa...

 

 

AMP-69

AMP-69 Jenis Senapan serbu Negara asal  Hungaria Sejarah pemakaian Masa penggunaan 1970-1985 Digunakan oleh Hungaria Sejarah produksi Perancang Károly Zala[1] Tahun Awal 1970an Spesifikasi Panjang 920mm (popor dibuka)640 mm (popor dilipat) Peluru 7,62 x 39 mmGranat 40 mm Mekanisme Operasi gas Kecepatan peluru 715 m/s Jarak efektif 350 m Amunisi Magazen box 30 butir,Magazen isi 5 butir (Mode pelontar granat) Alat bidik Bidikan optik AMP–69 (AMP da...

Alan Scholefield

Alan Scholefield Alan Scholefield (Città del Capo, 15 gennaio 1931 – 26 ottobre 2017) è stato uno scrittore sudafricano famoso per la sua serie Macrae & Silver. È famoso inoltre per aver scritto il romanzo Dirty Weekend del 1990 e per la serie Winter's Crimes. Indice 1 Opere 1.1 Serie 1.1.1 Macrae and Silver 1.1.2 Dr. Anne Vernon 1.2 Altri romanzi 1.3 Antologie pubblicate 2 Note 3 Bibliografia 4 Collegamenti esterni Opere Serie Macrae and Silver Dirty Weekend (1989) Never Die in Janu...

 

 

Slave trade in the Mongol Empire

Part of a series onForced labour and slavery Contemporary Child Labour Child soldiers Conscription Debt Forced marriage Bride buying Child marriage Wife selling Forced prostitution Human trafficking Peonage Penal labour Contemporary Africa 21st-century jihadism Sexual slavery Wage slavery Historical Antiquity Egypt Babylonia Greece Rome Medieval Europe Ancillae Black Sea slave trade Byzantine Empire Kholop Prague slave trade Serfs History In Russia Emancipation Thrall Genoese slave trade Ven...

 

 

Nokia C3-00

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Nokia C3-00 – berita · surat kabar · buku · cendekiawan · JSTOR Nokia C3-00PembuatNokiaSeriNokia Seri CFaktor bentukCandybarDimensi115.5 x 58.1 x 13.6 mmBerat87.7 g (dengan battery)Sistem OperasiSeries 4...

Djibril Cissé

Djibril Cissé Cissé Jugando en 2008Datos personalesNacimiento Arlés, Francia12 de agosto de 1981 (43 años)Nacionalidad(es)  FrancesaMarfileña MarfileñaAltura 1,83 metrosCarrera deportivaDeporte FútbolClub profesionalDebut deportivo 1998(AJ Auxerre)Posición DelanteroGoles en clubes 238 (567 PJ)Retirada deportiva 2021(Panathinaikos Chicago)Selección nacionalSelección FRA FranciaDebut 18 de mayo de 2002Dorsal(es) 7Part. (goles) 41 (9)[ Página web oficial]...

 

 

Allegory of the cave

Allegory by Plato Plato's allegory of the cave by Jan Saenredam, according to Cornelis van Haarlem, 1604, Albertina, Vienna Part of a series onPlatonism Life Works Theory of forms Form of the Good Theory of soul Epistemology Political philosophy Euthyphro dilemma Demiurge Atlantis The Republic Allegory of the cave Analogy of the Sun Analogy of the divided line Philosopher king Ship of State Ring of Gyges Myth of Er The works of Plato Euthyphro Apology Crito Phaedo Cratylus Theaetetus Sophist ...

 

 

キリンホールディングス

この項目では、2007年7月1日以降のキリンホールディングスについて説明しています。2007年6月30日以前のキリンホールディングスについては「麒麟麦酒」をご覧ください。 キリンホールディングス株式会社Kirin Holdings Company, Limited 本社のある中野セントラルパークサウス種類 株式会社機関設計 監査役会設置会社[1]市場情報 東証プライム 25031949年5月16日上場 名証プ...

Benjamin Auer

Benjamin AuerNazionalità Germania Altezza186 cm Calcio RuoloAttaccante Termine carriera2015 CarrieraGiovanili /1988HSV Landau1988-1996FSV Offenbach1996-1999 Kaiserslautern Squadre di club1 1999-2000 Karlsruhe14 (1)2000-2002 Borussia M'gladbach25 (3)2002-2006 Magonza116 (30)2006-2007 Bochum2 (0)2007-2008→ Kaiserslautern7 (0)2008-2012 Alemannia Aquisgrana125 (56)2015 Pirmasens12 (4) Nazionale 2002-2004 Germania U-2123 (15) 1 I due numeri indicano ...

 

 

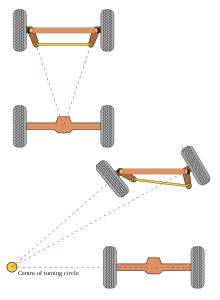
Sterzo

Disambiguazione – Se stai cercando la pratica selvicolturale, vedi Taglio a sterzo. Questa voce o sezione sull'argomento automobili non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Sistema di sterzo di un'auto, che sfrutta appieno l'angolo di Ackermann L'impianto sterzante o sterzo è l'insieme di el...