Gerhard Gentzen
| |||||||||||||||||||||||
Read other articles:

Partai Revolusi Chama Cha Mapinduzicode: sw is deprecated (Swahili)SingkatanCCMKetua umumSamia SuluhuSekretaris JenderalDaniel ChongoloJuru bicaraSophia MjemaWakil KetuaAbdurahman Omar KinanaPendiriJulius NyerereAboud JumbeDibentuk5 Februari 1977 (1977-02-05)Lambang pemiluCangkul dan paluBendera Chama Cha Mapinduzi (CCM; Swahili: terj. har. 'Partai Revolusi') adalah sebuah partai pemerintahan dominan di Tanzania dan partai pemerintahan terlama kedua di Afrika, hanya...

Dahshur - Piramida Merah - Polisi turis di atas unta Dahshur[transliteration 1] (dalam bahasa Inggris sering disebut Dashur; bahasa Arab: دهشور Dahšūr pelafalan [dɑhˈʃuːɾ], bahasa Koptik: ⲧⲁϩϭⲟⲩⲣ Dahchur[1]) merupakan sebuah nekropolis kerajaan yang terletak di gurun bagian barat sungai Nil sekitar 40 kilometer (25 mi) selatan Kairo. Wilayah ini dikenal memiliki beberapa piramida, dua di antaranya adalah yang tertua, terbesar ...

The Love Gov beralih ke halaman ini. Untuk mantan Gubernur Alabama yang juga dijuluki The Love Gov, lihat Robert J. Bentley. Untuk pemain basket, lihat Mark Sanford (pemain basket). Untuk politikus Dakota Utara, lihat Mark Sanford (politikus Dakota Utara). Mark Sanford Gubernur Carolina Selatan ke-115Masa jabatan15 Januari 2003 – 12 Januari 2011WakilAndré Bauer PendahuluJim HodgesPenggantiNikki HaleyAnggota Dewan Perwakilan Rakyat A.S.dari dapil 1 South CarolinaMasa ja...

احتلال كوريتسا جزء من حرب البلقان الأولى التاريخ 20 ديسمبر 1912 الموقع كورتشي 40°36′50″N 20°46′40″E / 40.614025°N 20.777777777778°E / 40.614025; 20.777777777778 المتحاربون الدولة العثمانية مملكة اليونان تعديل مصدري - تعديل عنتمعارك حرب البلقان الأولىالجبهة الب...

1949 film by Nicholas Ray A Woman's SecretTheatrical release posterDirected byNicholas RayScreenplay byHerman J. MankiewiczBased onMortgage on Life1946 novelby Vicki BaumProduced byHerman J. MankiewiczStarringMaureen O'HaraMelvyn DouglasGloria GrahameCinematographyGeorge E. DiskantEdited bySherman ToddMusic byFriedrich HollaenderDistributed byRKO Radio PicturesRelease date February 7, 1949 (1949-02-07) (US)[1] Running time84 minutesCountryUnited StatesLanguageEnglis...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

EA-3887 Identifiers CAS Number 110913-97-8 3D model (JSmol) Interactive image InChI InChI=1S/C32H54N6O4.2BrH/c1-35(2)31(39)41-29-19-17-21-33-27(29)25-37(5,6)23-15-13-11-9-10-12-14-16-24-38(7,8)26-28-30(20-18-22-34-28)42-32(40)36(3)4;;/h17-22H,9-16,23-26H2,1-8H3;2*1H/q+2;;/p-2Key: DQBNOGPLNCQNRU-UHFFFAOYSA-L SMILES CN(C)C(=O)Oc1cccnc1C[N+](C)(C)CCCCCCCCCC[N+](C)(C)Cc2ncccc2OC(=O)N(C)C.[Br-].[Br-] Properties Chemical formula C32H54Br2N6O4 Molar mass 746.630 g·mol−1 Appearan...
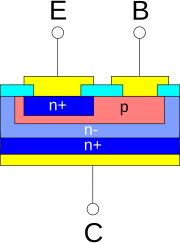
Electronic component that exploits the electronic properties of semiconductor materials For information on semiconductor physics, see Semiconductor. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Semiconductor device – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove thi...

American politician Norma PaulusSuperintendent of Public Instruction of OregonIn officeOctober 1, 1990 – January 4, 1999GovernorNeil GoldschmidtBarbara RobertsJohn KitzhaberPreceded byJohn EricksonSucceeded byStan Bunn20th Secretary of State of OregonIn officeJanuary 3, 1977 – January 7, 1985GovernorRobert StraubVictor AtiyehPreceded byClay MyersSucceeded byBarbara Roberts Personal detailsBornNorma Jean Petersen(1933-03-13)March 13, 1933Belgrade, Nebraska, U.S.DiedFebrua...
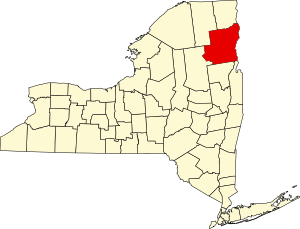
Location of Essex County in New York Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) List of the National Register of Historic Places listings in Essex County, New York. This is intended to be a complete list of properties and districts listed on the National Register of Historic Places in Essex County, New York, United States. The locations of National Register properties and districts (at least...

American philosopher (born 1947) Nancy FraserFraser in 2008Born (1947-05-20) May 20, 1947 (age 77)Baltimore, Maryland, USEra20th-century philosophyRegionWestern philosophySchoolContinental philosophyCritical theoryFeminist philosophyPost-MarxismPost-structuralismInstitutionsThe New SchoolMain interestsPolitical philosophy Nancy Fraser (/ˈfreɪzər/; born May 20, 1947) is an American philosopher, critical theorist, feminist, and the Henry A. and Louise Loeb Professor of Political and Soc...

MugeunjiNama KoreaHangul묵은지 Alih AksaraMugeunjiMcCune–ReischauerMuk'eunji Mukeunji adalah salah satu jenis kimchi yang terbuat dari sawi putih.[1] Makanan ini didapat dari kimchi yang dibiarkan terfermentasi untuk jangka waktu yang panjang pada suhu yang rendah.[2] Setidaknya kimchi harus berumur enam bulan untuk dapat disebut sebagai mukeunji.[2] Ada pula yang menyebut bahwa mukeunji haruslah kimchi yang berumur lebih dari setahun.[3] Sejarah Sejarah m...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento edizioni di competizioni calcistiche inglesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Second Division 1984-19...

Medical conditionPotassium-aggravated myotoniaOther namesPAM[1]This condition is inherited in an autosomal dominant manner myotonia figure.png Potassium-aggravated myotonia is a rare genetic disorder that affects skeletal muscle.[2] Beginning in childhood or adolescence, people with this condition experience bouts of sustained muscle tensing (myotonia) that prevent muscles from relaxing normally. Myotonia causes muscle stiffness, often painful, that worsens after exercise and ...

ColdrainIl gruppo in concerto nel 2017 Paese d'origine Giappone GenereAlternative metal[1]Post-hardcore[2][3]Metalcore[4][5] Periodo di attività musicale2007 – in attività EtichettaWarner Music Japan, VAP, Hopeless Records Studio7 Live5 Opere audiovisive8 Logo ufficiale Sito ufficiale Modifica dati su Wikidata · Manuale I Coldrain (コールドレイン?, Kōrudorein, stilizzato in coldrain) sono un gruppo musi...

German fairy tale For other uses, see Queen bee (disambiguation). The Queen BeeIllustration of the tale by Otto Ubbelohde.Folk taleNameThe Queen BeeAarne–Thompson groupingATU 554CountryGermanyPublished inGrimm's Fairy Tales The Queen Bee is a German fairy tale collected by the Brothers Grimm in Grimm's Fairy Tales (KHM 62). It is of Aarne-Thompson type 554 (The Grateful Animals).[1] Synopsis Two sons of a king went out to seek their fortunes, but fell into disorderly ways. The third...

日本でのアウトドアリビングの一例 ドイツのアウトドアリビングを持つ家 母屋から離れた庭の一角に東屋風の小さなリビングを設置したオーストラリアの例 日本の住宅事情でも視線を遮るアイテムの設置でアウトドアリビングを可能とした例。 アウトドアリビングとは、居間と隣接した庭やバルコニーなど、居間同様に生活空間として利用できるスペース。また、そ�...

2015年3月13日までの営業形態については「長野新幹線」をご覧ください。 北陸新幹線 北陸新幹線E7系電車(2020年8月、佐久平駅付近)基本情報国 日本所在地 群馬県、長野県、新潟県、富山県、石川県、福井県種類 高速鉄道(新幹線)起点 高崎駅終点 敦賀駅駅数 19駅開業 1997年10月1日(高崎駅 - 長野駅間)最終延伸 2024年3月16日(金沢駅 - 敦賀駅間)所有者 鉄道建設・�...

خريطة توضح أعداد المسيحيين اللاطائفيين في 2010 أكثر من 10 مليون أكثر من 1 مليون مسيحية لا طائفية (بالإنجليزية: Nondenominational Christianity) هُم المسيحيون الذين يصرحون بمسيحيتهم لكن يرفضون أن ينتموا إلى طائفة ويصنفون أيضاً كبروتستانت ويقولون أنهم مسيحيين بطريقتهم الخاصة م�...

1940 film The Man from NigerDirected byJacques de BaroncelliWritten byAlbert DieudonnéJoseph KesselAndré LegrandJean Paillard (books)StarringVictor FrancenJacques DumesnilAnnie DucauxCinematographyLéonce-Henri BurelEdited byJean SachaMusic byHenri TomasiProductioncompanySPFLHDistributed byLes Films BodaloRelease date 27 January 1940 (1940-01-27) Running time102 minutesCountryFranceLanguageFrench The Man from Niger or Forbidden Love (French: L'homme du Niger) is a 1940 French...
