Examples of vector spaces
|
Read other articles:

A.DeInformasi latar belakangAsalSeoul, Korea SelatanTahun aktif2016 – 2017Label2ABLE CompanyCJ E&MWarner Music KoreaMantan anggota Suyeon Yeorin Jiseo Rachel Haeyoung Choyoon Miso A.De (에이디이) adalah sebuah grup vokal perempuan beranggotakan tujuh orang yang berada di bawah label 2ABLE Company. Mereka debut pada 23 Juni 2016 dengan singel Strawberry. Anggota Suyeon (수연) - pemimpin, vokalis Yeorin (여린) - rapper, vokalis Jiseo (지서) - vokalis Rachel (라헬) - rapper Hae...

This article is part of a series aboutGeorge Washington Early life Family Military career Electoral history American Revolution Virginia Association Commander in Chiefof the Continental Army Valley Forge Battle of Trenton Mount Vernon Conference 1787 Constitutional Convention 1st President of the United States Presidency (Timeline) First term 1788–89 election 1st inauguration Judiciary Act Whiskey Rebellion Thanksgiving Presidential title Coinage Act Residence Act District of Columbia Seco...

Natrium bis(trimetilsilil)amida Nama Nama IUPAC Natrium bis(trimetilsilil)amida Nama lain natrium heksametildisilazana,natrium heksametildisilazida,NaHMDS Penanda Nomor CAS 1070-89-9 3DMet {{{3DMet}}} Nomor EC Nomor RTECS {{{value}}} CompTox Dashboard (EPA) DTXSID5061451 Sifat Rumus kimia C6H18NNaSi2 Massa molar 183,37 g/mol Penampilan zat padat berwarna keputihan Densitas 0,9 g/cm3, padat Titik lebur 171-175 °C (kira-kira 446 K) Titik didih 170 °C/...

Sensus Amerika Serikat ke-13 dilakukan oleh Biro Sensus tanggal 15 April 1910,[1] yang menetapkan jumlah penduduk Amerika Serikat adalah 92.228.496 jiwa, peningkatan 21.0 persen dari 76.212.168 jiwa yang dihitung selama Sensus 1900. Sensus 1910 berpindah dari orientasi kertas memanjang menjadi orientasi mendatar. Pertanyaan sensus Sensus 1910 mengumpulkan informasi berikut:[2] alamat nama hubungan dengan kepala keluarga jenis kelamin ras usia status nikah dan, bila menikah, la...

Palestinian attack on Israeli border post This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2006 Gaza cross-border raid – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this template message) 2006 Gaza cross-border raidPart of Gaza–Israel conflictTypeCross-border rai...

Maria José del BelgioMaria José del Belgio in un ritratto fotografico di Ghitta Carell del 1946Regina consorte d'ItaliaStemma In carica9 maggio 1946 –18 giugno 1946 PredecessoreElena del Montenegro SuccessoreMonarchia abolita Nome completofrancese: Marie-José Charlotte Sophie Amélie Henriette Gabrielleitaliano: Maria Giuseppina Carlotta Sofia Amelia Enrichetta Gabriella TrattamentoSua Maestà Altri titoliPrincipessa di Piemonte (1930-1946)Principessa del Belgio (1906-1930) Na...

Austrian-born British nuclear physicist Otto Robert FrischOBE FRSOtto Robert Frisch's wartime Los Alamos ID badge photoBorn(1904-10-01)1 October 1904Vienna, Austria-HungaryDied22 September 1979(1979-09-22) (aged 74)Cambridge, United KingdomNationalityAustrianCitizenshipAustriaUnited KingdomAlma materUniversity of ViennaKnown forAtomic bombAwardsFellow of the Royal Society[1]Scientific careerFieldsPhysics Signature Otto Robert Frisch OBE FRS[1] (1 October...

Questa voce o sezione sull'argomento grafemi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Ḫāʾ, o khāʾ (in arabo خاء? /xæ:ʔ/) è la settima lettera dell'alfabeto arabo. Nella numerazione abjad essa assumeva il valore di 600. Indice 1 Origine 2 Fonetica 3 Scrittura e traslitterazione 4 Sintassi 5 Altri progetti Origine Lo stesso a...

Public college in Buzzards Bay, Massachusetts This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Massachusetts Maritime Academy – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this message) Massachusetts Maritime AcademyFormer nameMassachusetts Nautical Training School...

1988 live album by Tom WaitsBig TimeLive album by Tom WaitsReleasedSeptember 1988RecordedNovember 5 and November 9, 1987VenueThe Warfield, San Francisco, and Wiltern Theatre, Los AngelesGenre Blues rock experimental rock Length64:15LabelIslandProducerChris BlackwellKathleen BrennanTom WaitsTom Waits chronology Franks Wild Years(1987) Big Time(1988) Night on Earth(1992) Tom Waits live chronology Big Time(1988) Romeo Bleeding: Live from Austin(2009) Singles from Big Time 16 Shells From ...

Traditional sub-divisions unique to the historic county of Sussex in England Rape of ArundelThe Norman Motte of Arundel Castle, once the administrative centre of the RapeThe Rape of Arundel shown within SussexArea • 1831132,800 acres (537 km2) Population • 180122,478 • 181124,276 • 183131,064 Density • 18310.23 inhabitants per acre (57/km2) History • Created6th to 11th century • Succeeded bySussex (w...
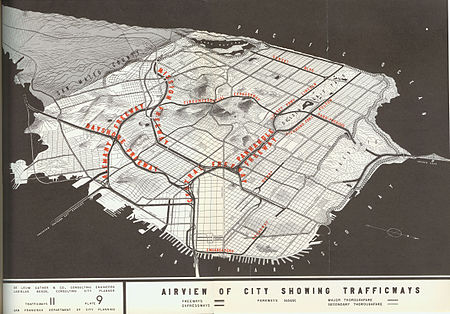
サンフランシスコの道路計画(1948年) 交通計画(こうつうけいかく、Transportation planning)とは交通工学に基づき交通の在り方について計画する学問である。交通バリアフリー法を受けての高齢化社会への対応・環境負荷の軽減などの新たな課題への対応も対象とされている。 交通の需要予測 手法は大きく集計型と非集計型の2つに分類される。 集計型でもっとも一般的な�...

Ларс Корвальднорв. Lars Korvald Премьер-министр Норвегии 18 октября 1972 — 16 октября 1973 Предшественник Трюгве Браттели Преемник Трюгве Браттели Рождение 29 апреля 1916(1916-04-29)Мьёндален, Недре-Эйкер, Норвегия Смерть 4 июля 2006(2006-07-04) (90 лет)Мьёндален, Недре-Эйкер, Норвегия Супруга Ruth ...

У этого топонима есть и другие значения, см. Вильфранш. КоммунаВильфранш-д’АльеVillefranche-d'Allier Герб 46°23′51″ с. ш. 2°51′29″ в. д.HGЯO Страна Франция Регион Овернь Департамент Алье Кантон Монмаро Мэр Bruno Rojouan(2008–2014) История и география Площадь 39,63 км² Высота центра 227�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2021) بيلي ارسي (بالإسبانية: Billy Vladimir Arce Mina) معلومات شخصية الميلاد 12 يوليو 1998 (العمر 26 سنة)إسمرالداس الطول 1.78 م (5 قدم 10 بوصة) مركز اللعب نصف الجناح ا...

Welcome Welcome! Hello, SciGal, and welcome to Wikipedia! Thank you for your contributions. I hope you like the place and decide to stay. Here are some pages that you might find helpful: The five pillars of Wikipedia Tutorial How to edit a page How to write a great article Manual of Style I hope you enjoy editing here and being a Wikipedian! Please sign your messages on discussion pages using four tildes (~~~~); this will automatically insert your username and the date. If you need help, che...

Ilustración de fuentes luminosas de magnitud 1 a 3,5, en incrementos de 0,5 En astronomía, la magnitud es la medida del brillo de una estrella. Los antiguos astrónomos griegos llamaban estrellas de primer tamaño (primera magnitud), a las estrellas más brillantes que aparecían después del ocaso solar y a las últimas que desaparecían tras la salida del Sol, y sucesivamente estrellas de segundo tamaño (segunda magnitud), tercera magnitud, etc., hasta las estrellas de sexta magnitud, la...

Questa voce o sezione sull'argomento trasporti non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento trasporti ha un'ottica geograficamente limitata. Contribuisci ad ampliarla o proponi le modifiche in discussione. Se la voce è approfondita, valuta se sia preferibile r...

Geographic region of Montenegro Geographic region of Montenegro in DalmatiaBay of Kotor Boka kotorskaБока которскаGeographic region of MontenegroView over Bay of Kotor Municipalities that form the Bay of Kotor region: Kotor, Herceg Novi and Tivat. Budva Municipality, historically considered a part of the Bay of Kotor region.Coordinates: 42°27′N 18°40′E / 42.45°N 18.67°E / 42.45; 18.67Country Montenegro CroatiaHistoric...

Highest Imperial Russian military rank Field marshal (General-feldmarshal, General-fel'dmarshal, General field marshal, or simply Fieldmarshal; Russian: Генерал-фельдмаршал) was, with the exception of Generalissimo, the highest military rank of the Russian Empire. It was a military rank of the 1st class in the Imperial Russian Army and equal to those of Chancellor and Active Privy Councillor, 1st class in civil service, and General Admiral in the Imperial Russian Navy.[1...
















