Read other articles:

Bukan Aku MenolakmuAlbum studio karya Dessy RatnasariDirilisJuni 1995GenrepopLabelBlackboardKronologi Dessy Ratnasari Lukisan Cinta (1993)String Module Error: Match not foundString Module Error: Match not found Bukan Aku Menolakmu (1995) Tenda Biru (1996)String Module Error: Match not foundString Module Error: Match not found Bukan Aku Menolakmu merupakan sebuah album kedua karya penyanyi sekaligus aktris Indonesia, Dessy Ratnasari. Album ini dirilis pada tahun 1995. Daftar lagu Bukan Aku...

Eccidi di San RuffilloTipofucilazione di massa Data10 febbraio - 17 aprile 1945 Luogo Stazione di Bologna San Ruffillo Rastignano, Pianoro Stato Italia ObiettivoPrincipalmente civili ResponsabiliGuardia Nazionale Repubblicana e SS MotivazioneEsecuzione di oppositori politici e partigiani ConseguenzeMortialmeno 133[1] Modifica dati su Wikidata · Manuale Gli eccidi di San Ruffillo si riferiscono ad una serie di fucilazioni di massa avvenute agli ordini delle forze nazifascist...

Women's elimination race at the 2023 UEC European Track ChampionshipsVenueTissot Velodrome, GrenchenDate9 FebruaryCompetitors16 from 16 nationsMedalists  Lotte Kopecky   Belgium Valentine Fortin   France Maike van der Duin   Netherlands← 20222024 → 2023 UEC EuropeanTrack ChampionshipsSprintmenwomenTeam sprintmenwomenTeam pursuitmenwomenKeirinmenwomenOmniummenwomenMadisonmenwomenTime trialmenwomenIndividual...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

AmaranthAlbum studio karya DavichiDirilis28 Januari 2008 (2008-01-28)3 Juli 2008 (Repackage)GenreK-popR&BBahasaKoreaLabelMnet Media (Core Contents Media dan Maroo Entertainment)Kronologi Davichi Amaranth(2008) Davichi in Wonderland(2009)Davichi in Wonderland2009 Singel dalam album Amaranth I Love You Even Though I Hate YouDirilis: 25 Januari 2008 Sad PromiseDirilis: 2 April 2008 Love and WarDirilis: 30 Juni 2008 Amaranth adalah album studio pertama dari duo asal Korea Selatan Dav...

Village in North Yorkshire, England Human settlement in EnglandBarton HillRoad junction in Barton HillBarton HillLocation within North YorkshireOS grid referenceSE707644Unitary authorityNorth YorkshireCeremonial countyNorth YorkshireRegionYorkshire and the HumberCountryEnglandSovereign stateUnited KingdomPost townYORKPostcode districtYO60PoliceNorth YorkshireFireNorth YorkshireAmbulanceYorkshire List of places UK England Yorkshire 54°04′17″N 0°55′12″W&#...

Ukrainian fact-checking organization StopFakeFormationMarch 2, 2014; 10 years ago (2014-03-02)FoundersMargot GontarOleg ShankovskyiYevhen Fedchenko (chief editor[1])Ruslan DeynychenkoPurposeFact-checkingHeadquartersKyiv, UkraineOfficial languages Russian, English, Spanish, Italian, Romanian, Bulgarian, French, Dutch, Czech, German[2]Staff (2022) 15Websitewww.stopfake.org The StopFake website is a project of Ukrainian media NGO Media Reforms Center. It was fou...

Rise in commodity prices in the early 2000s Fertilizer prices   DAP   Potassium chloride   Phosphorite   Triple Superphosphate   Urea The 2000s commodities boom or the commodities super cycle[1] was the rise of many physical commodity prices (such as those of food, oil, metals, chemicals and fuels) during the early 21st century (2000–2014),[2] following the Great Commodities Depression of the 1980s and 1990s. The boom was lar...

Ghassan MassoudPotret Ghassan Massoud dalam serial Drama - Unshoodat Al Matar, 2002Nama asalغسّان مسعودLahir20 September 1958 (umur 65)Damaskus, SuriahKebangsaanSuriahPekerjaanAktorTahun aktif1987–sekarangAnak2 Ghassan Massoud (Lahir 20 September 1958, Damaskus Kegubernuran Tartus, Suriah) adalah aktor dan pembuat film Suriah. Dia terkenal secara internasional karena perannya sebagai Saladin (Salahuddin Ayyubi) dalam film Kingdom of Heaven tahun 2005 karya Ridley S...

温贝托·德·阿连卡尔·卡斯特洛·布兰科Humberto de Alencar Castelo Branco第26任巴西總統任期1964年4月15日—1967年3月15日副总统若澤·馬利亞·奥克明前任拉涅里·馬齐利继任阿图尔·达科斯塔·伊·席尔瓦 个人资料出生(1897-09-20)1897年9月20日 巴西塞阿腊州福塔雷萨逝世1967年7月18日(1967歲—07—18)（69歲） 巴西塞阿腊州梅塞雅納墓地 巴西福塔雷薩卡斯特洛·布兰科陵寢[1]...

此條目可能包含不适用或被曲解的引用资料，部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队（军事） 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Para otros usos de este término, véase Russo. Vince Russo Russo en 2007.Nacimiento Nueva York, Nueva York22 de mayo de 1961 (62 años)Alma máter University of Southern IndianaNombres artísticos Vicious VincentVic VenomVince RussoMr. Wrestling IIIThe Powers That BePeso 86.14 kg (190 lb)Estatura 1,88 m (6′ 2″)Nacionalidad Estados UnidosEntrenador Johnny RodzEstadísticasDebut 1996[editar datos en Wikidata] Vincent James Vince Russo (Long Island, 22 de mayo...

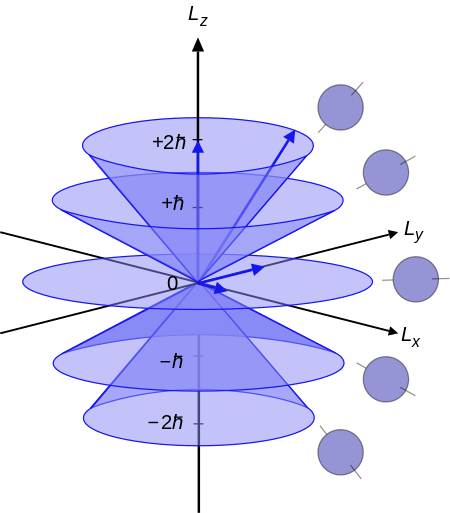
Bagian dari seri artikel mengenaiMekanika kuantum H ^ | ψ ( t ) ⟩ = i ℏ ∂ ∂ t | ψ ( t ) ⟩ {\displaystyle {\hat {H}}|\psi (t)\rangle =i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle } Persamaan Schrödinger Pengantar Glosarium Sejarah Buku teks Latar belakang Mekanika klasik Teori kuantum lama Notasi Bra–ket Hamiltonian Interferensi Dasar-dasar Bilangan kuantum Dekoherensi Fluktuasi kuantum Fungsi gelombang Keruntuhan fungsi gelo...

Cirolanidae Eurydice pulchra Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Subfilum: Crustacea Kelas: Malacostraca Ordo: Isopoda Subordo: Cymothoida Superfamili: Cymothooidea Famili: CirolanidaeDana, 1852 [1] Sinonim [1] Bathynomidae Wood Mason & Alcock, 1891 Cirolanidae adalah famili krustasea isopoda, yang terdiri dari predator dan scavenger yang aktif berenang dan memiliki mulut tipe pengigit.[2] Anggota cirolanidae termasuk genera berikut:&...

Artículo principal: Anexo:Fútbol en los XXIII Juegos Centroamericanos y del Caribe XXIII Juegos Centroamericanos y del CaribeColombia 2018 Torneo masculino Sede Colombia Colombia Fecha 20 de julio de 201831 de julio de 2018 Cantidad de equipos 8 Podio • Campeón• Subcampeón• Tercer lugar  01 ! COL Colombia02 ! VEN Venezuela03 ! HON Honduras Partidos 16 Goles anotados 42 (2,63 por partido) Goleador Julián Quiñones(4 goles) El fútbol ma...

Airline of the United States Contour Airlines IATA ICAO Callsign LF VTE VOLUNTEER Founded2016Commenced operationsMarch 22, 2016; 8 years ago (2016-03-22)AOC #FJTA920D[1]HubsCharlotteChicagoNashvillePhiladelphiaPhoenixSecondary hubsMacon[citation needed]Fleet size23Destinations28[2]Parent companyContour Aviation (75%)SkyWest, Inc. (25%)HeadquartersSmyrna, Tennessee, United StatesKey peopleMatt Chaifetz (CEO)[3]Websitecontourairlines.com C...

Biological process In the first stage of sexual reproduction, meiosis, the number of chromosomes is reduced from a diploid number (2n) to a haploid number (n). During fertilisation, haploid gametes come together to form a diploid zygote, and the original number of chromosomes is restored. Sexual reproduction is a type of reproduction that involves a complex life cycle in which a gamete (haploid reproductive cells, such as a sperm or egg cell) with a single set of chromosomes combines with ano...

Indonesia padaOlimpiade Musim Panas 2008Kode IOCINAKONKomite Olimpiade IndonesiaSitus webnocindonesia.idPenampilan pada Olimpiade Musim Panas 2008 di BeijingPeserta24 dalam 7 cabang olahragaPembawa benderaI Gusti Made Oka Sulaksana[1]MedaliPeringkat ke-42 1 1 4 Total 6 Penampilan pada Olimpiade Musim Panas (ringkasan)195219561960196419681972197619801984198819921996200020042008201220162020 Indonesia berlaga dalam Olimpiade Beijing 2008 yang dilangsungkan tanggal 8 sampai 24 Agustu...

Tactic in association football Program for an 1887 game between Blackburn Rovers and Sheffield Wednesday. The players of both teams are arranged in 2–3–5 formation. In association football, the formation of a team refers to the position players take in relation to each other on a pitch. As association football is a fluid and fast-moving game, a player's position (with the exception of the goalkeeper) in a formation does not define their role as tightly as that of rugby player, nor are the...

Abstraction of linear independence of vectors Not to be confused with Metroid or Meteoroid. In combinatorics, a branch of mathematics, a matroid /ˈmeɪtrɔɪd/ is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially order...