In mathematics, Casey's theorem, also known as the generalized Ptolemy's theorem, is a theorem in Euclidean geometry named after the Irish mathematician John Casey.

Let ${\displaystyle \,O}$ be a circle of radius ${\displaystyle \,R}$. Let ${\displaystyle \,O_{1},O_{2},O_{3},O_{4}}$ be (in that order) four non-intersecting circles that lie inside ${\displaystyle \,O}$ and tangent to it. Denote by ${\displaystyle \,t_{ij}}$ the length of the exterior common bitangent of the circles ${\displaystyle \,O_{i},O_{j}}$. Then:^[1]

${\displaystyle \,t_{12}\cdot t_{34}+t_{14}\cdot t_{23}=t_{13}\cdot t_{24}.}$

Note that in the degenerate case, where all four circles reduce to points, this is exactly Ptolemy's theorem.

The following proof is attributable^[2] to Zacharias.^[3] Denote the radius of circle ${\displaystyle \,O_{i}}$ by ${\displaystyle \,R_{i}}$ and its tangency point with the circle ${\displaystyle \,O}$ by ${\displaystyle \,K_{i}}$. We will use the notation ${\displaystyle \,O,O_{i}}$ for the centers of the circles. Note that from Pythagorean theorem,

${\displaystyle \,t_{ij}^{2}={\overline {O_{i}O_{j}}}^{2}-(R_{i}-R_{j})^{2}.}$

We will try to express this length in terms of the points ${\displaystyle \,K_{i},K_{j}}$. By the law of cosines in triangle ${\displaystyle \,O_{i}OO_{j}}$,

${\displaystyle {\overline {O_{i}O_{j}}}^{2}={\overline {OO_{i}}}^{2}+{\overline {OO_{j}}}^{2}-2{\overline {OO_{i}}}\cdot {\overline {OO_{j}}}\cdot \cos \angle O_{i}OO_{j}}$

Since the circles ${\displaystyle \,O,O_{i}}$ tangent to each other:

${\displaystyle {\overline {OO_{i}}}=R-R_{i},\,\angle O_{i}OO_{j}=\angle K_{i}OK_{j}}$

Let ${\displaystyle \,C}$ be a point on the circle ${\displaystyle \,O}$. According to the law of sines in triangle ${\displaystyle \,K_{i}CK_{j}}$:

${\displaystyle {\overline {K_{i}K_{j}}}=2R\cdot \sin \angle K_{i}CK_{j}=2R\cdot \sin {\frac {\angle K_{i}OK_{j}}{2}}}$

Therefore,

${\displaystyle \cos \angle K_{i}OK_{j}=1-2\sin ^{2}{\frac {\angle K_{i}OK_{j}}{2}}=1-2\cdot \left({\frac {\overline {K_{i}K_{j}}}{2R}}\right)^{2}=1-{\frac {{\overline {K_{i}K_{j}}}^{2}}{2R^{2}}}}$

and substituting these in the formula above:

${\displaystyle {\overline {O_{i}O_{j}}}^{2}=(R-R_{i})^{2}+(R-R_{j})^{2}-2(R-R_{i})(R-R_{j})\left(1-{\frac {{\overline {K_{i}K_{j}}}^{2}}{2R^{2}}}\right)}$

${\displaystyle {\overline {O_{i}O_{j}}}^{2}=(R-R_{i})^{2}+(R-R_{j})^{2}-2(R-R_{i})(R-R_{j})+(R-R_{i})(R-R_{j})\cdot {\frac {{\overline {K_{i}K_{j}}}^{2}}{R^{2}}}}$

${\displaystyle {\overline {O_{i}O_{j}}}^{2}=((R-R_{i})-(R-R_{j}))^{2}+(R-R_{i})(R-R_{j})\cdot {\frac {{\overline {K_{i}K_{j}}}^{2}}{R^{2}}}}$

And finally, the length we seek is

${\displaystyle t_{ij}={\sqrt {{\overline {O_{i}O_{j}}}^{2}-(R_{i}-R_{j})^{2}}}={\frac {{\sqrt {R-R_{i}}}\cdot {\sqrt {R-R_{j}}}\cdot {\overline {K_{i}K_{j}}}}{R}}}$

We can now evaluate the left hand side, with the help of the original Ptolemy's theorem applied to the inscribed quadrilateral ${\displaystyle \,K_{1}K_{2}K_{3}K_{4}}$:

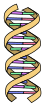
${\displaystyle {\begin{aligned}&t_{12}t_{34}+t_{14}t_{23}\\[4pt]={}&{\frac {1}{R^{2}}}\cdot {\sqrt {R-R_{1}}}{\sqrt {R-R_{2}}}{\sqrt {R-R_{3}}}{\sqrt {R-R_{4}}}\left({\overline {K_{1}K_{2}}}\cdot {\overline {K_{3}K_{4}}}+{\overline {K_{1}K_{4}}}\cdot {\overline {K_{2}K_{3}}}\right)\\[4pt]={}&{\frac {1}{R^{2}}}\cdot {\sqrt {R-R_{1}}}{\sqrt {R-R_{2}}}{\sqrt {R-R_{3}}}{\sqrt {R-R_{4}}}\left({\overline {K_{1}K_{3}}}\cdot {\overline {K_{2}K_{4}}}\right)\\[4pt]={}&t_{13}t_{24}\end{aligned}}}$

It can be seen that the four circles need not lie inside the big circle. In fact, they may be tangent to it from the outside as well. In that case, the following change should be made:^[4]

If ${\displaystyle \,O_{i},O_{j}}$ are both tangent from the same side of ${\displaystyle \,O}$ (both in or both out), ${\displaystyle \,t_{ij}}$ is the length of the exterior common tangent.

If ${\displaystyle \,O_{i},O_{j}}$ are tangent from different sides of ${\displaystyle \,O}$ (one in and one out), ${\displaystyle \,t_{ij}}$ is the length of the interior common tangent.

The converse of Casey's theorem is also true.^[4] That is, if equality holds, the circles are tangent to a common circle.

Casey's theorem and its converse can be used to prove a variety of statements in Euclidean geometry. For example, the shortest known proof^[1]: 411 of Feuerbach's theorem uses the converse theorem.

Wikimedia Commons has media related to Casey's theorem.

• Weisstein, Eric W. "Casey's theorem". MathWorld.
• Shailesh Shirali: "'On a generalized Ptolemy Theorem'". In: Crux Mathematicorum, Vol. 22, No. 2, pp. 49-53