Caratheodory-π solution
|
Read other articles:
Annual event held in Portland, OR This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (February 2021) (Learn how and when to remove this template message) This arti...

2006 children's novel This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The End novel – news · newspapers · books · scholar · JSTOR (December 2011) (Learn how and when to remove this template message) The End AuthorLemony Snicket (pen name of Daniel Handler)IllustratorBrett HelquistCountryUnited StatesLan...
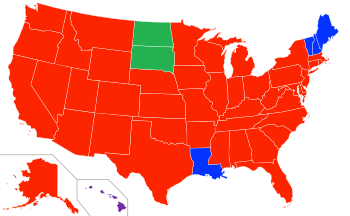
اللغات (2007) [1] الإنجليزية (فقط) 225.5 مليون الإسبانية بما فيها الكريولية 34.5 مليون الصينية 2.5 مليون الفرنسية بما فيها الكريولية 2 مليون التغالوغية 1.5 مليون الفيتنامية 1.2 مليون الألمانية 1.1 مليون الكورية 1.1 مليون اللغة الإنجليزية هي اللغة الوطنية بحكم الأمر الواقع في الولايا�...

Surface containing a line through every point Definition of a ruled surface: every point lies on a line In geometry, a surface S is ruled (also called a scroll) if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space. A ruled surface can be described as the set of points swept by ...

Tirunelveli Jn - Gandhidham JnHumsafar ExpressOverviewService typeHumsafar ExpressFirst service5 July 2018; 5 years ago (2018-07-05) (inaugural run)16 July 2018; 5 years ago (2018-07-16) (regular service)[1]Current operator(s)Western RailwaysRouteTerminiTirunelveli Junction (TEN)Gandhidham Junction (GIMB)Stops21Distance travelled2,400 km (1,491 mi)Average journey time45 hours 10 minsService frequencyWeekly [a]Train number(s)20923/...

Norwegian handball player (born 1990) Veronica Kristiansen Personal informationFull name Veronica Egebakken KristiansenBorn (1990-07-10) 10 July 1990 (age 33)Stavanger, NorwayNationality NorwegianHeight 1.75 m (5 ft 9 in)Playing position Left backClub informationCurrent club Győri ETO KCNumber 21Senior clubsYears Team2006–2009 Mjøndalen IF2009–2011 Vipers Kristiansand2011–2015 Glassverket IF2015–2018 FC Midtjylland2018– Győri ETO KCNational teamYears Team Apps...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

Armand Guy Simon de Coetnempren, conte di Kersaint Deputato all'Assemblea nazionale legislativaDurata mandato2 aprile 1792 –20 settembre 1792 Deputato alla Convenzione nazionaleDurata mandato14 settembre 1792 –18 gennaio 1793 Armand Guy Simon de Coetnempren, conte di KersaintNascitaParigi, 20 luglio 1742[1] MorteParigi, 6 settembre 1793 Cause della morteghigliottina Dati militariPaese servito Regno di Francia Forza armataMarine royale ArmaM...

جاك ريتشر: لا عودة مطلقاJack Reacher: Never Go Back (بالإنجليزية) معلومات عامةالصنف الفني حركة، جريمة، إثارةتاريخ الصدور 2016مدة العرض 118 دقيقة اللغة الأصلية الإنجليزيةمأخوذ عن Never Go Back (en) البلد الولايات المتحدةمواقع التصوير Lafayette Square (en) [1] — باتون روج[1] — نيو أورلينز[1] موقع...

Overview of the wildlife of the U.S. state of Alaska The wildlife of Alaska is both diverse and abundant. The Alaskan Peninsula provides an important habitat for fish, mammals, reptiles, and birds. At the top of the food chain are the bears. Alaska contains about 70% of the total North American brown bear population and the majority of the grizzly bears, as well as black bears and Kodiak bears. In winter, polar bears can be found in the Kuskokwim Delta, St. Matthew Island, and at the southern...

Yohanes BokakiusPekerjaanHumanis Renaisans, penulis, penyairKebangsaanItaliaPeriodeRenaisans Awal Yohanes Bokakius (Italia: Giovanni Boccaccio, antara Juni dan Juli 1313 - 21 Desember 1375) adalah penulis dan penyair Italia. Ia dilahirkan di Certaldo, Boccaccio dan tinggal di Firenze hingga usia 13 tahun kemudian pindah ke Napoli mengikuti ayahnya.[1] Dia adalah sahabat, murid, sekaligus koresponden Petrarca, seorang humanis Renaisans. Dia menulis sejumlah karya penting, termasuk Deca...

County in Idaho, United States Not to be confused with Teton, Idaho. County in IdahoTeton CountyCountyTeton County Courthouse SealLocation within the U.S. state of IdahoIdaho's location within the U.S.Coordinates: 43°45′N 111°13′W / 43.75°N 111.21°W / 43.75; -111.21Country United StatesState IdahoFoundedJanuary 26, 1915Named forThe Teton MountainsSeatDriggsLargest cityVictorArea • Total451 sq mi (1,170 km2) • Lan...

موقع السعودية التوقيت القياسي السعودي (بالإنجليزية: SAST) هو التوقيت المستخدم في السعودية، وهو يوافق التوقيت (ت ع م+03:00)، ويحتسب من خط طول 45° شرق. ظلت السعودية تستخدم التوقيت العربي حيث تحتسب الساعات منتصف الليل عند الغروب حتى عام 1968 حيث تم استخدام المنطقة الزمنية القياسية ا�...

Freeway Freeway, pseudonimo di Leslie Edward Pridgen (Filadelfia, 6 agosto 1978), è un rapper statunitense. È legato alla Roc-A-Fella Records di Jay-Z. Egli è famoso per le sue rime inserite all'interno dei versi e per la lunga barba che si lascia crescere in armonia con la sua fede nell'Islam. Egli ha preso il suo nome dal trafficante di droga Ricky Ross, simile ad un altro rapper, Rick Ross. Indice 1 Biografia 2 Discografia 2.1 Album in studio 2.2 Album collaborativi 2.3 EP 2.4 Mixtape 3...

Flooded sinkhole near the town of Hranice, Czech Republic Hranice Abyss Hranice Abyss (Czech: Hranická propast) is the deepest flooded pit cave in the world. It is a karst sinkhole near the town of Hranice, Czech Republic. The greatest confirmed depth is 519.5 m (1,704 ft), of which 450 m (1,476 ft) is underwater.[1][2] In 2020, a scientific expedition to the cave revealed that part of the system apparently reaches 1 kilometre deep, albeit with the lowest ...

American lawyer Silas StrawnPersonal detailsBornSilas Hardy Strawn(1866-12-15)December 15, 1866near Ottawa, Illinois, U.S.DiedFebruary 4, 1946(1946-02-04) (aged 79)Palm Beach, Florida, U.S.Resting placeLake Forest CemeteryPolitical partyRepublican Silas Hardy Strawn (December 15, 1866 – February 4, 1946) was a prominent Chicago lawyer and one of the name partners at the law firm of Winston & Strawn. He was also the president of the United States Chamber of Commerce during the e...

Commune in Bourgogne-Franche-Comté, FranceAllerey-sur-SaôneCommune Coat of armsLocation of Allerey-sur-Saône Allerey-sur-SaôneShow map of FranceAllerey-sur-SaôneShow map of Bourgogne-Franche-ComtéCoordinates: 46°54′23″N 4°59′00″E / 46.9064°N 4.9833°E / 46.9064; 4.9833CountryFranceRegionBourgogne-Franche-ComtéDepartmentSaône-et-LoireArrondissementChalon-sur-SaôneCantonGergyIntercommunalityCA Le Grand ChalonGovernment • Mayor (2020–...

Les troupes françaises en Chine désigne les unités françaises chargées de la défense militaire des concessions françaises en Chine. Elles prennent la suite en 1928 du corps d'occupation de Chine (COC), lui-même remplaçant en 1905 la brigade d'occupation de Chine. Cette dernière est créée en 1901 à partir du corps expéditionnaire français en Chine créé pour réprimer la révolte des Boxers. Historique Défilé des Renault FT de la compagnie de chars de Shanghai le 14 juillet 1...

Questa voce sull'argomento fisici tedeschi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Horst Ludwig Störmer Premio Nobel per la fisica 1998 Horst Ludwig Störmer (Francoforte sul Meno, 6 aprile 1949) è un fisico tedesco, vincitore, insieme a Daniel Tsui e Robert Laughlin, del premio Nobel per la fisica nel 1998, «per la scoperta di una nuova forma di fluido quantistico attraverso eccitazioni caricate frazionalmente» (effetto Hall quantisti...

Come leggere il tassoboxFunghiClassificazione scientificaDominioEukaryota (clade)Opisthokonta(Cavalier-Smith) Adl 2005 RegnoFungi Divisioni Ascomycota Basidiomycota Chytridiomycota Zygomycota Glomeromycota Cryptomycota[1] I funghi (Fungi, L. 1753, dal latino) o miceti[2] (dal greco antico μύκης?, mýkēs) sono un regno di organismi eucarioti, unicellulari e pluricellulari: comprende più di 700 000 specie conosciute, benché la diversità sia stata stimata in più di...
















