Calabi conjecture
|
Read other articles:

Kensington St Mary Abbots Church, dilihat dari Church St, sebelum persimpangan Kensington High Street Population 64,681 [1](sensus 2011) Ref. grid OS TQ255795 Borough London County seremonial Greater London Wilayah London Negara konstituen Inggris Negara berdaulat Britania Raya Kota pos LONDON Distrik kode pos SW5, SW7 Distrik kode pos W8, W14 Kode telepon 020 Polisi Metropolitan Pemadam kebakaran London Ambulans London Parlemen&...
Eglfing. Eglfing adalah kota yang terletak di distrik Weilheim-Schongau di Bayern, Jerman. Kota Eglfing memiliki luas sebesar 16.16 km². Eglfing pada tahun 2006, memiliki penduduk sebanyak 970 jiwa. lbsKota dan kotamadya di Weilheim-Schongau Altenstadt Antdorf Bernbeuren Bernried am Starnberger See Böbing Burggen Eberfing Eglfing Habach Hohenfurch Hohenpeißenberg Huglfing Iffeldorf Ingenried Oberhausen Obersöchering Pähl Peißenberg Peiting Penzberg Polling Prem Raisting Rottenbuch ...

Meiji Tokyo RenkaGambar visual kunci anime明治東亰恋伽(Meiji Tōkyō Renka)GenreRomantis PermainanPengembangBroccoliPenerbitBroccoliGenreNovel visualPlatformPlayStation PortableRilisJP: 26 September 2013 PermainanMeiji Tokyo Renka: Twilight Kiss (明治東亰恋伽 トワヰライト・キスcode: ja is deprecated )PengembangBroccoliPenerbitBroccoliGenreNovel visualPlatformPlayStation PortableRilisJP: 23 April 2015 Film animeGekijōban Meiji Tokyo Renka: Hanakagami no FantasiaSutradaraH...

Cal IsletIlhéu da CalCal Islet, viewed from Porto SantoLocation within the Municipality of Porto SantoGeographyLocationAtlantic OceanCoordinates33°00′32″N 16°23′13″W / 33.0089°N 16.3869°W / 33.0089; -16.3869Total islands1Area1.40 km2 (0.54 sq mi)Highest elevation178 m (584 ft)Concelhos (Municipalities)Porto SantoDemographicsPopulation0 Ilhéu de Baixo redirects here. For an island of the same name in the Azores, see Baixo Isle...

Filipina actress, columnist, editor, and lecturer This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelo...

Albert Plesman (1953) Albert Plesman (7 September 1889 – 31 Desember 1953) adalah seorang perintis dalam penerbangan Belanda dan administrator pertama dan kemudian direktur KLM, maskapai penerbangan tertua di dunia yang masih beroperasi dengan nama aslinya. Sampai kematiannya, ia bertanggung jawab sebagai direktur utama selama lebih dari 35 tahun dan juga di dewan maskapai penerbangan Belanda, yang menjadi salah satu maskapai terpenting di dunia di bawah kepemimpinannya. Ia la...

Bupati Sumba Barat DayaLambang Kabupaten Sumba Barat DayaPetahanaKornelius Kodi Metesejak 8 September 2019KediamanPendapa Kabupaten Sumba Barat DayaMasa jabatan5 tahunDibentuk22 Mei 2007Pejabat pertamaEmanuel Babu EhaSitus websbdkab.go.id Berikut ini adalah Daftar Bupati Sumba Barat Daya dari masa ke masa. No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati 1 Ir.Emanual Babu EhaM.Si. 22 Mei 2007 2008 1 [Ket. 1][1] 2 dr.Kornelius Kodi Mete 27 Desember 2008 27 Dese...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMA Negeri 1 JailoloInformasiJurusan atau peminatanIPA dan IPSRentang kelasX IPA, X IPS, XI IPA, XI IPS, XII IPA, XII IPSKurikulumKurikulum 2013AlamatLokasi, Jailolo, Maluku UtaraMoto SMA Negeri (SMAN) 1 Jailolo, merupakan salah satu Sekolah Menengah Ata...

The topic of this article may not meet Wikipedia's notability guideline for music. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Less Than an Hour – news · newspapers · books · scholar · JSTOR (April 20...
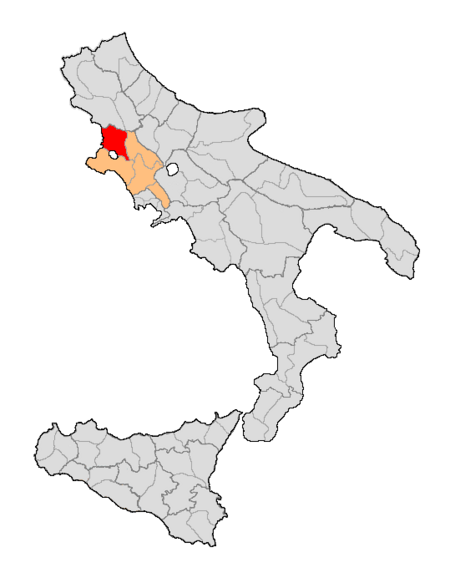
Voci principali: Storia di Sora, Sora (Italia). Distretto di SoraInformazioni generaliCapoluogoSora Dipendente da Terra di Lavoro Suddiviso in8 Circondari39 comuni16 villaggi AmministrazioneOrgani deliberativiSottintendenteConsiglio distrettuale Evoluzione storicaInizio1806 con Antonio Siciliani CausaL. 132 del 1806 del Regno di Napoli Fine1860 CausaOccupazione garibaldina e annessione al Regno di Sardegna. Preceduto da Succeduto da Circondario di Sora Cartografia Il distretto di Sora fu una...

内華達州 美國联邦州State of Nevada 州旗州徽綽號:產銀之州、起戰之州地图中高亮部分为内華達州坐标:35°N-42°N, 114°W-120°W国家 美國建州前內華達领地加入聯邦1864年10月31日(第36个加入联邦)首府卡森城最大城市拉斯维加斯政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])喬·隆巴爾多(R斯塔...

نيماها الإحداثيات 42°30′54″N 95°05′22″W / 42.515°N 95.089444444444°W / 42.515; -95.089444444444 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ساك خصائص جغرافية المساحة 0.190439 كيلومتر مربع (1 أبريل 2010) ارتفاع 403 متر عدد السكان عدد السكا�...

Former railway station in England HorfieldThe site in 2018General informationLocationBristol, City of BristolEnglandPlatforms4Other informationStatusDisusedHistoryOriginal companyGreat Western RailwayPost-groupingGreat Western RailwayKey dates14 May 1927Station opens23 November 1964Station closes vteRailways in the Bristol area Legend Cross Country Route Thornbury branch line Yate South Wales Main Line New Passage Pier Westerleigh Junction New Passage Halt Cross Hands Halt South Wales Ma...

聖若昂杜帕拉伊蘇(葡萄牙語:São João do Paraíso)是巴西的城鎮,位於該國東南部,由米納斯吉拉斯州負責管轄,始建於1944年1月1日,面積1,921平方公里,海拔高度1,073米,2010年人口23,309,人口密度每平方公里12.13人。 參見 米納斯吉拉斯州市鎮列表 參考資料 Frigoletto Statistics from IBGE (页面存档备份,存于互联网档案馆) Prefeitura Municipal[永久失效連結] 坐标:15°18′48�...

Cheikh BouamamaBorn1841[1][2]FiguigDiedOctober 7, 1908(1908-10-07) (aged 66–67)[3][4]Known forLeader of the tribe Awlad Sidi Shaykh Cheikh Bouamama or Shaykh Bu 'Amamah (Arabic: الشيخ بوعمامة) led a popular resistance against French occupation in Algeria from 1881 to 1908.[5] Cheikh Bouamama was a leader of the tribe Awlad Sidi Shaykh.[6] The resistance that he led in the southwest of Algeria from 1881 to 1908.[6]...

Peta langit di makam Senenmut, Wangsa XVIII[1] Astronomi Mesir bermula pada Zaman Prasejarah, dalam Zaman Prawangsa. Susunan batu-batu yang membentuk lingkaran di Nabta Playa dari milenium ke-5 SM diduga ditata menurut hasil perhitungan astronomi. Pada Zaman Sejarah, dalam Kurun Waktu Wangsa-Wangsa yang bermula pada milenium ke-3 SM, Kalender Mesir dengan 365 hari dalam setahun sudah dipergunakan, dan pengamatan bintang-bintang berperan penting dalam prakiraan banjir tahunan Sungai Ni...

Sporting event delegationBarbados at theParalympicsIPC codeBARNPCParalympic Association of BarbadosCompetitors1 in 1 sportsMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer appearances2000200420082012201620202024 Barbados first competed at the Paralympic Games in 2000. It has participated in five Summer Paralympics since then. The country has never taken part in the Winter Paralympics and has never won a Paralympic medal. Only two people have represented Barbados at the games: Daniel Coulthurst,...

1989 American filmA More Perfect UnionDVD and video coverDirected byPeter N. JohnsonScreenplay byTim SloverProduced byPeter N. Johnson Nicholas J. GasdikEdited byPeter G. CzernyMusic byKurt BestorProductioncompanyBrigham Young UniversityRelease date1989Running time112 minutesCountryUnited StatesLanguageEnglish A More Perfect Union: America Becomes a Nation is a 1989 American feature film dramatizing the events of the 1787 Constitutional Convention. The film was produced by Brigham Young Unive...

Sage 200Developer(s)Sage GroupInitial releaseApril 2002; 22 years ago (2002-04)Stable release2019 Operating systemMicrosoft WindowsTypeAccounting softwareLicenseProprietaryWebsitesage.com Sage 200 is a set of accountancy and management products developed by Sage Group aimed at medium enterprises. Sage offer different products under the Sage 200 name in different regions. The product name originally derives from the UK and Ireland version of the product where the number ...

Historical relationship between the Roman and Iranian empires Relations between the Roman and Iranian states were established c. 92 BC. It was in 69 BC that the two states clashed for the first time; the political rivalry between the two empires would dominate much of Western Asia and Europe until 628. Initially commencing as a rivalry between the Parthians and Rome, from the 3rd to mid-7th centuries the Roman Empire (later the Byzantine Empire) and its rival Sassanid Persia were recognized a...














