Blinding (cryptography)

In cryptography, blinding is a technique by which an agent can provide a service to (i.e., compute a function for) a client in an encoded form without knowing either the real input or the real output. Blinding techniques also have applications to preventing side-channel attacks on encryption devices.

More precisely, Alice has an input x and Oscar has a function f. Alice would like Oscar to compute y = f(x) for her without revealing either x or y to him. The reason for her wanting this might be that she doesn't know the function f or that she does not have the resources to compute it. Alice "blinds" the message by encoding it into some other input E(x); the encoding E must be a bijection on the input space of f, ideally a random permutation. Oscar gives her f(E(x)), to which she applies a decoding D to obtain D(f(E(x))) = y.

Not all functions allow for blind computation. At other times, blinding must be applied with care. An example of the latter is Rabin–Williams signatures. If blinding is applied to the formatted message but the random value does not honor Jacobi requirements on p and q, then it could lead to private key recovery. A demonstration of the recovery can be seen in CVE-2015-2141[1] discovered by Evgeny Sidorov.

A common application of blinding is in blind signatures. In a blind signature protocol, the signer digitally signs a message without being able to learn its content.

The one-time pad (OTP) is an application of blinding to the secure communication problem, by its very nature. Alice would like to send a message to Bob secretly, however all of their communication can be read by Oscar. Therefore, Alice sends the message after blinding it with a secret key or OTP that she shares with Bob. Bob reverses the blinding after receiving the message. In this example, the function f is the identity and E and D are both typically the XOR operation.

Blinding can also be used to prevent certain side-channel attacks on asymmetric encryption schemes. Side-channel attacks allow an adversary to recover information about the input to a cryptographic operation, by measuring something other than the algorithm's result, e.g., power consumption, computation time, or radio-frequency emanations by a device. Typically these attacks depend on the attacker knowing the characteristics of the algorithm, as well as (some) inputs. In this setting, blinding serves to alter the algorithm's input into some unpredictable state. Depending on the characteristics of the blinding function, this can prevent some or all leakage of useful information. Note that security depends also on the resistance of the blinding functions themselves to side-channel attacks.

For example, in RSA blinding involves computing the blinding operation E(x) = (xr)e mod N, where r is a random integer between 1 and N and relatively prime to N (i.e. gcd(r, N) = 1), x is the plaintext, e is the public RSA exponent and N is the RSA modulus. As usual, the decryption function f(z) = zd mod N is applied thus giving f(E(x)) = (xr)ed mod N = xr mod N. Finally it is unblinded using the function D(z) = zr−1 mod N. Multiplying xr mod N by r−1 mod N yields x, as desired. When decrypting in this manner, an adversary who is able to measure time taken by this operation would not be able to make use of this information (by applying timing attacks RSA is known to be vulnerable to) as she does not know the constant r and hence has no knowledge of the real input fed to the RSA primitives.

Examples

References

  1. ^ "CVE - CVE-2015-2141". cve.mitre.org. Retrieved 2023-12-13.

Read other articles:

Kijang Tumpuk

Kijang Tumpuk Jepara Kijang Tumpuk adalah sebuah karya seni ukir khas Jepara yang berkembang sejak zaman RA Kartini dan mengalami kejayaan selama kurang lebih satu abad sesudahnya. Kijang Tumpuk merupakan karya seni ukir yang paling disukai oleh pembeli dari dalam dan luar negeri. Bentuk Kijang Tumpuk berbentuk ukiran kayu yang di bentuk menyerupai Kijang yang bertumpuk-tumpuk secara vertikal, biasanya bahan yang digunakan adalah akar pohon baik pohon jati, maupun jenis pohon-pohon lain. Fung...

 

Swansea

Pour les articles homonymes, voir Swansea (homonymie). Swansea en gallois : Abertawe Les ruines du château de Swansea. Administration Pays Royaume-Uni Nation Pays de Galles Comté Swansea Statut Cité-comté (1er juin 2012[1]) Maire Sheigh Marjorie Spakowitz-Perdue (Parti travailliste gallois) Code postal SA1-SA7 Démographie Population 245 500 hab. (2016) Densité 649 hab./km2 Géographie Coordonnées 51° 37′ 00″ nord, 3° 57′ 00″ ...

 

نادي ميسان

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) ميسان الاسم الكامل نادي ميسان الرياضي اللقب الامير الملعب ملعب ميسان  البلد العراق  الدوري الدوري الع...

Ny-Friesland

Ny-Friesland is a peninsula located at the northern side of Spitsbergen, between Wijdefjorden and Hinlopen Strait. Newtontoppen, the highest mountain of Svalbard, is located at Ny-Friesland Ny-Friesland is the land area between Wijdefjorden and Hinlopen Strait on Spitsbergen, Svalbard.[1] The area is named after the Dutch province of Friesland.[2] References ^ Henriksen, Petter (ed.). Ny-Friesland. Store norske leksikon (in Norwegian). Oslo: Kunnskapsforlaget. Retrieved 13 Nov...

 

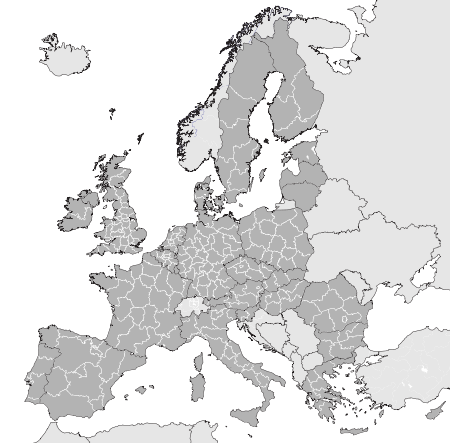
Nomenclatura delle unità territoriali statistiche

La nomenclatura delle unità territoriali statistiche, in acronimo NUTS (dal francese: Nomenclature des unités territoriales statistiques) identifica la ripartizione del territorio dell'Unione europea a fini statistici. Ideata dall'Eurostat nel 1988 tenendo come riferimento di base l'unità amministrativa locale, da allora è la principale regola per la redistribuzione territoriale dei fondi strutturali della UE, fornendo uno schema unico di ripartizione geografica, a prescindere dalle dimen...

 

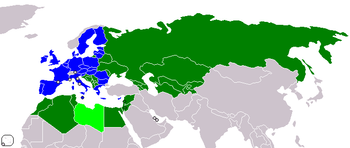
TEMPUS

For other uses, see Tempus (disambiguation).   EU Member states   TEMPUS partner countries   TEMPUS participation under discussion The TEMPUS (Trans-European Mobility Programme for University Studies) is a program that encouraged higher education institutions in the EU Member States and partner countries to engage in structured cooperation[1] through the establishment of consortia. The consortia implemented Joint European Projects (JEPs) with a clear set ...

Nicolò Tron

Disambiguazione – Se stai cercando Nicolò Tron (1685-1771), ambasciatore, politico e imprenditore veneto, vedi Nicolò Tron (politico e imprenditore). Questa voce o sezione sull'argomento sovrani italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Nicolò TronDoge di VeneziaStemma In carica1471 –1473 PredecessoreCristoforo Moro EredeFilipp...

 

Indiana's 10th congressional district

Former U.S. House district from 1843 to 2003 Indiana's 10th congressional districtObsolete districtCreated1840Eliminated2000Years active1843–2003 Indiana's 10th congressional district was a congressional district for the United States House of Representatives in Indiana. It encompassed roughly the Old City Limits of Indianapolis from 1983–2003. The district was re-drawn after the 1980 census and eliminated when Indiana's representation in the House of Representatives fell from 10 to n...

 

1952 United States presidential election in Connecticut

Election in Connecticut Main article: 1952 United States presidential election 1952 United States presidential election in Connecticut ← 1948 November 4, 1952 1956 →   Nominee Dwight D. Eisenhower Adlai Stevenson Party Republican Democratic Home state New York[1] Illinois Running mate Richard Nixon John Sparkman Electoral vote 8 0 Popular vote 611,012 481,649 Percentage 55.70% 43.91% County Results Municipality Results Eisenhower  &#...

Philippe V dari Spanyol

Philippe VRaja SpanyolBerkuasa1 Nopember 1700 – 14 Januari 1724(23 tahun, 74 hari)PendahuluCharles IIPenerusLouis IRaja SpanyolBerkuasa6 September 1724 - 9 Juli 1746(21 tahun, 306 hari)PendahuluLouis IPenerusFerdinand VIInformasi pribadiPemakamanLa Granja de San IldefonsoWangsaWangsa BourbonAyahLouis, Dauphin dari PrancisIbuMaria Anna Victoria dari BayernPasanganMaria Luisa dari SavoyElisabeth FarneseAnakRincianLouis I dari SpanyolFerdinand VI dari SpanyolCharles III dar...

 

约翰斯顿环礁

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌：《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

 

1642

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1642 – news · newspapers · books · scholar · JSTOR (January 2016) (Learn how and when to remove this message) Calendar year Millennium: 2nd millennium Centuries: 16th century 17th century 18th century Decades: 1620s 1630s 1640s 1650s 1660s ...

Bagaha Assembly constituency

Vidhan Sabha constituencyBagahaConstituency No. 4 for the Bihar Legislative AssemblyConstituency detailsCountryIndiaRegionEast IndiaStateBiharDistrictPaschim ChamparanLS constituency1. Valmiki NagarEstablished1957Total electors305,226ReservationNoneMember of Legislative Assembly17th Bihar Legislative AssemblyIncumbent Ram Singh PartyBJPAllianceNDAElected year2020 Bagaha Assembly constituency is an assembly constituency in Paschim Champaran district in the Indian state of Bihar. It was earlie...

 

不登校

この項目では、一般的な意味における不登校について説明しています。 在学者の不登校問題については「長期欠席」をご覧ください。 非在学者の不登校問題については「不就学」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検�...

 

Battle of Paoli

Battle of PaoliPart of the American Revolutionary WarA Dreadful scene of havock, a 1782 portrait depicting the Battle of PaoliDateSeptember 20, 1777LocationWillistown Township and Malvern, Pennsylvania, U.S.Result British victoryBelligerents  United States  Great BritainCommanders and leaders Anthony Wayne Charles GreyStrength 2,500 men 1,500 regulars 1,000 militia 1,200 men engaged600 in support 2 miles awayCasualties and losses 201 killed or wounded[1]71 captured [1 ...

Digital and Intelligence Service

Digital warfare branch of the Singapore Armed Forces Digital and Intelligence ServicePerkhidmatan Digital dan Perisikan (Malay)国防数码防卫与情报军部队 (Chinese)மின்னிலக்க, உளவுத்துறைப் படை (Tamil)Crest of the Digital and Intelligence ServiceFounded28 October 2022; 20 months ago (2022-10-28)Country SingaporeTypeCyber forceRoleHybrid warfarePart ofSingapore Armed ForcesMotto(s)Defend and Do...

 

نفط بحر الشمال

حقول النفط (باللون الأخضر) والغاز (باللون الأحمر) في بحر الشمال. نفط بحر الشمال هو خليط من الهيدروكربونات المكون من البترول السائل والغاز الطبيعي المنتج من مكامن البترول في بحر الشمال. في صناعة البترول، غالبًا ما يشمل مصطلح «بحر الشمال» مناطق مثل البحر النرويجي والمنطقة ال�...

 

Stasiun kereta api Mount Waverley

Mount WaverleyStasiun komuter PTVLokasiMiller Crescent, Mount WaverleyMelbourne, VictoriaAustraliaKoordinat37°52′31″S 145°07′42″E / 37.87528°S 145.12836°E / -37.87528; 145.12836PemilikVicTrackOperatorMetro TrainsJalur  Glen WaverleyJumlah peron2 sisiJumlah jalur2KonstruksiJenis strukturTanahParkir200Fasilitas sepeda12Informasi lainZona tarifMyki Zona 2Situs webPublic Transport VictoriaSejarahDibuka5 Mei 1930Operasi layanan Stasiun sebelumnya  ...

Koli Point action

1942 Allied victory over Japan on Guadalcanal Koli Point actionPart of the Pacific Theater of World War II75 mm pack howitzers of the 11th U.S. Marine Regiment fire in support of the operation against Japanese forces around Koli Point.Date3–12 November 1942LocationGuadalcanal, Solomon Islands9°27′S 160°10′E / 9.45°S 160.17°E / -9.45; 160.17Result Allied victoryBelligerents  United States  United Kingdom British Solomon Islands  Australia  ...

 

Batalha de Poitiers (732)

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW  • CAPES  • Google (N • L • A)). (Janeiro de 2011)  Nota: Se procura outras batalhas com o mesmo nome, veja Batalha de Poitiers. Batalha de Poitiers Data 10 de outubro de 732[1] Local Vouneuil-sur-Vienne, França Desfecho Vitória decisiva dos francos Beligerantes Reino FrancoFrância Ocidental Vascões Califado O...