Édouard Goursat
| |||||||||||||||||||||||||
Read other articles:

Negara-negara anggota NATO (biru), negara-negara dalam proses penyertaan ke NATO (biru muda), negara-negara yang mencari keanggotaan (ungu), dan CSTO yang dipimpin Rusia (merah). Hubungan antara Ukraina dan Pakta Pertahanan Atlantik Utara (NATO) berlangsung sejak 1990-an.[1] Meski bukan merupakan anggota dari NATO, Ukraina sempat menyatakan keinginannya untuk bergabung dengan NATO pada 2002.[2] Pada 2008, NATO menjanjikan Ukraina bergabung menjadi anggota pada suatu hari.[...

Stasiun Shiogama塩釜駅Stasiun Shiogama, April 2009Lokasi 5-1 Higashi-Tamagawa-cho, Shiogama-shi, Miyagi-ken 985-0042JepangKoordinat38°18′33″N 141°00′33″E / 38.3092°N 141.0092°E / 38.3092; 141.0092Koordinat: 38°18′33″N 141°00′33″E / 38.3092°N 141.0092°E / 38.3092; 141.0092Operator JR EastJalur ■ Jalur Utama Tōhoku ■ Jalur Senseki-Tōhoku Letak365.2 km dari TokyoJumlah peron1 peron pulauJumlah jalur2Informasi lain...

Distrik di KosovoKategoriDistrikLetakKosovo[a]Dibentuk olehKonstitusi KosovoJumlah wilayah7Penduduk174.235 (Peja) – 477.312 (Pristina)Luas1.000 km2 (400 sq mi) (Ferizaj) – 2.500 km2 (950 sq mi) (Pristina)Pembagian administratifMunisipalitas di Kosovo Distrik (bahasa Albania: Qark, atau Rajon; bahasa Serbia: Округ / Okrug atau Дистрикт / Distrikt atau Регион / Region)[1] adalah pembagian wilayah administratif ter...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. LââmLââm, 2013Informasi latar belakangLahir1 September 1971 (umur 52)AsalParis, PrancisGenrepop, soul, hip hopPekerjaanpenyanyiTahun aktif1998 – sekarangLabelHeben Music, Odeon, Sony/BMGSitus webwww.laam.net Lââm (lahir 1 September 1971) ...

The Nawab of Sardhana is an honorary Muslim title bestowed upon the descendants of the Afghan noble chieftain (nawab) and statesman Jan-Fishan Khan, for services to the British Raj – both in the failed British Afghan campaigns, as well as during the 1857 Rebellion in India. The hereditary title was once accompanied by a large jagir at Sardhana, made up largely of ancestral lands which once belonging to the Begum Samru. While these lands have mostly now been dispensed of, the descendants of ...

Pour les articles homonymes, voir Empire romain (homonymie) et Empire d'Occident. Empire carolingien 800–843/924Oriflamme de Charlemagne Monogramme autographe de Charlemagne. Étendue de l'Empire carolingien en Europe.Informations générales Statut Monarchie Capitale Metz, puis Aix-la-Chapelle Langue(s) Latin médiéval, ancien français, francique rhénan[1] Religion Christianisme Monnaie Denier d'argent Démographie Population < 30 000 000 habitants Superficie Superfic...

Georgia Secretary of StateGreat Seal of the State of GeorgiaIncumbentBrad Raffenspergersince January 14, 2019Term length4 yearsFirst holderJohn MiltonPosition Not to be confused with Minister of Foreign Affairs of Georgia. The Secretary of State of the U.S. state of Georgia is an elected official with a wide variety of responsibilities, including supervising elections and maintaining public records. The office has had a four-year term since 1946.[1] Before 1880, the secretary of ...

Poorest of the lower class in Naples during the Age of Revolution Lazzari playing cards, 1824 Look up lazzarone in Wiktionary, the free dictionary. In the Age of Revolution, the Lazzaroni (or Lazzari) of Naples were the poorest of the lower class (Italian lazzaroni or lazzari, singular: lazzarone) in the city and Kingdom of Naples (in present-day Italy). Described as street people under a chief, they were often depicted as beggars—which some actually were, while others subsisted partly by s...

القوات المسلحة للاتحاد الروسي شعار المتوسطة للقوات المسلحة للاتحاد الروسي راية للقوات المسلحة للاتحاد الروسي الدولة روسيا التأسيس 22 أكتوبر 1721[1][2]، و7 مايو 1992 الفروع القوات الجوية الروسيةالقوات البرية الروسيةالبحرية الروسية قوات الصواريخ الاستراتيجية...

Overview of American family models American family redirects here. For other uses, see American Family. An American family composed of the mother, father, children, and extended family The out of wedlock birth rates by race in the United States from 1940 to 2014. The rate for African Americans is the purple line. Data is from the National Vital Statistics System Reports published by the CDC National Center for Health Statistics. Note: Prior to 1969, African American illegitimacy was included ...

Miguel Layún Pemain Amerika Miguel Layun 2012Informasi pribadiNama lengkap Miguel LayúnTanggal lahir 25 Juni 1988 (umur 35)Tempat lahir Veracruz, MeksikoTinggi 180 cm (5 ft 11 in)Posisi bermain BekInformasi klubKlub saat ini VillarrealKarier senior*Tahun Tim Tampil (Gol)2018 – Villarreal 0 (0)Tim nasional2013 – Meksiko 67 (6) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Miguel Layún (lahir 25 Juni 1988) adalah seorang pemain sepak bola berk...

Aerial view of Opitsaht Opitsaht, spelled also as Opitsat and Opitsitah, is a Tla-o-qui-aht settlement/community in the Southwest area of the Meares Islands, Clayoquot South, British Columbia. This peninsula-like region is the home to the Tla-o-qui-aht people from the Nuu-chah-nulth nation, a tribe from the Pacific Northwest region in the lower Vancouver area, known for their lifestyle revolving around the marine life trade and culture within the community. During the era of the Maritime Fur ...

Village in Razavi Khorasan province, Iran For other places with the same name, see Shamabad. Village in Razavi Khorasan, IranShamabad Persian: شم ابادVillageShamabadCoordinates: 36°26′53″N 57°47′49″E / 36.44806°N 57.79694°E / 36.44806; 57.79694[1]CountryIranProvinceRazavi KhorasanCountyKhoshabDistrictNow Deh-e AnqolabRural DistrictTabasPopulation (2016)[2] • Total523Time zoneUTC+3:30 (IRST) Shamabad (Persian: شم اب...

River in New York, United States Map of the Croton River watershed The Croton River (/ˈkroʊtən/ KROH-tən) is a river in southern New York with three principal tributaries: the West Branch, Middle Branch, and East Branch. Their waters, all part of the New York City water supply system,[1] join downstream from the Croton Falls Reservoir.[a] Together, their waters and the reservoirs linked to them represent the northern half of the New York City water system's Croton Watershe...
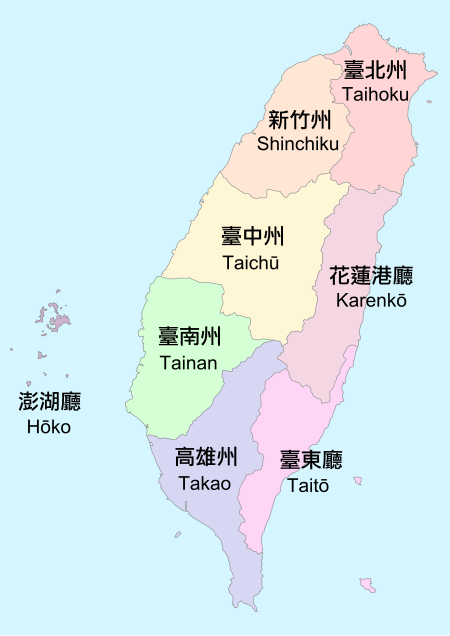
臺北州たいほくしゅう Taihoku Prefecture 日治臺灣的州1920年—1945年原臺北州廳舍,森山松之助設計,現由監察院使用。首府臺北市面积 • 1940年4,594.24平方公里(1,773.85平方英里)人口 • 1940年 1140530 歷史歷史 • 成立 1920年• 废除 1945年 行政分區3市 9郡 前身 继承 臺北廳 宜蘭廳 桃園廳 臺北縣 臺北市 (省轄市) 基隆市 今属于 中華民國(臺灣) 基�...

American radio personality Sam RobertsSam Roberts while working in the Opie and Anthony studio in 2005Birth nameSamuel Wood RobertsBorn (1983-09-06) September 6, 1983 (age 40)Medium Radio host television EducationSyracuse UniversityYears active2005–presentChildren3Notable works and rolesJim Norton & Sam Roberts Sam Roberts' Wrestling PodcastWebsitenotsam.com Samuel Wood Roberts (born September 6, 1983) is an American radio personality, podcast host, and WWE personality. Si...

Subfamily of mammals ReduncinaeTemporal range: Late Miocene to Present Kob Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Family: Bovidae Subfamily: ReduncinaeKnottnerus-Meyer, 1907 Genera Kobus Redunca Pelea The bovid subfamily Reduncinae or tribe Reduncini[1] is composed of nine species of antelope, all of which dwell in marshes, floodplains, or other well-watered areas, including the waterbucks and reedbucks.[2...

Dutch ship Duyfken The 1999 replica of Duyfken in 2006 History Dutch Republic NameDuyfken Launched1595 FateCondemned beyond repair July 1608 at Ternate General characteristics Displacement110 tons Length65.4 ft (19.9 m) Beam19.7 ft (6.0 m) Draft8 ft (2.4 m) PropulsionSail Speed7 knots (13 km/h; 8.1 mph) Armament8 cannons Duyfken (Dutch pronunciation: [ˈdœy̯f.kən]; Little Dove), also in the form Duifje or spelled Duifken or Duijfken...

Town and municipality in Northern Montenegro, MontenegroAndrijevica АндријевицаTown and municipalityChurch in Andrijevica Coat of armsAndrijevicaLocation of AndrijevicaCoordinates: 42°44′N 19°47′E / 42.73°N 19.79°E / 42.73; 19.79Country MontenegroRegionNorthern MontenegroMunicipality AndrijevicaGovernment • MayorŽeljko Ćulafić (SNP)Population (2023 census) • Rank22nd in Montenegro • Urban988 •&...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2024) (Learn how and when to remove this message) Elisabeth of HesseElisabeth with her husband, JohnBorn4 March 1502MarburgDied6 December 1557(1557-12-06) (aged 55)SchmalkaldenSpouseJohn of SaxonyHouseHouse of HesseFatherWilliam II of HesseMotherAnna of Mecklenburg-Schwerin Elisabeth of Hesse (4 March 1...




