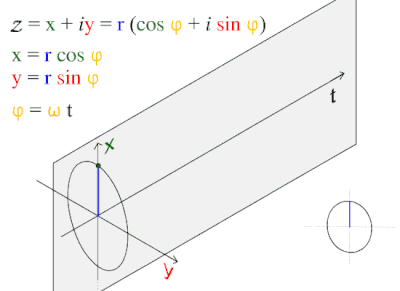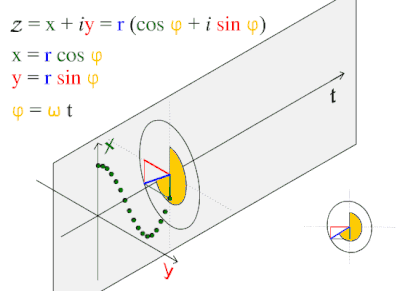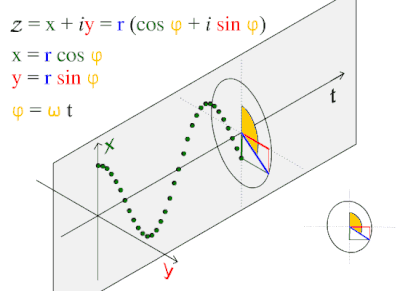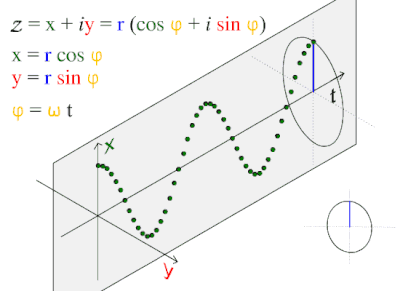
موجة جيبية
|
Read other articles:

Kepolisian MumbaiSingkatanमुं.पो.Mottoसद्रक्षणाय खलनिग्रहणाय (Sanskrit)Untuk melindungi Kebaikan dan untuk menghancurkan KejahatanIkhtisarDibentuk1661/1669[butuh rujukan]Struktur yurisdiksiWilayah hukumMumbai, INWilayah hukum Kepolisian MumbaiLuas wilayah6.034 km2 (2.330 sq mi)Populasi13,662,885Lembaga pemerintahDepartemen Dalam Negeri, Pemerintah MaharashtraKategoriPolisi sipil lokalLembaga sipil lokalMarkas besarKant...

Orde Serafim KerajaanKungliga SerafimerordenBintang ordeDianugerahkan oleh Raja SwediaTipeOrde jasa dengan satu tingkatanNegara SwediaMottoIesus Hominum Salvator (IHS)KelayakanKepala negara lain atau yang setara dan anggota Keluarga Kerajaan Swedia.Dianugerahkan kepadajasa kepada SwediaStatusKini dianugerahkanPenguasaRaja Carl XVI GustafKanselirSvante LindqvistTingkatKesatria(umum: RSerafO/LSerafO,Orang Swedia: RoKavKMO/LoKavKMO)StatistikPenganugerahan pertama1748, Frederick I dari Swedi...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2016) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. ...

نادي ديبورتيفو داس أيفيس تأسس عام 12 نوفمبر 1930 البلد البرتغال الدوري الدوري البرتغالي الممتاز الإدارة المدرب باولو فونسيكا (7 يونيو 2011–27 مايو 2012)أوغوستو إيناسيو (16 يناير 2019–21 أكتوبر 2019) الموقع الرسمي الموقع الرسمي الطقم الرسمي الطقم الأساسي الطقم الاحتياطي الطقم ال...

Chinese Main Battle Tank This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (October 2020) (Learn how and when to remove this template message) Type 59 A Type 59 tank in Military Museum of the Chinese People's RevolutionTypeMain battle tankPlace of originChinaService historyIn service1959–presentWarsVietnam WarSino-Indian WarIndo-Pakistani War of 1965Indo-Pakistani War of 1971Sin...

علم الأحياء البنيويصنف فرعي من علم الأحياء جزء من علم الأحياء الجزيئي يمتهنه structural biologist (en) تعديل - تعديل مصدري - تعديل ويكي بيانات علم الأحياء البنيوي أو البيولوجيا البنيوية هي فرع من فروع علم الأحياء الجزيئي والكيمياء الحيوية والفيزياء الحيوية والتي تهتم بدراسة البني...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Alessandro Rivali a Genova Alessandro Rivali (Genova, 5 aprile 1977) è un giornalista, scrittore e poeta italiano. Indice 1 Biografia 2 Opere 2.1 Poesia 2.2 Libri Intervista 2.3 A cura di 3 Note 4 Altri progetti Biografia Alessandro Rivali nasce il 5 aprile 1977 a Genova. Frequenta il liceo classico all'istituto Ravasco di Genova, dove si avvicina alla poesia scrivendone una, al posto del fratello, dedicata alla madre Fondatrice dell'ordine. Dopo il liceo si trasferisce a Milano e frequenta ...

Takeda Shingen in una rappresentazione artistica ad opera di Utagawa Kuniyoshi Takeda Shingen[1] (武田 信玄?; 1º dicembre 1521 – 13 maggio 1573) è stato un preminente daimyō giapponese del tardo periodo Sengoku, signore della provincia di Kai e uno dei condottieri di maggior prestigio del suo tempo. Soprannominato la tigre del Kai, legò indissolubilmente le sue gesta a quelle del clan Takeda, le quali vengono trattate nel Kōyō Gunkan. Indice 1 Nome 2 Biografia 2.1 Infanzia...

Cacia cretifera Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lamiinae Tribus: Mesosini Genus: Cacia Spesies: Cacia cretifera Cacia cretifera adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Cacia, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan ...

En la película Godzilla (1954) aparece el kaiju más famoso, Godzilla. Kaiju (怪獣, kaijū?) es una palabra japonesa que quiere decir 'bestia extraña' o 'bestia gigante', pero es generalmente traducido al español como 'monstruo'. Específicamente, esta palabra es usada para referirse a las gigantescas criaturas que atacan o protegen al mundo o la humanidad en el género tokusatsu (cine de acción con profusión de efectos especiales), y que son mayoritariamente originarias de Asia. Actua...

Village in County Wicklow, Ireland Village in Leinster, IrelandEnniskerry Áth na SceireVillageSaint Patrick's churchEnniskerryLocation in IrelandCoordinates: 53°11′34″N 6°10′14″W / 53.192768°N 6.170465°W / 53.192768; -6.170465CountryIrelandProvinceLeinsterCountyCounty WicklowElevation91 m (299 ft)Population (2022)2,008Irish Grid ReferenceO220174Websitewww.enniskerry.ie Enniskerry (historically Annaskerry, from Irish: Áth na Sceire, meaning ...

French luxury goods manufacturing company S.T. Dupont S.A.Company typePrivate (1872–1971) Subsidiary (1971–present)IndustryLuxury goodsFounded1872; 152 years ago (1872)FounderSimon Tissot-DupontFateAcquired by Gillette in 1971 Acquired by Dickson Concepts in 1987HeadquartersParis, FranceProductsBags, lighters, pens, watchesOperating incomeUSD 50 million [1][2] (1986)ParentDickson Concepts[3]Websitest-dupont.com S.T. Dupont is a French manufac...

Public school in Gloucestershire, England Cheltenham CollegeCheltenham College chapel and library (Big Modern)AddressBath RoadCheltenham, Gloucestershire, GL53 7LDEnglandCoordinates51°53′30″N 2°4′30″W / 51.89167°N 2.07500°W / 51.89167; -2.07500InformationTypePublic schoolPrivate boarding and day schoolMottoLatin: Labor omnia vincit(Work Conquers All)Religious affiliation(s)Church of EnglandEstablishedJuly 1841; 182 years ago (1841-07)...

Pyrrhus' campaigns in the Peloponnese Pyrrhus' invasion of the PeloponneseThe Siege of Sparta by Pyrrhus, by François Topino-LebrunDate272 BCLocationPeloponneseResult Macedonian and Spartan victoryTerritorialchanges Epirus loses control of Macedon and ThessalyBelligerents Epirus, Macedonia (Aeacid) Argive democratic faction Macedonia (Antigonid), Sparta, Messene, Argive oligarchic factionCommanders and leaders Pyrrhus of Epirus †, Ptolemy † Antigonus II Gonatas, Areus I...

Мостоукладчик СТ-26 (Сапёрный танк — 26 модель).ИТ-28, один из первых в мире танковых мостоукладчиков. МТУ, первый выпускавшийся крупносерийно в СССР танковый мостоукладчик. Танковый мостоукладчик, Мостовой танк[1][2] — боевая машина[1], специальный танк, бронир...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sukadana – news · newspapers · books · scholar · JSTOR (May 2011) (Learn how and when to remove this message) Town in West Kalimantan, IndonesiaSukadanaTownLiong Chinese dragon dance on the street of SukadanaCoordinates: 1°15′0″S 109°57′0″E / ...

United States Capitol cornerstone layingGeorge Washington depicted in a mural by Allyn CoxDateSeptember 18, 1793 (1793-09-18)VenueUnited States CapitolLocationWashington, D.C., U.S.Patron(s)George Washington The United States Capitol cornerstone laying was the Freemasonry ceremonial placement of the cornerstone of the United States Capitol on September 18, 1793. The cornerstone was laid by president of the United States George Washington Leder of the Lodge of the Continental A...

Este artículo se refiere o está relacionado con un evento deportivo de fútbol futuro. La información de este artículo puede cambiar frecuentemente. Por favor, no agregues datos especulativos y recuerda colocar referencias a fuentes fiables para dar más detalles. Copa Mundial Femenina de Fútbol Sub-20 2024FIFA U-20 Women's World Cup Colombia 2024 Estadio El Campín en Bogotá, sede de la final del torneo.Datos generalesSede Colombia ColombiaNombre completo Copa Mundial Femenina Su...

Калужское гетто Здания монастыря на улице Кооперативный посёлок, где располагалось гетто Тип закрытое Местонахождение Калуга Координаты 54°31′00″ с. ш. 36°16′00″ в. д.HGЯO Период существования 8 ноября — 30 декабря 1941 года Число узников 159 Число погибших 11 Председ...