دمق
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Eugenia GilbertGilbert dan Claire Adams di Man of the Forest (1921)LahirNovember 18, 1902East Orange, New JerseyMeninggalDecember 9, 1978 (usia 76)Santa Monica, CaliforniaNama lainEugenie GilbertPekerjaanAktrisTahun aktif1920–1929 (film) E...

Academy Awards ke-50TanggalSenin, 3 April 1978TempatDorothy Chandler Pavilion, Los AngelesPembawa acaraBob HopeProduserHoward W. KochPengarah acaraMarty PasettaSorotanFilm TerbaikAnnie HallPenghargaan terbanyakStar Wars Episode IV: A New Hope (7)Nominasi terbanyakJulia dan The Turning Point (11)Liputan televisiJaringanABCDurasi3 jam, 30 menitPeringkat39.73 juta31.1% (peringkat Nielsen)[1] ← ke-49 Academy Awards ke-51 → Academy Awards ke-50 diadakan di Dorothy Cha...

Nieuwe Rotterdamsche CourantEdisi tahun 1898, menampilkan Putri Wilhelmina dan ayahnyaTipeSurat kabar harianDidirikan1844Pandangan politikLiberalBahasaBelandaBerhenti publikasi1970PusatRotterdam Nieuwe Rotterdamsche Courant adalah sebuah surat kabar harian liberal yang berpusat di Rotterdam dan diterbitkan pada tahun 1844 hingga 1970. Sejarah Nieuwe Rotterdamsche Courant didirikan pada tahun 1844[1] oleh Henricus Nijgh. Pada tahun 1970, surat kabar ini digabungkan dengan surat kabar h...

RatahanKecamatanPeta lokasi Kecamatan RatahanNegara IndonesiaProvinsiSulawesi UtaraKabupatenMinahasa TenggaraPemerintahan • CamatArce Kalalo[1]Populasi (2021)[2] • Total13.910 jiwa • Kepadatan192/km2 (500/sq mi)Kode Kemendagri71.07.01 Kode BPS7109040 Luas72,30 km²Desa/kelurahan2 desa 9 kelurahan Ratahan adalah sebuah kecamatan yang berada di Kabupaten Minahasa Tenggara, provinsi Sulawesi Utara, Indonesia. Kecamatan Ratahan ju...

Behavioral paradigm in which organisms learn to predict aversive events Not to be confused with exposure therapy. Pavlovian fear conditioning is a behavioral paradigm in which organisms learn to predict aversive events.[1] It is a form of learning in which an aversive stimulus (e.g. an electrical shock) is associated with a particular neutral context (e.g., a room) or neutral stimulus (e.g., a tone), resulting in the expression of fear responses to the originally neutral stimulus or c...
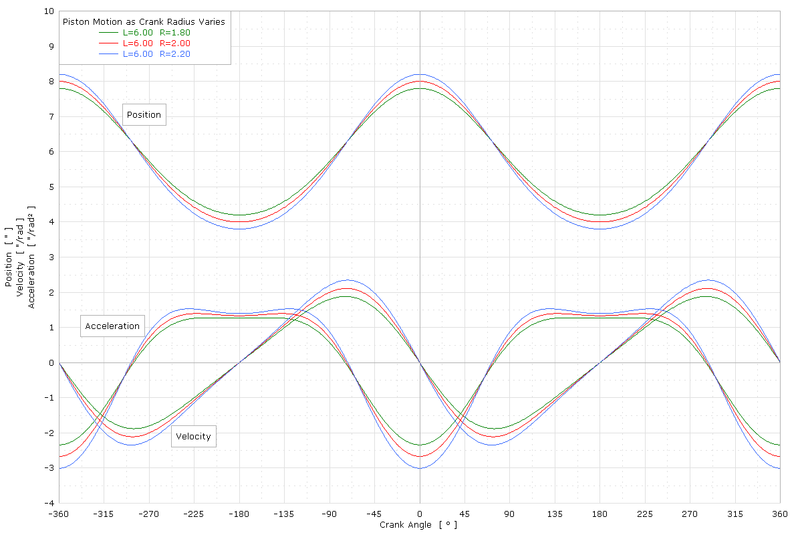
The reciprocating motion of a non-offset piston connected to a rotating crank through a connecting rod (as would be found in internal combustion engines) can be expressed by equations of motion. This article shows how these equations of motion can be derived using calculus as functions of angle (angle domain) and of time (time domain). Crankshaft geometry The geometry of the system consisting of the piston, rod and crank is represented as shown in the following diagram: Diagram showing geomet...

Villa RoseberyResidenza estiva delPresidente della Repubblica ItalianaAltri nomiVilla Maria Pia LocalizzazioneStato Italia RegioneCampania LocalitàNapoli IndirizzoVia Ferdinando Russo, 26 Coordinate40°48′02.18″N 14°12′17.9″E / 40.800605°N 14.204972°E40.800605; 14.204972Coordinate: 40°48′02.18″N 14°12′17.9″E / 40.800605°N 14.204972°E40.800605; 14.204972 Informazioni generaliCondizioniIn uso Costruzione1801-1857 Stileneoclassico UsoR...

Polish-born British activist Marion KozakBornDobra Jenta Kozak1934 (age 89–90)PolandAlma materLondon School of EconomicsPolitical partyLabourMovementJews for Justice for PalestiniansIndependent Jewish VoicesSpouseRalph MilibandChildrenDavid MilibandEd Miliband Marion Kozak or Marion Kozak Miliband (born 1934 as Dobra Jenta Kozak, also known as Maria Kozak) is a Polish-born British activist. She emigrated to the United Kingdom in the 1950s. In 1961, she married Ralph Miliband&#...

Lambang Komune Oissery. OisseryNegaraPrancisArondisemenMeauxKantonDammartin-en-GoëleAntarkomuneCommunauté de communes du Pays de la Goële et du MultienPemerintahan • Wali kota (2008-2014) Jean-Louis Chauvet • Populasi12.232Kode INSEE/pos77344 / 2 Population sans doubles comptes: penghitungan tunggal penduduk di komune lain (e.g. mahasiswa dan personil militer). Oissery merupakan sebuah komune di departemen Seine-et-Marne di region Île-de-France di utara-tengah...

Brazilian pianist Marcelo Bratke Marcelo Bratke (born September 6, 1960) is a Brazilian pianist. Career Bratke began his piano studies at the age of 14 with Zélia Deri.[1] Two years later he debuted with the São Paulo State Symphony Orchestra (OSESP) under the baton of conductor Eleazar de Carvalho, receiving the Revelation Pianist Award from the APCA (São Paulo State Association of Art Critics).[2] He made his European debut at the Salzburg Festival in 1988[3] and ...

Cream-filled pastry For other uses, see Éclair (disambiguation). Chocolate Eclair redirects here. For the Canadian drama film, see Chocolate Eclair (film). ÉclairÉclairs at Fauchon in ParisTypePastryPlace of originFranceAssociated cuisineFrench cuisineMain ingredientsChoux pastry, flavoured cream filling, icing Cookbook: Éclair Media: Éclair A classic éclair An éclair (English: /ɪˈklɛər/ ⓘ ih-KLAIR[1] or /eɪˈklɛər/ ay-KLAIR,[2] French: [eklɛ...

StarfleetAktif2130s–32nd century (latest date known)Negara United Federation of PlanetsTipe unitOrganisasi paramiliterPasukan antariksaBadan antariksaPeranPertahananKeamanan internalPemeliharaan perdamaianPenegakan hukumPertahanan sipilPenjelajahan antariksaPenelitian ilmiahDiplomasiMarkasSan Francisco, California, United Earth (2130-2381), Markas Federasi (2382-)PertempuranKonflik XindiPerang Bumi-RomulanPerang Klingon-FederasiPerang Federasi-TzenkethiPerang Federasi-CardassianKonflik perb...

Historically black university in Tuskegee, Alabama, US Tuskegee UniversityFormer namesTuskegee Normal School for Colored Teachers (1881–1891)Tuskegee Normal and Industrial Institute (1891–1937)Tuskegee Institute (1937–1985)[1]MottoScientia Principatus OperaMotto in EnglishKnowledge, Leadership, ServiceTypePrivate historically black land-grant universityEstablishedJuly 4, 1881; 142 years ago (1881-07-04)AccreditationSACSAcademic affiliationsNAICU[2]...

Royal Horse GuardsLivgarden til HestRoyal Horse Guards at Korsør on the way to the front line in Schsleswig during the First Schleswig War in 1848. Painting by Otto Bache from 1888.ActiveJanuary 1661−31 May 1866 (205 years, 4 months)Country DenmarkBranch Royal Danish ArmyTypeCavalryRoleGuard and escort dutySize675 men at its height in 1714Part ofRoyal Life GuardsGarrison/HQHestegardekassernen[1]Engagements The Battle of Helsingborg in 1710 The Battle of Gadebusc...

Conca dei MariniKomuneComune di Conca dei MariniLokasi Conca dei Marini di Provinsi SalernoNegaraItaliaWilayah CampaniaProvinsiSalerno (SA)Luas[1] • Total1,13 km2 (0,44 sq mi)Ketinggian[2]400 m (1,300 ft)Populasi (2016)[3] • Total730 • Kepadatan650/km2 (1,700/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos84010Kode area telepon089Situs webhttp://www.concadeimarini.org...

Cục Điều tra Hình sựQuân đội Nhân dân Việt NamQuân kỳQuân hiệuQuốc gia Việt NamThành lập19 tháng 11 năm 1948; 75 năm trước (1948-11-19)Phân cấpCục chức năng (Nhóm 3)Nhiệm vụLà cơ quan tham mưu chiến lược đầu ngành về công tác điều tra hình sự trong Quân độiBộ phận của Bộ Quốc phòngBộ chỉ huy14A8, Lý Nam Đế, quận Hoàn Kiếm, Hà NộiChỉ huyCục trưởng Nguyễn Thanh Huyxts ...

British politician (born 1979) The Right HonourableRachel ReevesMPOfficial portrait, 2024Chancellor of the ExchequerIncumbentAssumed office 5 July 2024Prime MinisterKeir StarmerPreceded byJeremy HuntChair of the Business, Energy and Industrial Strategy CommitteeIn office12 July 2017 – 7 April 2020Preceded byIain WrightSucceeded byDarren Jones Shadow portfolios 2021–2024Chancellor of the Exchequer2020–2021Duchy of Lancaster2020–2021Cabinet Office2013–2015Work and Pension...

Indian government plan for urban development Smart Cities MissionCountryIndiaPrime Minister(s)Narendra ModiMinistryMinistry of Urban DevelopmentKey peopleHardeep Singh Puri, Minister of Housing and Urban Affairs Kunal Kumar (Mission Director)[1]Launched2015; 9 years ago (2015)Funding₹203,979 crore (US$24 billion)[2]Websitesmartcities.gov.in Smart pole in Vizag setup as part of Smart Cities mission National Smart Cities Mission is an urban renewal and r...

French writer (1786 - 1866) Elise VoiartVoiart in 1811BornAnne-Élisabeth-Élise Petitpain10 February 1786 (1786-02-10)Nancy, FranceDied22 January 1866(1866-01-22) (aged 79)Nancy, FranceOccupation(s)Writer, translator, salon-holderSpouseJacques Philippe VoïartChildren3 including Amable Tastu, Élisabeth Voïart Élise Voïart, (1786-1866) was a writer and translator from Nancy, France, specializing in historical works, fiction and children's books. She held literary salons at her h...
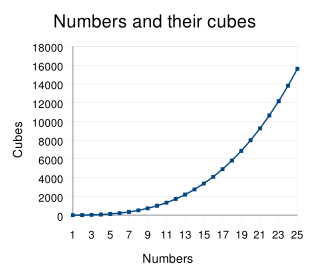
Un cubo perfetto è un qualsiasi numero naturale la cui radice cubica corrisponde ad un numero intero. y=x³, per valori interi 1≤x≤25. In aritmetica e algebra, il cubo di un numero n è la sua terza potenza, cioè il risultato della moltiplicazione del numero per sé stesso tre volte: n3 = n × n × n. Si tratta anche della formula per calcolare il volume di un cubo il cui lato ha una lunghezza pari a n. Da qui il nome. La funzione inversa di trovare il numero il cui cubo è n è...



