Read other articles:

Cica-kopi melayu Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passeriformes Famili: Timaliidae Genus: Pomatorhinus Spesies: P. montanus Nama binomial Pomatorhinus montanusHorsfield, 1821 Cica-kopi melayu (bahasa Latin: Pomatorhinus montanus) adalah spesies burung dari keluarga Timaliidae, dari genus Pomatorhinus. Burung ini merupakan jenis burung pemakan buah-buahan, kumbang, laba-laba, belalang, u...

Autobahn beralih ke halaman ini. Untuk kegunaan lain, lihat Autobahn (disambiguasi). Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Autobahn di Jerman – berita · surat kabar · buku · cendekiawan · JSTOR (July 2010) Markah autobahn Jerman Peta jaringan aut...

Asosiasi Baja DuniaSingkatanworldsteelTanggal pendirian10 Juli 1967TipeKelompok perdagangan industriKantor pusatBrussels, BelgiaLokasiBrusselsTokoh pentingChairman 2020-2021:YU Yong, HBIS Group Vice Chairmen 2020-2021: André JOHANNPETER, Gerdau Sajjan JINDAL, JSW Steel Treasurer 2020-2021: Mark VASSELLA, BlueScope Steel Limited Chairman of the International Stainless Steel Forum (ISSF):Bernardo VELÁZQUEZ, ACERINOXSitus webwww.worldsteel.org Asosiasi Baja Dunia, sering disebut worldsteel, ad...

Schillmöller di Sydney, Australia Mayor KNIL B.F.A. Ben Schilmöller, adalah seorang perwira militer Belanda yang pernah menjadi Komandan Militer Karesidenan Manado, sekaligus menjadi pemimpin pasukan tentara Hindia Belanda dalam Pertempuran Manado melawan Jepang, yang berlangsung pada tanggal 11 hingga 13 Januari 1942. Pendudukan Jepang di Indonesia Pertempuran Manado Di Manado, jumlah pasukan di bawah pimpinannya mencapai sekitar 1500 orang yang terbagi dalam tujuh divisi.[1] Denga...

1978 film by Michael Schultz Sgt. Pepper's Lonely Hearts Club BandTheatrical release posterDirected byMichael SchultzWritten byHenry EdwardsBased onSgt. Pepper's Lonely Hearts Club Bandby The BeatlesProduced byRobert StigwoodStarring Peter Frampton The Bee Gees Frankie Howerd Paul Nicholas Donald Pleasence Sandy Farina Dianne Steinberg Steve Martin Aerosmith Alice Cooper Earth, Wind & Fire Billy Preston George Burns Carel Struycken Narrated byGeorge BurnsCinematographyOwen RoizmanEdited b...

لو مان (بالفرنسية: Le Mans)‏[1](بالفرنسية: arrondissement du Mans)‏[1]   خريطة الموقع تقسيم إداري البلد فرنسا  [2] العاصمة لو مان التقسيم الأعلى سارت  خصائص جغرافية إحداثيات 48°00′06″N 0°12′01″E / 48.00177°N 0.2003°E / 48.00177; 0.2003 [3]  [4] المساحة 837 كيلومتر مربع&...

RamotLingkunganNegara IsraelProvinsiYerusalemKotaYerusalemZona waktuUTC+3 (EAT) • Musim panas (DST)UTC+3 (EAT) Ramot adalah sebuah lingkungan di kota suci Yerusalem di Distrik Yerusalem, tepatnya di sebelah timur Israel.[1] Tempat lain bernama sama Dalam Alkitab Ibrani atau Perjanjian Lama di Alkitab Kristen disebutkan kota kuno Ramot di wilayah suku Isakhar (1 Tawarikh 6:73).[2] Referensi ^ National Geospatial-Intelligence Agency. GeoNames database entry. (se...

Alumni houseAlumni House, 2020.General informationLocationWilliamsburg, VirginiaCountryUnited States of AmericaConstruction started1850s (original)2018 (reconstruction)Completed2020OwnerCollege of William and Mary in Virginia Part of a series on theCampus of theCollege of William & Mary Historic Campus (College Yard)Wren BuildingBraffertonPresident's House Old CampusAlumni HouseTucker HallBlow HallEwell HallSunken GardenCrim Dell bridgeHearth: Memorial to the Enslaved New CampusPhi Beta ...

Pic Glacier Vue du pic Glacier depuis le nord-est. Géographie Altitude 3 213 m[1] Massif North Cascades(chaîne des Cascades) Coordonnées 48° 06′ 43″ nord, 121° 06′ 47″ ouest[2],[1] Administration Pays États-Unis État Washington Comté Snohomish Ascension Première juin 1897 par Darcy Bard, A.H. Dubor, Thomas Gerdine et Sam Strom[3] Voie la plus facile Face sud Géologie Âge Pléistocène Roches Dacite andésitique Type Volcan de subduct...

Incidental music composed by Ludwig van Beethoven for Johann Wolfgang von Goethe's 1787 play Count of Egmont Overture from Egmont (9:01) Problems playing this file? See media help. Egmont, Op. 84 by Ludwig van Beethoven, is a set of incidental music pieces for the 1787 play of the same name by Johann Wolfgang von Goethe.[1] It consists of an overture followed by a sequence of nine pieces for soprano, male narrator, and full symphony orchestra. The male narrator is optional; he is not ...

Ball of crab meat deep-fried in batter Crab puffCrab puffs on traysCourseHors d'oeuvrePlace of originUnited StatesMain ingredientsCrab meat A crab puff is a ball of crab meat, mixed with flour, egg, and seasonings, that has been deep-fried in batter.[1][2] They are often served in restaurants as an appetizer or side dish.[3] They may be served alone, or with any of a variety of sauces, such as tartar sauce, cocktail sauce, or sweet and sour sauce. See also Crab rangoon...

拉米兹·阿利雅Ramiz Alia第1任阿尔巴尼亚總統任期1991年4月30日—1992年4月9日继任萨利·贝里沙阿尔巴尼亚人民议会主席团主席任期1982年11月22日—1991年4月30日前任哈奇·列希继任转任总统阿尔巴尼亚劳动党第一书记任期1985年4月13日—1991年5月4日前任恩维尔·霍查继任无（政党解散） 个人资料出生(1925-10-18)1925年10月18日 阿尔巴尼亚斯库台逝世2011年10月17日(2011歲—10—17)（85�...

Scandinavian caviar substitute The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Smörgåskaviar – news · newspapers · books · scho...

2010 Maldivian drama film NiumaOfficial film posterDirected byNiuma MohamedWritten byNiuma MohamedAbdulla MuazScreenplay byIbrahim WaheedProduced byMohamed AbdullaStarringNiuma MohamedYoosuf ShafeeuMohamed ManikAhmed NimalSheela NajeebCinematographyIbrahim MoosaEdited byAbdulla MuazMusic byMohamed IkramProductioncompanyDhekedheke Ves ProductionRelease date 25 October 2010 (2010-10-25) CountryMaldivesLanguageDhivehi Niuma is a 2010 Maldivian drama film directed by Niuma Mohamed....

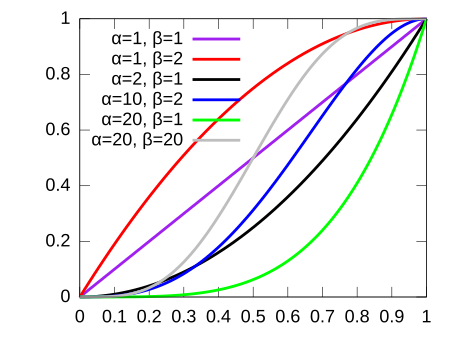
Model in population genetics Balding-Nichols Probability density function Cumulative distribution functionParameters 0 < F < 1 {\displaystyle 0<F<1} (real) 0 < p < 1 {\displaystyle 0<p<1} (real) For ease of notation, let α = 1 − F F p {\displaystyle \alpha ={\tfrac {1-F}{F}}p} , and β = 1 − F F ( 1 − p ) {\displaystyle \beta ={\tfrac {1-F}{F}}(1-p)} Support x ∈ ( 0 ; 1 ) {\displaystyle x\in (0;1)\!} PDF x α − 1 ( ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) بطولة أوروبا لكرة الطائرة للرجال 1985 تفاصيل الموسم بطولة أمم أوروبا للكرة الطائرة للرجال  النسخة 14  �...

Chemical compound VorapaxarClinical dataTrade namesZontivityOther namesSCH-530348Routes ofadministrationBy mouthATC codeB01AC26 (WHO) Legal statusLegal status CA: ℞-only[1] US: ℞-only Pharmacokinetic dataBioavailability~100%[2]Protein binding≥99%Metabolismhepatic (CYP3A4 and CYP2J2)Elimination half-life5–13 daysExcretionfeces (58%), urine (25%)Identifiers IUPAC name Ethyl N-[(3R,3aS,4S,4aR,7R,8aR,9aR)-4-[(E)-2-[5-(3-fluorophenyl)-2-pyridyl]vinyl]-3...

American author and activist (1952–2021) For the mixtape, see bell hooks (mixtape). bell hooksbell hooks in October 2014BornGloria Jean Watkins(1952-09-25)September 25, 1952Hopkinsville, Kentucky, U.S.DiedDecember 15, 2021(2021-12-15) (aged 69)Berea, Kentucky, U.S.EducationStanford University (BA)University of Wisconsin–Madison (MA)University of California, Santa Cruz (PhD)Occupations author academic activist Years active1978–2018Known forOppositional gazeNotable work Ain...

Corporal E. Hopwood of Acton, Wrexham, studies the Sunday Dispatch before voting in Egypt in the United Kingdom general election of 1945. The Sunday Dispatch was a prominent British newspaper, published between 27 September 1801 and 18 June 1961.[1][2] It was ultimately discontinued due to its merger with the Sunday Express.[3] History The newspaper was first published as the Weekly Dispatch in 1801, and was owned in the mid-1800s by notable solicitor James Harmer, who...

ポータル ディズニー ザ・リプレイス 大人とりかえ作戦ジャンル アニメーションコメディ出演者 ナンシー・カートライトグレイ・デリスルキャサリン・スーシーデヴィッド・マッカラムジェフ・ベネットローレン・トムエリカ・ハバードタラ・ストロングディー・ブラッドリー・ベイカー製作制作 Disney Channel 放送放送国・地域 アメリカ合衆国 日本放送期間2006年-2...