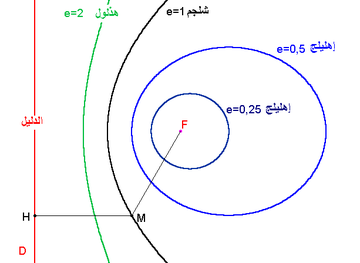
اختلاف مركزي
|
Read other articles:

Questa voce o sezione sull'argomento società calcistiche italiane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. ASD Calcio FlaminiaCalcio Rossoblù, Civitonici Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Rosso, blu Dati societari Città Civita Castellana Nazione Italia Confederazione UEFA Federazione FIGC Campionato Serie D F...

Random 1-8Album mini karya MuseDirilis4 Oktober 2000GenreRock alternatifLabelAvex TraxProduserJohn Leckie, MuseKronologi Muse Showbiz(1999)Showbiz1999 Random 1-8(2000) Origin of Symmetry(2001)Origin of Symmetry2001 Random 1-8 adalah album mini (EP) ketiga oleh band rock alternatif asal Inggris, Muse. Album ini dirilis hanya di Jepang oleh label Avex Trax pada tanggal 4 Oktober 2000[1] untuk mempromosikan tur band di sana. Album terdiri dari 6 sisi-B yang direkam selama era Showbiz...

For the neighborhood in Columbus, Georgia, see Lincoln Hills, Columbus, Georgia. Several 'knobs' in the Lincoln Hills Map of the region The Lincoln Hills extend along the Mississippi River in Missouri, starting about 40 miles (64 km) northwest of St. Louis and extending to Hannibal. They are located roughly between Highway 61 and Highway 79 in Lincoln, Pike, Ralls and Marion counties. The Lincoln Hills, locally referred to as 'knobs', may have partially escaped the most recent glaciation...

Pour les articles homonymes, voir Delmas. François Delmas Fonctions Conseiller général de l'Hérault 21 mars 1982 – 2 octobre 1988(6 ans, 6 mois et 11 jours) Élection 21 mars 1982 Réélection 17 mars 1985 Circonscription Montpellier-1 Prédécesseur Robert Noualhac Successeur Willy Diméglio 30 septembre 1973 – 25 mars 1979(5 ans, 5 mois et 23 jours) Élection 30 septembre 1973 Réélection 14 mars 1976 Circonscription Montpellier-9 Prédécesseur Créa...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Delilah gilvicornis Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Delilah Spesies: Delilah gilvicornis Delilah gilvicornis adalah spesies kumbang tanduk panjang yang tergolong famil...

Suburban tram line in Seine-Saint-Denis, north of Paris You can help expand this article with text translated from the corresponding article in French. (January 2019) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy...

SchoolLycée Français Pierre Loti d'IstanbulAddressTarabya Campus: Haydar Aliyev Caddesi n°128Beyoğlu Campus: Tomtom Kaptan Sok. BeyoğluInformationPrincipalFrédéric ColombelWebsitepierreloti.k12.tr Lycée Français Pierre Loti d'Istanbul is an international French school located in Istanbul. It was formerly known as Papillon and later took its name from the French writer Pierre Loti, who lived in Istanbul for a period of time. The school provides education from preschool to the final ye...

County in Georgia, United States County in GeorgiaMeriwether CountyCountyMeriwether County Courthouse in GreenvilleLocation within the U.S. state of GeorgiaGeorgia's location within the U.S.Coordinates: 33°02′N 84°41′W / 33.04°N 84.69°W / 33.04; -84.69Country United StatesState GeorgiaFounded1827; 197 years ago (1827)Named forDavid MeriwetherSeatGreenvilleLargest cityManchesterArea • Total505 sq mi (1,310 k...

Bucking BroadwayCuplikan filmSutradaraJohn FordProduserHarry CareyDitulis olehGeorge HivelyPemeranHarry CareyMolly MaloneSinematograferJohn W. BrownBen F. ReynoldsPerusahaanproduksiUniversal Film Manufacturing CompanyDistributorUniversal Film Manufacturing CompanyTanggal rilis24 Desember 1917Durasi53 menit (versi restorasi)NegaraAmerika SerikatBahasaBisu (intertitel Inggris) Bucking Broadway Bucking Broadway adalah sebuah film koboi bisu Amerika Serikat tahun 1917 garapan John Ford, diyakini ...

ابن الكتاني معلومات شخصية الميلاد 951قرطبة الوفاة 1029سرقسطة مواطنة الدولة الأموية في الأندلس العرق عربي الديانة الإسلام الحياة العملية المهنة طبيب تعديل مصدري - تعديل صفحة من مخطوطة «معالجة الأمراض الخطرة البادية على البدن من الخارج» في المكتبة الوطنية لع...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Fold on underside of tongue Fimbriated fold of tongueThe mouth cavity. The apex of the tongue is turned upward, and on the right side a superficial dissection of its under surface has been made. (Plica fimbriata labeled at upper right.)Prominent fringed fimbriated folds.DetailsIdentifiersLatinplica fimbriataAnatomical terminology[edit on Wikidata] The fimbriated fold of tongue, also plica fimbriata, is a slight fold of the mucous membrane on the underside of the tongue which runs laterall...

Selection of the Democratic Party nominee This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1932 Democratic Party presidential primaries – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this message) 1932 Democratic Party presidential primaries ← 1928 March 8 to...

Puerto Rican politician Herman BadilloMember of theU.S. House of Representativesfrom New YorkIn officeJanuary 3, 1971 – December 31, 1977Preceded byJacob H. GilbertSucceeded byRobert GarciaConstituency22nd district (1971–1973)21st district (1973–1977)8th Borough President of The BronxIn officeDecember 28, 1965 – December 31, 1969Preceded byJoseph F. PericoniSucceeded byRobert Abrams Personal detailsBorn(1929-08-21)August 21, 1929Caguas, Puerto RicoDiedDecember 3, 201...

North American genus of large birds This article is about all species of turkey. For its meat, see Turkey meat. For other uses, see Turkey (disambiguation) § Other common meanings. TurkeyTemporal range: 23–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N Early Miocene – Recent A male wild turkey strutting Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Galliformes Family: Phasianidae Subfamily: Phasianinae Tribe: Tetraonini Genus: Meleagris...

Upper house of the parliament of the Isle of Man Legislative Council Yn Choonceil SlattyssaghTypeTypeUpper house of the Tynwald LeadershipPresidentLaurence Skelly since 20 July 2021 StructureSeats11Political groups Independent (8) Ex officio (3)ElectionsVoting systemIndirect election by the House of KeysMeeting placeChamber of the Legislative Council, Legislative Buildings, DouglasWebsitewww.tynwald.org.im/council Politics of the Isle of Man Lord of Mann Charles III Lieutenant gov...

English historian For the anthologist, see Francis Turner Palgrave. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Francis Palgrave – news · newspapers · books · scholar · JSTOR (February 2018) (Learn how and when to remove this message) Francis PalgraveKH FRSBornJuly 1788 Died6 July 1861 (ag...

Question of whether to drill for oil in the Arctic National Wildlife Refuge ANWR and known oil deposits in northern Alaska The question of whether to drill for oil in the Arctic National Wildlife Refuge (ANWR) has been an ongoing political controversy in the United States since 1977.[1] As of 2017, Republicans have attempted to allow drilling in ANWR almost fifty times, finally being successful with the passage of the Tax Cuts and Jobs Act of 2017.[2] ANWR comprises 19 mi...

2006 film by Eytan Fox The BubbleTheatrical posterDirected byEytan FoxWritten byEytan FoxGal UchovskyProduced byRonen Ben TalStarringOhad KnollerAlon FriedmanDaniela Virtzer Yousef 'Joe' SweidShredy JabarinCinematographyYaron ScharfEdited byYosef GrunfeldYaniv RaizMusic byIvri LiderDistributed byUnited King Films [he]Release date 29 June 2006 (2006-06-29) Running time117 minutesCountryIsraelLanguagesHebrewArabicBox office$1,029,926[1] The Bubble (Hebrew: ה...

1751-52 siege of Trichinopoly during the Second Carnatic War This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2014) (Learn how and when to remove this message) Siege of TrichinopolyPart of the Second Carnatic WarMap of Trichinopoly During Second Carnatic WarDateJuly 1751 – 10 April 1752LocationTiruchirappalli, modern-day Tamil NaduResult British - ...