![]() ěąě│┘éěžěĚěžě¬ ┘ůě¬ě╣ěž┘ůě»ěę ┘äě¬┘ůěź┘Ő┘ä ěČě│┘ů ěź┘äěžěź┘Ő ěž┘äěúěĘě╣ěžě»ěî ┘ůě▒ě│┘ł┘ůěę ┘ü┘Ő ěž┘ä┘üě▒ěžě║ (ě╣┘ä┘ë ┘Ő┘ů┘Ő┘ć ěž┘äěÁ┘łě▒ěę) ┘ł┘ü┘Ő ┘ć┘üě│ ěž┘ä┘ůě│ě¬┘ł┘ë (ě╣┘ä┘ë ěž┘ä┘Őě│ěžě▒)
ěąě│┘éěžěĚěžě¬ ┘ůě¬ě╣ěž┘ůě»ěę ┘äě¬┘ůěź┘Ő┘ä ěČě│┘ů ěź┘äěžěź┘Ő ěž┘äěúěĘě╣ěžě»ěî ┘ůě▒ě│┘ł┘ůěę ┘ü┘Ő ěž┘ä┘üě▒ěžě║ (ě╣┘ä┘ë ┘Ő┘ů┘Ő┘ć ěž┘äěÁ┘łě▒ěę) ┘ł┘ü┘Ő ┘ć┘üě│ ěž┘ä┘ůě│ě¬┘ł┘ë (ě╣┘ä┘ë ěž┘ä┘Őě│ěžě▒)
ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ ┘ü┘Ő ěž┘ä┘ç┘ćě»ě│ěę ěž┘ä┘łěÁ┘ü┘Őěę ┘ç┘Ő ěĚě▒┘Ő┘éěę ě¬ě│ě¬ě╣┘ů┘ä ěąě│┘éěžěĚěžě¬ ┘ůě¬┘łěžě▓┘Őěę ┘äě¬┘ůěź┘Ő┘ä ┘ć┘ůěžě░ěČ ěź┘äěžěź┘Őěę ěž┘äěúěĘě╣ěžě». ┘łě¬ě│ě¬┘ůě» ěžě│┘ů┘çěž ┘ů┘ć ě╣ěž┘ä┘ů ěž┘äě▒┘ŐěžěÂ┘Őěžě¬ ěž┘ä┘üě▒┘ćě│┘Ő ě║ěžě│ěĘěžě▒ ┘ů┘ł┘ćěČ ěž┘äě░┘Ő ┘ŐěÁ┘ü┘çěž ┘ü┘Ő ┘âě¬ěžěĘ┘ç G├ęom├ętrie descriptive 1799.ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ ě¬ě╣ě¬┘ůě» ě╣┘ä┘ë ěž┘äěąě│┘éěžěĚěžě¬ ěž┘ä┘ůě¬ě╣ěž┘ůě»ěę ┘ä┘ä┘ć┘ů┘łě░ěČ ě╣┘ä┘ë ┘ůě│ě¬┘ł┘Ő┘Ő┘ć ┘ůě¬ě╣ěž┘ůě»┘Ő┘ć ě╣┘ä┘ë ěĘě╣ěÂ┘ç┘ůěž ěž┘äěĘě╣ěÂěî ě╣ěžě»ěę ┘ůěž ┘Ő┘â┘ł┘ć ┘łěžěşě» ┘ů┘ć┘ç┘ůěž ěú┘ü┘é┘Ő ┘łěž┘äěóě«ě▒ ě▒ěúě│┘Ő, ┘łě«ěĚ ě¬┘éěžěĚě╣┘ç┘ůěž ┘Őě│┘ů┘ë ě«ěĚ ěž┘äěúě▒ěÂ.
ěĘě╣ě» ěú┘ć ě¬ě¬┘ů ě╣┘ů┘ä┘Őěžě¬ ěž┘äěąě│┘éěžěĚ ┘ćě┤ě▒ě╣ ┘ü┘Ő ě¬ě»┘ł┘Őě▒ ěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äě▒ěúě│┘Ő ěş┘ł┘ä ě«ěĚ ěú┘äěúě▒ě ┘łěĘě╣┘âě│ ě╣┘éěžě▒ěĘ ěž┘äě│ěžě╣ěę, ┘äěČě╣┘ä┘ç ┘Őě¬ěĚěžěĘ┘é ┘ůě╣ ěž┘ä┘ůě│ě¬┘ł┘Ő ěž┘äěú┘ü┘é┘Ő. ┘çě»┘ü ┘çě░┘ç ěž┘äě╣┘ů┘ä┘Őěę ┘ç┘ł ěž┘äěşěÁ┘ł┘ä ě╣┘ä┘ë ┘ůě│ě¬┘ł┘ë ┘łěžěşě» (ěú┘ł ěĘěž┘äěžěşě▒┘ë ┘ůě│ě¬┘ł┘Ő┘Ő┘ć ┘ůě¬ěĚěžěĘ┘é┘Ő┘ć) ┘äě¬ě│┘ç┘Ő┘ä ┘éě▒ěžěíěę ┘ł┘âě¬ěžěĘěę ěž┘äě▒ě│┘ů.
ěĘěž┘äěąěÂěž┘üěę ěą┘ä┘ë ě░┘ä┘â ┘ů┘ć ěž┘ä┘ů┘ů┘â┘ć ┘łěÂě╣ ěž┘äěąě│┘éěžěĚěžě¬ ěž┘ä┘ůě¬ě╣ěž┘ůě»ěę (┘ůě│┘éěĚ ěž┘ü┘é┘Őěî ┘ł┘łěžěČ┘çěę) ┘äěú┘Ő ě┤┘â┘ä ┘ç┘ćě»ě│┘Ő ┘ü┘Ő ěşěž┘äěę ě¬┘éěžěĘ┘ä, ěú┘Ő ěž┘ć ěž┘ä┘ć┘éěžěĚ ěž┘ä┘ůě¬┘éěžěĘ┘äěę ě¬┘ćě¬┘ů┘Ő ěą┘ä┘ë ě«ěĚ┘łěĚ ě¬┘äě¬┘é┘Ő ┘ü┘Ő ┘ć┘éěĚěę ┘łěžěşě»ěę (┘ć┘çěžěŽ┘Őěę ěú┘ł ┘äěž┘ć┘çěžěŽ┘Őěę) ě¬ě│┘ů┘ë ┘ůě▒┘âě▓ ěž┘äě¬┘éěžěĘ┘ä, ┘łěž┘äě«ěĚ┘łěĚ ěž┘ä┘ůě¬┘éěžěĘ┘äěę ě¬┘äě¬┘é┘Ő ┘ü┘Ő ┘ć┘éěžěĚ ┘ůěÁěĚ┘üěę ě╣┘ä┘ë ě«ěĚ ┘łěžěşě» ┘Őě│┘ů┘ë ┘ůěş┘łě▒ ěž┘äě¬┘éěžěĘ┘ä.
┘ů┘ć ěž┘äěČě»┘Őě▒ ěĘěž┘äě░┘âě▒ ěú┘ć ěž┘äě«ěĚ┘łěĚ ěž┘äě¬┘Ő ě¬┘łěÁ┘ä ěž┘ä┘ć┘éěžěĚ ěž┘ä┘ůě¬┘éěžěĘ┘äěę ě¬ě│┘ů┘ë ě«ěĚ┘łěĚ ě¬┘ćěžěŞě▒. ěž┘äě¬┘Ő ┘Ő┘â┘ł┘ć ěžě¬ěČěž┘ç┘çěž ě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ě«ěĚ ěž┘äěúě▒ěÂ.
ě¬┘ůěź┘Ő┘ä ěž┘ä┘â┘Őěž┘ćěžě¬ ěž┘ä┘ç┘ćě»ě│┘Őěę ěž┘äě▒ěŽ┘Őě│┘Őěę
ě¬┘ůěź┘Ő┘ä ┘ć┘éěĚěę
 ě¬┘ůěź┘Ő┘ä ěž┘ä┘ć┘éěĚěę ┘ü┘Ő ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ
ě¬┘ůěź┘Ő┘ä ěž┘ä┘ć┘éěĚěę ┘ü┘Ő ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ
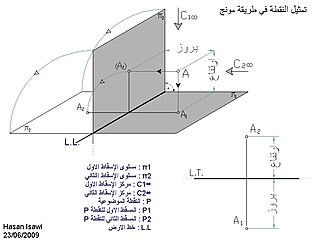
┘ü┘Ő ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ ┘ć┘éěĚěę A ┘ü┘Ő ěž┘ä┘üě▒ěžě║ ě¬┘Ć┘ůěź┘ä ě╣┘ć ěĚě▒┘Ő┘é ěąě│┘éěžěĚ┘Ő┘ć ě╣┘ů┘łě»┘Ő┘Ő┘ć ě╣┘ä┘ë ┘ůě│ě¬┘ł┘Őěžě¬ ěž┘äěąě│┘éěžěĚ:¤Ç2 ¤Ç1. ┘ć┘éěĚěę ěž┘äě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ěž┘äě«ěĚ ěž┘äě╣┘ů┘łě»┘Ő ěž┘ä┘ůěžě▒ ěĘěž┘ä┘ć┘éěĚěę A ┘łěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äěú┘ü┘é┘Ő ¤Ç1, ┘ç┘Ő ěž┘ä┘ůě│┘éěĚ ěž┘äěú┘ł┘ä (ěú┘ł ěž┘äěú┘ü┘é┘Ő) ┘ä┘ä┘ć┘éěĚěę A ┘ł┘Ő┘Ćě▒┘ůě▓ ┘ä┘çěž A1. ěĘěĚě▒┘Ő┘éěę ┘ů┘ůěžěź┘äěę ┘Őěşě»ě» ěž┘ä┘ůě│┘éěĚ ěž┘äěźěž┘ć┘Ő A2 ┘â┘ć┘éěĚěę ě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ¤Ç2 (┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő) ┘łěž┘äě«ěĚ ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç2 ┘łěž┘ä┘ůěžě▒ ěĘěž┘ä┘ć┘éěĚěę A.
- ěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äěú┘ü┘é┘Ő ¤Ç1: ┘Őě│┘ů┘ë ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ł┘ä
- ěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äě▒ěžě│┘Ő ¤Ç2: ┘Őě│┘ů┘ë ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő
- ěú┘äěžě¬ěČěž┘ç ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç1 ┘Őě│┘ů┘ë ┘ůě▒┘âě▓ ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ł┘ä
- ěú┘äěžě¬ěČěž┘ç ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç2 ┘Őě│┘ů┘ë ┘ůě▒┘âě▓ ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő
- ěž┘äě«ěĚ ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç1, ┘Őě│┘ů┘ë ě«ěĚ ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ł┘ä
- ěž┘äě«ěĚ ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç2, ┘Őě│┘ů┘ë ě«ěĚ ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő
- ěžě▒ě¬┘üěžě╣ A: ┘ůě│ěž┘üěę (ěú┘ł ěĘ┘Ćě╣ě») ěž┘ä┘ć┘éěĚěę A ě╣┘ć ¤Ç1
- ěĘě▒┘łě▓ A: ┘ůě│ěž┘üěę ěž┘ä┘ć┘éěĚěę A ě╣┘ć ¤Ç2
┘ůěźěž┘ä
┘ä┘ćě╣┘Ő┘ć ┘ć┘éěĚěę P ┘ü┘Ő ěž┘äě▓ěž┘ł┘Őěę ěž┘äě▓┘łěČ┘Őěę ěž┘äěú┘ł┘ä┘ë (I diedro), ┘üě╣┘ů┘ä┘Őěę ě¬ěşě»┘Őě» ěž┘äěąě│┘éěžěĚěžě¬ ěž┘ä┘ů┘ł┘ćěČ┘Őěę ┘ä┘ä┘ć┘éěĚěę P ě¬ě¬┘ů ┘â┘ůěž ┘Ő┘ä┘Ő:
- ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ł┘ä P1 ┘ä┘ä┘ć┘éěĚěę P, ┘Őěşě»ě» ┘â┘ć┘éěĚ┘ç ě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ěž┘äě«ěĚ ěž┘äě▒ěúě│┘Ő ěž┘ä┘ůěžě▒ ěĘěž┘ä┘ć┘éěĚěę P ┘łěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äěú┘ł┘ä ¤Ç1 (┘Őě│┘ů┘ë ěú┘ŐěÂěž┘ő ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěž┘ü┘é┘Ő).
- ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő P2 ┘ä┘ä┘ć┘éěĚěę P, ┘Őěşě»ě» ┘â┘ć┘éěĚ┘ç ě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő ¤Ç2 (┘Őě│┘ů┘ë ěú┘ŐěÂěž┘ő ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěž┘ůěž┘ů┘Ő) ┘łěž┘äě«ěĚ ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç2 (┘Őě│┘ů┘ë ě«ěĚ ěž┘äěąě│┘éěžěĚ┘Ő ěž┘äěźěž┘ć┘Ő).
ěž┘ä┘ůě│ě¬┘ł┘ë ěž┘ä┘ůěžě▒ ěĘěž┘ä┘ć┘éěĚěę P ┘łěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ěž┘ä┘ůě│ě¬┘ł┘Ő┘Ő┘ć ¤Ç1 ┘ł¤Ç2, ┘Ő┘éěĚě╣┘ç┘ůěž ěĘě«ěĚ┘Ő┘ć ě╣┘ů┘łě»┘Ő┘Ő┘ć ě╣┘ä┘ë ě«ěĚ ěž┘äěúě▒ěÂ. ┘ć┘éěĚěę ě¬┘éěžěĚě╣ ┘çě░ěž ěž┘ä┘ůě│ě¬┘ł┘ë ┘ůě╣ ě«ěĚ ěž┘äěúě▒ě ě¬ě│┘ů┘ë ěž┘ä┘ć┘éěĚěę ěž┘ä┘ůě▒ěČě╣┘Őěę ┘ł┘Őě▒┘ůě▓ ┘ä┘çěž P0 (ěĘ┘Ő ě▓┘Őě▒┘ł). ┘łěĘ┘çě░ěž:
- ěžě▒ě¬┘üěžě╣ P = ěž┘ä┘ůě│┘é┘Ő┘ů P_P1 ěž┘äě░┘Ő ┘Őě│ěž┘ł┘Ő ěú┘ŐěÂěž┘ő P2_P0
- ěĘě▒┘łě▓ P = ěž┘ä┘ůě│┘é┘Ő┘ů P_P2 ěž┘äě░┘Ő ┘Őě│ěž┘ł┘Ő ěú┘ŐěÂěž┘ő P1_P0
ě¬┘ůěź┘Ő┘ä ě«ěĚ
 ě¬┘ůěź┘Ő┘ä ┘ů┘ł┘ćěČ┘Ő ┘äě«ěĚ ě╣ěž┘ů
ě¬┘ůěź┘Ő┘ä ┘ů┘ł┘ćěČ┘Ő ┘äě«ěĚ ě╣ěž┘ů
┘Őě¬┘ů ě¬ěşě»┘Őě» ěž┘äěąě│┘éěžěĚěžě¬ ěž┘ä┘ůě¬ě╣ěž┘ůě»ěę r1 r2 ┘äě«ěĚ r ┘ů┘łěÂ┘łě╣ ┘ü┘Ő ěž┘ä┘üě▒ěžě║, ┘â┘ůěž ┘Ő┘ä┘Ő:
- ěž┘äěąě│┘éěžěĚ ěú┘äěž┘ü┘é┘Ő r1 ┘ä┘äě«ěĚ r ┘âě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ü┘é┘Ő ¤Ç1 ┘łěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äě▒ěžě│┘Ő ěž┘ä┘ůěžě▒ ěĘěž┘äě«ěĚ r.
- ┘łěĘěž┘ä┘ůěź┘ä ěž┘äěąě│┘éěžěĚ ěž┘äě▒ěžě│┘Ő r2ěî ┘Őěşě»ě» ┘âě«ěĚ ě¬┘éěžěĚě╣ ěĘ┘Ő┘ć ┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äě▒ěžě│┘Ő ¤Ç2 ┘łěž┘ä┘ůě│ě¬┘ł┘ë ěž┘äě╣┘ů┘łě»┘Ő ě╣┘ä┘ë ¤Ç2 ┘łěž┘ä┘ůěžě▒ ěĘěž┘äě«ěĚ r.
ě╣┘ů┘ä┘Őěž┘őěî ┘äě¬ěşě»┘Őě» ěž┘äěąě│┘éěžěĚěžě¬ ěž┘ä┘ů┘ł┘ćěČ┘Őěę (r1 r2)ěî ┘äě«ěĚ r ,ě╣┘ä┘ë ě│ěĘ┘Ő┘ä ěž┘ä┘ůěźěž┘ä r1ěî ┘ů┘ć ěž┘äěÂě▒┘łě▒┘Ő ě¬ěşě»┘Őě» ěąě│┘éěžěĚ┘Ő┘ć (P1 Q1) ┘ä┘ć┘éěĚě¬┘Ő┘ć (P Q) ┘Ő┘ćě¬┘ů┘Őěž┘ć ┘ä┘äě«ěĚ r. ┘ł┘äěú┘ć ěž┘äě«ěĚ r ┘ćěŞě▒┘Őěž ┘Őě╣ě¬ěĘě▒ ┘â┘Őěž┘ć ě║┘Őě▒ ┘ůěşě»┘łě»ěęěî ┘üěž┘ä┘ć┘éěĚě¬┘Ő┘ć ┘Ő┘ů┘â┘ć ěú┘ć ┘Ő┘â┘ł┘ćěž┘ć ěóěźěžě▒ ě░┘ä┘â ěž┘äě«ěĚ rěî ěú┘Ő ┘ć┘éěžěĚ ěž┘äě¬┘éěžěĚě╣ (T'r T"r) ěĘ┘Ő┘ć ěž┘äě«ěĚ r ┘ł┘ůě│ě¬┘ł┘Ő┘Ő ěž┘äěąě│┘éěžěĚ (¤Ç2 ¤Ç1).
- ┘ć┘éěĚěę ěž┘äě¬┘éěžěĚě╣ T'r ěĘ┘Ő┘ć ě«ěĚ r ┘ł┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äěú┘ü┘é┘Ő ¤Ç1ěî ě¬ě│┘ů┘ë ěž┘äěúěźě▒ ěž┘äěú┘ł┘ä ┘ä┘äě«ěĚ r.
- ěú┘ůěž ┘ć┘éěĚěę ěž┘äě¬┘éěžěĚě╣ T"r ěĘ┘Ő┘ć ě«ěĚ r ┘ł┘ůě│ě¬┘ł┘ë ěž┘äěąě│┘éěžěĚ ěž┘äě▒ěúě│┘Ő ¤Ç2ěî ě¬ě│┘ů┘ë ěž┘äěúěźě▒ ěž┘äěźěž┘ć┘Ő ┘ä┘äě«ěĚ r.
ě¬┘ůěź┘Ő┘ä ┘ůě│ě¬┘ł┘ë
 ┘ůě│ě¬┘ł┘Ő┘Ő ěž┘äěžě│┘éěžěĚ ┘ü┘Ő ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ
┘ůě│ě¬┘ł┘Ő┘Ő ěž┘äěžě│┘éěžěĚ ┘ü┘Ő ěĚě▒┘Ő┘éěę ┘ů┘ł┘ćěČ
ěž┘ä┘ůě│ě¬┘ł┘ë ┘ů┘ć ěž┘ä┘ćěžěş┘Őěę ěž┘ä┘ćěŞě▒┘Őěę ┘Őě╣ě¬ěĘě▒ ┘äěž┘ć┘çěžěŽ┘Ő, ┘łěĘěž┘äě¬ěž┘ä┘Ő ěž┘äěĚě▒┘Ő┘éěę ěž┘ä┘łěş┘Őě»ěę ┘äě¬┘ůěź┘Ő┘ä┘ç ┘Őě¬┘ů ┘ů┘ć ě«┘äěž┘ä ě«ěĚ┘łěĚ ě¬┘éěžěĚě╣┘ç ┘ůě╣ ┘ůě│ě¬┘ł┘Őěžě¬ ěž┘äěžě│┘éěžěĚ. ┘ł┘çě░┘ç ěž┘äě«ěĚ┘łěĚ ě¬ě│┘ů┘ë ěžěźěžě▒ ěž┘ä┘ůě│ě¬┘ł┘ë. ┘ůěź┘äěž ě¬┘éěžěĚě╣ ┘ůě│ě¬┘ł┘ë ěž┘ä┘üěž ┘ůě╣ ┘ůě│ě¬┘ł┘ë ěž┘äěžě│┘éěžěĚ ěž┘äěú┘ł┘ä ┘Őě│┘ů┘ë ěž┘äěžěźě▒ ěž┘äěú┘ł┘ä ┘ä┘ä┘ůě│ě¬┘ł┘ë ěž┘ä┘üěž, ┘łě«ěĚ ě¬┘éěžěĚě╣ ěž┘ä┘üěž ┘ůě╣ ┘ůě│ě¬┘ł┘ë ěž┘äěžě│┘éěžěĚ ěž┘äěźěž┘ć┘Ő ┘Őě│┘ů┘ë ěž┘äěžěźě▒ ěž┘äěźěž┘ć┘Ő ┘ä┘ä┘ůě│ě¬┘ł┘ë ěž┘ä┘üěž.
ě¬ěžě▒┘Őě«
┘ů┘ł┘ćěČ ě¬ě╣┘çě» ěĘě╣ě»┘ů ěž┘ä┘âě┤┘ü ě╣┘ć ěž┘äěĚě▒┘Ő┘éěę ěž┘ä┘ů┘łěÁ┘ł┘üěę ěúě╣┘äěž┘çěî ěž┘äě¬┘Ő ┘âěž┘ćě¬ ě│ě▒ ě╣ě│┘âě▒┘Ő ┘ä┘ůě»┘ç 15 ě╣ěž┘ůěž. ┘ü┘éěĚ ┘ü┘Ő 1794ěî ě│┘ůěş ěĘě¬ě»ě▒┘Őě│┘çěž ┘ü┘Ő ěĘěžě▒┘Őě│.
[1]
ěĘěĘ┘ä┘Ő┘łě║ě▒ěž┘ü┘Őěž
┘ůě╣ě▒ě ěÁ┘łě▒
┘ůěÁěžě»ě▒
┘łěÁ┘äěžě¬ ě«ěžě▒ěČ┘Őěę