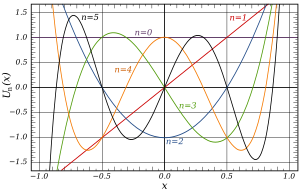
متعددات الحدود لتشيبيشيف
|
Read other articles:

Lily FrankyLily Franky di acara pembukaan Tokyo International Film Festival, 2017.LahirMasaya Nakagawa4 November 1963 (umur 60)Fukuoka, JepangNama lainElvis WoodstockPekerjaanAktor, penulis, ilustrator, desainer, musikus, penulis lagu, fotografer, kritikusTahun aktif1980-an–sekarangTinggi174 cm (5 ft 9 in) Lily Franky (リリー・フランキーcode: ja is deprecated , rirī furankī, nama lahir: Masaya Nakagawa (中川 雅也code: ja is deprecated , Nakagawa...

Matius 16Potongan naskah Papirus Magdalen berisi Injil Matius, yang ditulis sekitar tahun 50-70 M.KitabInjil MatiusKategoriInjilBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen1← pasal 15 pasal 17 → Matius 16 (disingkat Mat 16) adalah pasal keenam belas Injil Matius pada Perjanjian Baru dalam Alkitab Kristen, yang diyakini disusun menurut catatan Matius, salah seorang dari Keduabelas Rasul Yesus Kristus.[1][2][3][4] Teks Naskah aslinya...

Jeremy SistoJeremy Sisto dalam film Into Temptation tahun 2008LahirJeremy Merton Sisto6 Oktober 1974 (umur 49)[1]Grass Valley, California, Amerika SerikatTempat tinggalLaurel Canyon, Los Angeles, California, Amerika SerikatAlmamaterUCLAPekerjaan Aktor produser penulis Tahun aktif1991–sekarangSuami/istri Marisa Ryan (m. 1993; bercerai 2002) Addie Lane (m. 2009) Anak2 Jeremy Merton Sisto (lah...

Czech RepublicKaptenJaroslav NavrátilPeringkat ITFPeringkat terkini2Penampilan pertama1921World GroupPenampilan28 (21-27)Hasil terbaik1 (1980)Runner-up2 (1975, 2009)Statistik pemainKemenangan terbanyakJan Kodeš (60-34)Menang terbanyak – TunggalRoderich Menzel (40-12)Menang terbanyak – GandaJan Kodeš (21-15)Tim ganda terbaikJaroslav Drobný dan Vladimír Černík (11-2)Bermain terbanyakJan Kodeš (39)Penampilan terbanyakJan Kodeš (15) Tim PIala Davis Republik Ceko adalah tim yang mewak...

James Tavernier Tavernier con la maglia dei Rangers nel 2018 Nazionalità Inghilterra Altezza 175 cm Peso 75 kg Calcio Ruolo Difensore, centrocampista Squadra Rangers Carriera Giovanili 2000-2007 Leeds Utd2007-2009 Newcastle Utd Squadre di club1 2009-2010 Newcastle Utd0 (0)2010-2011→ Gateshead13 (0)2011→ Carlisle Utd16 (0)2011-2012→ Sheffield Wednesday6 (0)2012→ MK Dons7 (0)2012-2013 Newcastle Utd2 (0)2013→ Shrewsbury To...

American politician This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Edwin Hallowell – news · newspapers · books · scholar · JSTOR (June 2007) (Learn how and when to remove this template message) Edwin HallowellMember of the U.S. House of Representativesfrom Pennsylvania's 7th districtIn officeMar...

Chemical element, symbol W and atomic number 74 This article is about the chemical element. For other uses, see Tungsten (disambiguation). Chemical element, symbol W and atomic number 74Tungsten, 74WTungstenPronunciation/ˈtʌŋstən/ (TUNG-stən)Alternative namewolfram, pronounced: /ˈwʊlfrəm/ (WUUL-frəm)Allotropesα-tungsten (common), β-tungstenAppearancegrayish white, lustrousStandard atomic weight Ar°(W)183.84±0.01[1]183.84±0.01 (abridged) ...

Keuskupan Massa Marittima-PiombinoDioecesis Massana-PlumbinensisKatolik Katedral Massa MarittimaLokasiNegaraItaliaProvinsi gerejawiSiena-Colle di Val d'Elsa-MontalcinoStatistikLuas1.200 km2 (460 sq mi)Populasi- Total- Katolik(per 2004)127.677126,000 (98.7%)Paroki53InformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-5KatedralBasilica Cattedrale di Cerbone Vescovo (Massa Marittima)KonkatedralChiesa Abbaziale di S. Antimo Martire (Piombino)Kepemimp...

Spanish Viceroy (1767–1822) In this Spanish name, the first or paternal surname is de Elío and the second or maternal family name is Olóndriz. The Most ExcellentThe Marquess of VesollaPortrait by Miguel Parra, ca. 1815Viceroy of the Río de la Plata Personal detailsBorn5 March 1767Pamplona, SpainDied4 September 1822(1822-09-04) (aged 55)Valencia, Spain Francisco Javier de Elío y Olóndriz (1767 – 1822) was a Spanish soldier and governor of Montevideo. He was instrument...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2015年7月23日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目內容疑欠准确,有待查證。 (2015年7月23日)請在讨论页討論問題所在及加以改善,若此條目仍有爭議及准确度欠佳,會被提出存廢討論。 此條目之中立性有�...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Administrative entry restrictions A Chilean passport A Chilean identity card is valid for travel to most South American countries Visa requirements for Chilean citizens are administrative entry restrictions by the authorities of other states placed on citizens of Chile entering with a Chilean passport. As of 2024, Chilean citizens had visa-free or visa on arrival access to 177 countries and territories, ranking the Chilean passport 16th in the world according to the Henley Passport Index.[...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Family of fish For other uses, see Stickleback (disambiguation). Sticklebacks Four marine species of stickleback from the Atlantic Ocean coast of North America Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Scorpaeniformes Suborder: Gasterosteoidei Family: GasterosteidaeBonaparte, 1831[1] Genera see text The sticklebacks are a family of ray-finned fishes, the Gasterosteidae which have a Holarctic distribution in fresh, brack...

Ilustrasi Sapi Cacar Sapi adalah penyakit cacar yang disebabkan oleh virus variola.[1] Penyebab cacar ini adalah anggota dari genus orthopoxvirus, yang juga termasuk virus seperti cacar sapi, cacar monyet, dan kontagiosum moluskum.[2] Sejarah Pada bulan Mei 1796, untuk pertama kalinya dilakukan imunisasi pada pasien cacar air dengan material dari luka cacar air sapi.[3] Edward Jenner menyuntik James Phipps, seorang bocah lelaki berumur delapan tahun dengan sesuatu yang...

Pour les articles homonymes, voir Languedoc (homonymie). Pour l’article ayant un titre homophone, voir Langue d'oc. Languedoc(oc) Lengadòc Gouvernement de LanguedocIntendance de Languedoc 1271 – 1790 Gouvernement militaire du Languedoc dans le royaume de France en 1789.Informations générales Statut Province (gouvernement et intendance) du royaume de France : pays d'états, de taille réelle, de petite gabelle et, en matière de traites, réputé étranger. Capitale...

Main article: 2012 United States presidential election 2012 United States presidential election in Colorado ← 2008 November 6, 2012 2016 → Turnout71.17% [1] Nominee Barack Obama Mitt Romney Party Democratic Republican Home state Illinois Massachusetts Running mate Joe Biden Paul Ryan Electoral vote 9 0 Popular vote 1,323,102 1,185,243 Percentage 51.45% 46.09% County Results Obama 40-50% 50-60% 60-70%...

American musician (1941–2010) Captain BeefheartBeefheart performing at Convocation Hall in 1974Background informationBirth nameDon Glen VlietAlso known as Bloodshot Rollin' Red Don Van Vliet Born(1941-01-15)January 15, 1941Glendale, California, U.S.DiedDecember 17, 2010(2010-12-17) (aged 69)Arcata, California, U.S.[1]GenresBlues rockavant-rockOccupation(s)Singer-songwritermusicianpainterpoetcomposerauthorrecord producerfilm directorInstrument(s)Vocalsharmonicasaxophoneclarineto...

2011 New York's 9th congressional district special election ← 2010 September 13, 2011 2012 → New York's 9th congressional district Nominee Bob Turner David Weprin Party Republican Democratic Alliance Conservative Parties Working Families Independence Popular vote 37,342 33,656 Percentage 51.7% 46.6% County resultsTurner: 60–70%Weprin: 50–60% U.S. Representative before election Anthony Weiner Dem...
























![{\displaystyle T_{n}(x)={\begin{cases}\cos(n\arccos(x)),&\ x\in [-1,1]\\\cosh(n\,\mathrm {arccosh} (x)),&\ x\geq 1\\(-1)^{n}\cosh(n\,\mathrm {arccosh} (-x)),&\ x\leq -1\\\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e04cd2a79ed30188c173e0d47a7a69846d8366)