![]() ž¬ž▒ž¦┘āž© ┘ģ┘łž¼ž¦ž¬ ┘ģž│ž¬┘ł┘Ŗž® (ž╣ž▒žČ┘Ŗž®) ┘ł┘ģ┘łž¼ž¦ž¬ ┘垦ž┤ž”ž® ž╣┘å žŁž▒┘āž® ž¦┘äž©žĘ ┘ü┘Ŗ ž¦┘ä┘ģž¦žĪ.
ž¬ž▒ž¦┘āž© ┘ģ┘łž¼ž¦ž¬ ┘ģž│ž¬┘ł┘Ŗž® (ž╣ž▒žČ┘Ŗž®) ┘ł┘ģ┘łž¼ž¦ž¬ ┘垦ž┤ž”ž® ž╣┘å žŁž▒┘āž® ž¦┘äž©žĘ ┘ü┘Ŗ ž¦┘ä┘ģž¦žĪ.
┘ģž©ž»žŻ ž¦┘䞬ž▒ž¦┘āž© ┘ü┘Ŗ ž¦┘ä┘ü┘Ŗž▓┘Ŗž¦žĪ ┘Ŗ┘åžĄ ž╣┘ä┘ē žŻ┘å┘ć ┘ü┘Ŗ ž¼┘ģ┘Ŗž╣ ž¦┘䞯┘åžĖ┘ģž® ž¦┘äž«žĘ┘Ŗž® ž¬┘ā┘ł┘å ┘ģžŁžĄ┘äž® ž¬žŻž½┘Ŗž▒┘Ŗ┘å žŻ┘ł žŻ┘āž½ž▒ ž╣ž©ž¦ž▒ž® ž╣┘å ┘ģž¼┘ģ┘łž╣ ž¦┘䞬žŻž½┘Ŗž▒┘Ŗ┘å.[1][2] ┘üžźž░ž¦ ┘āž¦┘å ž¦┘䞬žŻž½┘Ŗž▒ A ┘Ŗ┘Å┘垬ž¼ ž¦┘ä┘垦ž¬ž¼ X ┘łž¦┘䞬žŻž½┘Ŗž▒ B ┘Ŗ┘Å┘垬ž¼ ž¦┘ä┘垦ž¬ž¼ Y ┘üžź┘å ž¦┘䞬žŻž½┘Ŗž▒┘Ŗ┘å (A + B) ┘Ŗ┘垬ž¼ž¦┘å ž¦┘ä┘垦ž¬ž¼ (X + Y).
ž¦┘䞬ž▒ž¦┘āž© ┘ć┘ł žŻžŁž» ž¦┘äž┤ž▒┘łžĘ ž¦┘äžČž▒┘łž▒┘Ŗž® ┘䞦ž╣ž¬ž©ž¦ž▒ ž»ž¦┘äž® ┘ģž¦ ┬½ž»ž¦┘äž® ž«žĘ┘Ŗž®┬╗. ┘ł┘ģ┘å ž«┘łž¦žĄ ž¦┘äž»ž¦┘äž® ž¦┘äž«žĘ┘Ŗž® žŻ┘å┘枦 ž¬┘ü┘Ŗ ž©ž«ž¦žĄ┘Ŗž® ž¦┘䞬ž▒ž¦┘āž© ž©ž¦┘äž¼┘ģž╣žī ┘łžŻ┘å ž¬┘ā┘ł┘å žŻ┘ŖžČž¦ ┘ģž¬ž¼ž¦┘åž│ž® ┘ģ┘å ž¦┘äž»ž▒ž¼ž® ž¦┘䞯┘ł┘ä┘ē (┘Ŗž¼ž▒┘Ŗ ž╣┘ä┘Ŗ┘枦 ž¦┘äžČž▒ž© ž¦┘ä┘ģž╣ž¬ž¦ž» scalar multiplication ┘łž¬ž╣ž▒┘ü ž©ž¦┘ä┘ģž╣ž¦ž»┘äž®:
 (ž¬ž▒ž¦┘āž©)
(ž¬ž▒ž¦┘āž©)
┘ŖžĘž©┘é ┘ģž©ž»žŻ ž¦┘䞬ž▒ž¦┘āž© ┘ü┘Ŗ ž¦┘ä┘ģ┘łž¼ž¦ž¬ ž¦┘ä┘ā┘ćž▒┘ł┘ģž║┘垦žĘ┘Ŗž│┘Ŗž® ┘ł┘ü┘Ŗ ž¦┘äž©žĄž▒┘Ŗž¦ž¬ ┘ł┘ü┘Ŗ ž¬┘é┘å┘Ŗž® ž¦┘䞦ž¬žĄž¦┘䞦ž¬ ┘ł┘ü┘Ŗ ž¼┘ģž╣ ž¦┘ä┘é┘ł┘ē ┘ü┘Ŗ ž¦┘ä┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘䞦ž│┘Ŗ┘ā┘Ŗž® ┘ł┘ü┘Ŗ ž¦┘䞣ž¦┘䞦ž¬ ž¦┘ä┘ā┘ģ┘ł┘ģ┘Ŗž® ┘ü┘Ŗ ┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘ģ.
ž▒┘Ŗž¦žČ┘Ŗž¦
┘Ŗ┘ģ┘ā┘å ž¬┘ģž½┘Ŗ┘ä ž¦┘䞬ž▒ž¦┘āž© ž©ž»ž¦┘äž® ž«žĘ┘Ŗž®:

žŁ┘Ŗž½ ┘Ŗž╣┘å┘Ŗ ž¦┘äž¼┘ģž╣ žŻ┘å ž»ž¦┘䞦ž¬ žŻ┘ł ┘ā┘ģ┘Ŗž¦ž¬  ┘ģ┘å ┘å┘üž│ ž¦┘ä┘å┘łž╣ ┘Ŗ┘ģ┘ā┘å ž¼┘ģž╣┘枦 ┘䞬┘ā┘ł┘Ŗ┘å ┘ā┘ģ┘Ŗž® ž¼ž»┘Ŗž»ž®
┘ģ┘å ┘å┘üž│ ž¦┘ä┘å┘łž╣ ┘Ŗ┘ģ┘ā┘å ž¼┘ģž╣┘枦 ┘䞬┘ā┘ł┘Ŗ┘å ┘ā┘ģ┘Ŗž® ž¼ž»┘Ŗž»ž®  . ┘ł┘Ŗž╣žĘ┘Ŗ ž¦┘ä┘ģž╣ž¦┘ģ┘ä
. ┘ł┘Ŗž╣žĘ┘Ŗ ž¦┘ä┘ģž╣ž¦┘ģ┘ä  ┘åž│ž©ž® (ž¬žŻž½┘Ŗž▒) ┘ā┘ä ┘ģ┘å ž¦┘ä┘ā┘ģ┘Ŗž¦ž¬ ž¦┘ä┘ģ┘ā┘ł┘åž® ┘ä┘枦.
┘åž│ž©ž® (ž¬žŻž½┘Ŗž▒) ┘ā┘ä ┘ģ┘å ž¦┘ä┘ā┘ģ┘Ŗž¦ž¬ ž¦┘ä┘ģ┘ā┘ł┘åž® ┘ä┘枦.
┘Ŗ┘åžĘž©┘é ┘ģž©ž»žŻ ž¦┘䞬ž▒ž¦┘āž© ž╣┘ä┘ē ┘āž½┘Ŗž▒ ┘ģ┘å ž¦┘䞯┘åžĖ┘ģž®žī ┘łž╣┘ä┘ē ž¦┘ä┘ģž╣ž¦ž»┘䞦ž¬ ž¦┘䞬┘üž¦žČ┘ä┘Ŗž® ž¦┘äž«žĘ┘Ŗž®. ┘üžźž░ž¦ ┘āž¦┘å ┘ä┘ģž╣ž¦ž»┘äž® ž¬┘üž¦žČ┘ä┘Ŗž® ž«žĘ┘Ŗž® žŁ┘䞦┘å  ┘ł
┘ł ┘ü┘Ŗž┤┘ā┘ä ┘ģž¼┘ģ┘łž╣┘ć┘ģž¦ žŻ┘ŖžČž¦ žŁ┘䞦žī žŻ┘Ŗ žŻ┘å
┘ü┘Ŗž┤┘ā┘ä ┘ģž¼┘ģ┘łž╣┘ć┘ģž¦ žŻ┘ŖžČž¦ žŁ┘䞦žī žŻ┘Ŗ žŻ┘å  žŁ┘䞦 ┘ä┘ä┘ģž╣ž¦ž»┘äž®.
žŁ┘䞦 ┘ä┘ä┘ģž╣ž¦ž»┘äž®.
┘łž©žĄ┘üž® ž╣ž¦┘ģž®:
- "žźž░ž¦ ┘āž¦┘垬
 žŁž¬┘ē
žŁž¬┘ē  žŁ┘ä┘ł┘䞦 ┘ä┘ģž╣ž¦ž»┘äž® ž¬┘üž¦žČ┘ä┘Ŗž® ž«žĘ┘Ŗž®žī ┘ü┘Ŗ┘ā┘ł┘å ┘ā┘ä ┘ģž¼┘ģ┘łž╣ ┘ćž░┘ć ž¦┘䞣┘ä┘ł┘ä žŻ┘ŖžČž¦ žŁ┘䞦 ┘ä┘ä┘ģž╣ž¦ž»┘äž® ž¦┘䞬┘üž¦žČ┘ä┘Ŗž®."
žŁ┘ä┘ł┘䞦 ┘ä┘ģž╣ž¦ž»┘äž® ž¬┘üž¦žČ┘ä┘Ŗž® ž«žĘ┘Ŗž®žī ┘ü┘Ŗ┘ā┘ł┘å ┘ā┘ä ┘ģž¼┘ģ┘łž╣ ┘ćž░┘ć ž¦┘䞣┘ä┘ł┘ä žŻ┘ŖžČž¦ žŁ┘䞦 ┘ä┘ä┘ģž╣ž¦ž»┘äž® ž¦┘䞬┘üž¦žČ┘ä┘Ŗž®."
ž¬ž»ž¦ž«┘ä ž¦┘ä┘ģ┘łž¼ž¦ž¬
combined
waveform
|

|
| wave 1
|
| wave 2
|
|
┘ģ┘łž¼ž¬ž¦┘å ž©┘üž▒┘é žĘ┘łž▒ 180┬░
|
┘ģ┘łž¼ž¬ž¦┘å ┘ü┘Ŗ ┘å┘üž│ ž¦┘äžĘ┘łž▒
|
┘Ŗž╣┘å┘Ŗ ž¦┘䞬ž▒ž¦┘āž© ┘ü┘Ŗ ž╣┘ä┘ģ ž¦┘ä┘ģ┘łž¼ž¦ž¬ ž¬ž»ž¦ž«┘ä ┘ģ┘łž¼ž¦ž¬ ┘ä┘枦 ┘å┘üž│ žĘ┘ł┘ä ž¦┘ä┘ģ┘łž¼ž®. ┘łž¬ž¬ž║┘Ŗž▒ ┘ü┘Ŗ ┘ćž░┘ć ž¦┘䞣ž¦┘äž® ┘é┘Ŗ┘ģž® ┘ģžĘž¦┘ä ž¦┘ä┘ģ┘łž¼ž® ž¦┘ä┘垦ž¬ž¼ž®. ┘üž╣┘ä┘ē ž│ž©┘Ŗ┘ä ž¦┘ä┘ģž½ž¦┘ä ž╣┘åž» ž¬ž»ž¦ž«┘ä ž╣ž»ž® žŻ┘ģ┘łž¦ž¼ ┘ģž¦ž”┘Ŗž® žŻ┘ł ž╣ž»ž® žŻ┘ģ┘łž¦ž¼ ┘ā┘ćž▒┘ł┘ģž║┘垦žĘ┘Ŗž│┘Ŗž® ┘üžź┘ģž¦ žŻ┘å ž¬┘é┘ł┘ē ž©ž╣žČ┘枦 žŻ┘ł ž¬žČž╣┘ü ┘ģžŁžĄ┘䞬┘枦.
 ž¬ž»ž¦ž«┘ä ┘ģ┘łž¼ž¬┘Ŗ┘å.
ž¬ž»ž¦ž«┘ä ┘ģ┘łž¼ž¬┘Ŗ┘å.
ž¬ž¬žĄ┘ü ž¦┘äž»ž¦┘äž® ž¦┘ä┘ģ┘łž¼┘Ŗž® ž¦┘ä┘垦ž¬ž¼ž®  ž©ž¦┘äž«ž¦žĄ┘Ŗž®:
ž©ž¦┘äž«ž¦žĄ┘Ŗž®:

žŁ┘Ŗž½:
 ž¦┘äž»┘łž¦┘ä ž¦┘ä┘ģ┘łž¼┘Ŗž® ┘ä┘ä┘ģ┘łž¼ž¦ž¬ ž¦┘䞯žĄ┘ä┘Ŗž®.
ž¦┘äž»┘łž¦┘ä ž¦┘ä┘ģ┘łž¼┘Ŗž® ┘ä┘ä┘ģ┘łž¼ž¦ž¬ ž¦┘䞯žĄ┘ä┘Ŗž®.
┘ü┘Ŗ ž¦┘ä┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘䞦ž│┘Ŗ┘ā┘Ŗž®
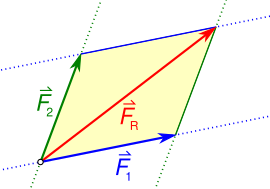 ┘ģž¬┘łž¦ž▓┘Ŗ žŻžČ┘䞦ž╣ ž¦┘ä┘é┘ł┘ē: ž¦┘äž│┘ć┘ģ ž¦┘䞯žŁ┘ģž▒ ┘ć┘ł ┘ģžŁžĄ┘äž® ž¦┘ä┘é┘łž¬┘Ŗ┘å F1 ┘ł F2.
┘ģž¬┘łž¦ž▓┘Ŗ žŻžČ┘䞦ž╣ ž¦┘ä┘é┘ł┘ē: ž¦┘äž│┘ć┘ģ ž¦┘䞯žŁ┘ģž▒ ┘ć┘ł ┘ģžŁžĄ┘äž® ž¦┘ä┘é┘łž¬┘Ŗ┘å F1 ┘ł F2.
ž¬ž¬ž▒ž¦┘āž© žŻ┘ŖžČž¦ ž¦┘ä┘é┘ł┘ē ž¦┘ä┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘ā┘Ŗž®. ┘łž¬ž│┘ģ┘ē ┘ćž░┘ć ž¦┘äž«ž¦žĄ┘Ŗž® žŻžŁ┘Ŗž¦┘垦 ┬½ž¦┘ä┘鞦┘å┘ł┘å ž¦┘äž▒ž¦ž©ž╣ ┘ä┘å┘Ŗ┘łž¬┘å┬╗.
žĄ┘Ŗž║ž¬┘枦 ž¦┘äž▒┘Ŗž¦žČ┘Ŗž® ┘āž¦┘äžóž¬┘Ŗ:

┘ćž░┘ć ž¦┘ä┘ģž╣ž¦ž»┘äž® ž¬┘é┘ł┘ä žŻ┘å ž¦┘ä┘é┘ł┘ē ž¦┘ä┘ģž«ž¬┘ä┘üž® ž¦┘äž╣ž¦┘ģ┘äž® ž╣┘ä┘ē žŻžŁž» ž¦┘䞯ž¼ž│ž¦┘ģ ┘Ŗ┘ģ┘ā┘å ž¦ž«ž¬žĄž▒┘枦 ┘ü┘Ŗ ┬½┘ģžŁžĄ┘äž®┬╗ ž¬┘é┘ł┘ģ ┘ģ┘鞦┘ģ┘ć┘ģ.
┘ģž½ž¦┘ä ž╣┘ä┘ē ž░┘ä┘ā ┘åž¼ž»┘ć ┘ü┘Ŗ žĄ┘åž»┘ł┘é ┘å┘é┘ł┘ģ ž©žźž▓ž¦žŁž¬┘ć ž╣┘å ┘ģ┘łžČž╣┘ć: ┘䞦 ┘Ŗ┘łž¼ž» ┘üž▒┘é ž©┘Ŗ┘å žŻ┘å ┘åž▓┘ŖžŁ ž¦┘䞥┘åž»┘ł┘é žź┘ä┘ē ž¦┘䞯┘ģž¦┘ģ žŻ┘ł┘䞦 ž½┘ģ žź┘ä┘ē ž¦┘ä┘Ŗ┘ģ┘Ŗ┘å žŻ┘ł žŻ┘å ┘åž▓┘ŖžŁ┘ć ┘ü┘Ŗ ž«žĘ ┘ģž©ž¦ž┤ž▒ ž╣ž▒žČ┘Ŗ ┘ü┘Ŗ ž¦┘䞦ž¬ž¼ž¦┘ć ž¦┘䞯┘ģž¦┘ģ┘Ŗ-ž¦┘ä┘Ŗ┘ģ┘Ŗ┘å┘Ŗ.
┘ü┘Ŗ ┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘ģ
┘Ŗ┘ģž¦ž½┘ä ž¦┘䞬ž▒ž¦┘āž© ┘ü┘Ŗ ┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘ģ ž¦┘䞬ž▒ž¦┘āž© ┘ü┘Ŗ ž¦┘ä┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘䞦ž│┘Ŗ┘ā┘Ŗž® žŁ┘Ŗž½ žŻ┘å ž¦┘䞣ž¦┘䞦ž¬ ž¦┘ä┘ā┘ģ┘ł┘ģ┘Ŗž® ž¬┘łžĄ┘ü žŻ┘ŖžČž¦ ž©ž»┘łž¦┘ä ┘ģ┘łž¼┘Ŗž®. ┘ģž╣ ┘ģ┘䞦žŁžĖž® žŻ┘å ž¦┘äž»┘łž¦┘ä ž¦┘ä┘ā┘ģ┘ł┘ģ┘Ŗž® ž¦┘ä┘ģ┘łž¼┘Ŗž® ┘ä┘Ŗž│ž¬ ┬½žŁ┘é┘Ŗ┘é┘Ŗž®┬╗ ┘ā┘ģž¦ ┘ć┘ł ┘ü┘Ŗ ž¦┘䞣ž¦┘äž® ž¦┘ä┘ā┘䞦ž│┘Ŗ┘ā┘Ŗž®. ┘ü┘Ŗ ┘ģ┘Ŗ┘āž¦┘å┘Ŗ┘āž¦ ž¦┘ä┘ā┘ģ ┘Ŗž╣ž©ž▒ ž╣┘å ž¬ž▒ž¦┘āž© ┘ģž¬ž¼┘枦ž¬ ž¦┘䞣ž¦┘äž® ž©ž¼┘ģž╣ ┘ģž¬ž¼┘枦ž¬.
┘Ŗž╣ž©ž▒ ž╣┘å ž░┘ä┘ā ž▒┘Ŗž¦žČ┘Ŗž¦ ž©ž¦┘䞥┘Ŗž║ž® ┬½ž©ž▒ž¦-┘ā┘Ŗž¬┬╗ Bra-Ket :

ž¬┘ä┘ā ž¦┘ä┘ģž╣ž¦ž»┘äž® ž¬┘é┘ł┘ä žŻ┘å ž¦┘䞣ž¦┘äž® ž¦┘ä┘ā┘ä┘Ŗž®  ž¬ž¬┘ā┘ł┘å ┘ģ┘å ž¬ž▒ž¦┘āž© ž╣ž»ž® žŁž¦┘䞦ž¬
ž¬ž¬┘ā┘ł┘å ┘ģ┘å ž¬ž▒ž¦┘āž© ž╣ž»ž® žŁž¦┘䞦ž¬  ┘łž¬žĄ┘ü┘枦 ž¬┘ģž¦┘ģž¦. ┘ł┘ć┘Ŗ ┘äž░┘ä┘ā ž¬ž│┘ģ┘ē ┬½ž¬ž▒ž¦┘āž© ž¦┘䞣ž¦┘äž®┬╗. ┘üžźž░ž¦ ┘āž¦┘垬 ž¬┘ä┘ā ž¦┘䞣ž¦┘䞦ž¬
┘łž¬žĄ┘ü┘枦 ž¬┘ģž¦┘ģž¦. ┘ł┘ć┘Ŗ ┘äž░┘ä┘ā ž¬ž│┘ģ┘ē ┬½ž¬ž▒ž¦┘āž© ž¦┘䞣ž¦┘äž®┬╗. ┘üžźž░ž¦ ┘āž¦┘垬 ž¬┘ä┘ā ž¦┘䞣ž¦┘䞦ž¬  ┘ģ┘łžŁž»ž® ┘ü┘Ŗ┘ģž¦ ž©┘Ŗ┘å┘枦 ┘üž¬ž╣žĘ┘Ŗ ┘ģž▒ž©ž╣ž¦ž¬ ž¦┘ä┘é┘Ŗ┘ģ
┘ģ┘łžŁž»ž® ┘ü┘Ŗ┘ģž¦ ž©┘Ŗ┘å┘枦 ┘üž¬ž╣žĘ┘Ŗ ┘ģž▒ž©ž╣ž¦ž¬ ž¦┘ä┘é┘Ŗ┘ģ  ┬½ž¦┘ä┘ģžĘž¦┘䞦ž¬ ž¦┘ä┘ģžŁž¬┘ģ┘äž®┬╗
┬½ž¦┘ä┘ģžĘž¦┘䞦ž¬ ž¦┘ä┘ģžŁž¬┘ģ┘äž®┬╗  žī žŻ┘Ŗ ž¬ž╣žĘ┘Ŗ žŻžŁž¬┘ģž¦┘ä ž¦┘䞣žĄ┘ł┘ä ž╣┘ä┘ē ┘垬┘Ŗž¼ž® ž¦┘ä┘é┘Ŗž¦ž│ ┘ü┘Ŗ ž¦┘䞣ž¦┘äž® ž¦┘䞬┘Ŗ ž¬ž«žĄ┘枦.
žī žŻ┘Ŗ ž¬ž╣žĘ┘Ŗ žŻžŁž¬┘ģž¦┘ä ž¦┘䞣žĄ┘ł┘ä ž╣┘ä┘ē ┘垬┘Ŗž¼ž® ž¦┘ä┘é┘Ŗž¦ž│ ┘ü┘Ŗ ž¦┘䞣ž¦┘äž® ž¦┘䞬┘Ŗ ž¬ž«žĄ┘枦.
┘ü┘Ŗ ž¦┘ä┘ā┘ćž▒ž©ž¦žĪ
┘Ŗ┘åžĘž©┘é ┘ģž©ž»žŻ ž¦┘䞬ž▒ž¦┘āž© ž╣┘ä┘ē ž¦┘䞬┘Ŗž¦ž▒ ž¦┘ä┘ā┘ćž▒ž©ž¦ž”┘Ŗ ┘łž╣┘ä┘ē ž¦┘äž¼┘ćž». ┘ā┘ģž¦ ┘Ŗ┘åžĘž©┘é ž╣┘ä┘ē žŁž│ž¦ž©ž¦ž¬ ž¦┘䞬┘Ŗž¦ž▒ ž¦┘ä┘ģž¬ž▒ž»ž» ž¦┘ä┘ģž▒┘āž©ž® ┘䞣ž│ž¦ž© ž¦┘䞬┘Ŗž¦ž▒ ž¦┘ä┘ģž¬ž▒ž»ž» ┘łž¦┘äž¼┘ćž» ž¦┘ä┘ģž¬ž▒ž»ž». ┘ł┘Ŗ┘åžĘž©┘é ž¦┘ä┘ģž©ž»žŻ ž©žĄ┘üž® ž╣ž¦┘ģž® ž╣┘ä┘ē ž¦┘äž»┘łž¦ž”ž▒ ž¦┘ä┘ā┘ćž▒ž©ž¦ž”┘Ŗž® ┘ü┘éžĘ ž¦┘ä┘ģ┘ā┘ł┘åž® ┘ģ┘å ┘łžŁž»ž¦ž¬ ž¬ž╣┘ģ┘ä ž«žĘ┘Ŗž¦.
ž¦┘éž▒žŻ žŻ┘ŖžČž¦
┘ģž▒ž¦ž¼ž╣