قسمة متعددات الحدود
|
Read other articles:

Kenji Sato (佐藤 賢司code: ja is deprecated , Satō Kenji, lahir pada tahun 1963) adalah aktor anak-anak asal Jepang. Dia dikenal dengan peran-perannya dalam serial tokusatsu dan drama: sebagai Akira Sakimori / Zone Junior dalam Ryuusei Ningen Zone. Filmografi Ryuusei Ningen Zone (NTV, 1973) - Akira Sakimori / Zone Junior Kaijin Nijuu Mensou (Fuji TV, 1977) Artikel bertopik biografi Jepang ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Star Ocean: Blue Sphere PublikasiGame Boy ColorJP: June 28, 2001Telepon selulerJP: June 8, 2009GenreAction role-playingKarakteristik teknisPlatformGame Boy Color ModePermainan video pemain tunggal FormatROM cartridge Format kode Daftar 30 Informasi pengembangPengembangtri-AcePenyuntingEnix PengarahYoshiharu GotandaProdusenYoshinori YamagishiDesainerAkira TakayashikiKomponisMotoi SakurabaPenerbitEnixSenimanMayumi AzumaInformasi tambahanSitus websquare-enix.co.jp… MobyGamesstar-ocean-blue-sph...

Domnole du MansVitrail de chœur d'Ernest Lami de Nozan d'après des cartons d'Auguste Galimard, église Saint-Laurent de Paris.BiographieDécès 1er décembre 581Le MansActivités Évêque du Mans (558 - 1er décembre 581), clerc régulierAutres informationsÉtape de canonisation SaintFête 1er décembremodifier - modifier le code - modifier Wikidata Domnole (lat. Domnolus) était évêque du Mans de 558 ou 559 à sa mort le 1er décembre 581 ; le bénédictin Jean Bondonnet, au XVIIe&#...

Pour les articles homonymes, voir Gouvernement fédéral. Gouvernement fédéral de BelgiqueCadreType Gouvernement fédéral (depuis 1993), pouvoir exécutifSiège 16, rue de la LoiPays BelgiqueOrganisationPrésident Alexander De CrooSite web www.gouvernement-federal.bemodifier - modifier le code - modifier Wikidata Le gouvernement fédéral de Belgique constitue l’organe exécutif de la Belgique, sa compétence recouvre tout ce qui a trait à l'intérêt général comme: les finance...

Cycling race 2019 Bredene Koksijde Classic2019 UCI Europe TourRace detailsDates22 March 2019Stages1Distance199.5 km (124.0 mi)Winning time4h 35' 47Results Winner Pascal Ackermann (GER) (Bora–Hansgrohe) Second Kristoffer Halvorsen (NOR) (Team Sky) Third Álvaro Hodeg (COL) (Deceuninck–Quick-Step)← 2018 2021 → The 2019 Bredene Koksijde Classic was the 17th edition of the Bredene Koksijde Classic road cycling...
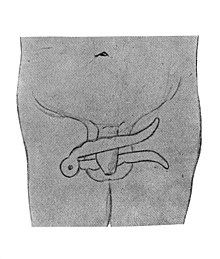
Pour les articles homonymes, voir Circoncision (homonymie). Circoncision Pénis avant et après l'ablation du prépuce. Données clés Organe Pénis Indications pratique religieuse, rite de passage, phimosis, paraphimosis et prophylaxie Première mondiale depuis l'Antiquité CIM-10 PCS 0VBT CIM-9-CM Volume 3 « V50.2 » MeSH « D002944 » modifier La circoncision, en latin : circumcisio, « fait de couper autour, découpe », désigne, dans sa forme la plus...

Euarchontoglires TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaSuperordoEuarchontoglires Ordo Glires Anagaloidea† Arctostylopida† Rodentia Lagomorpha Euarchonta Dermoptera Scandentia Primates Plesiadapiformes† lbs Euarchontoglires (bersinonim Supraprimates) adalah klad dan superordo hewan menyusui, berisikan (diantaranya) lima grup: hewan pengerat, Lagomorpha, tupai, kubung dan primata. Organisasi Hubungan yang masih diteliti:[1] Boreoeutheria Euarchontoglires Gliriformes &...

Sanhe 三河市SanhoKota setingkat countyBlok apartemen di SanheKoordinat: 40°01′N 117°05′E / 40.017°N 117.083°E / 40.017; 117.083Koordinat: 40°01′N 117°05′E / 40.017°N 117.083°E / 40.017; 117.083NegaraRepublik Rakyat TiongkokProvinsiHebeiKota setingkat prefekturLangfangLuas[1] • Kota setingkat county643,0 km2 (2,480 sq mi) • Luas perkotaan169,00 km2 (6,500 sq mi)Popul...

Tapas PaulPaul pada 2019Nama asalতাপস পালLahir(1958-09-19)19 September 1958Chandannagar, West Bengal, IndiaMeninggal18 Februari 2020(2020-02-18) (umur 61)[1]Mumbai, Maharastra, IndiaKebangsaanIndiaPekerjaanPemeran, politisiTahun aktif1980–2013[2]Karya terkenalDadar KirtiBhalobasa Bhalobasa[3]Anurager ChoyanAmar BandhanGuru DakshinaUttaraMondo Meyer UpakhyanPartai politikAll India Trinamool CongressSuami/istriNandini Paul (...

Enrico Fermi, il pioniere italiano sugli studi della fisica nucleare con il gruppo dei Ragazzi di via Panisperna La fisica nucleare è la branca della fisica che studia il nucleo atomico, i suoi costituenti, protoni e neutroni, e le loro interazioni. Si distingue dalla fisica atomica, di cui è una sottobranca, che studia l'atomo nella sua interezza, e dalla fisica delle particelle, che ha come oggetto lo studio delle singole particelle libere. Questa branca ha in larga parte soppiantato il t...

American software company This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ashton-Tate – news · newspapers · books · scholar · JSTOR (August 2012) (Learn ho...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Lower house of the Maryland General Assembly This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2012) (Learn how and when to remove this message) Maryland House of DelegatesMaryland General AssemblyTypeTypeLower house Term limitsNoneHistoryNew session startedJanuary 11, 2023LeadershipSpeakerAdrienne Jones (D) since April 7, 2019 Speaker pro temporeDana St...

الدوري البرتغالي الممتاز 1988-89 تفاصيل الموسم الدوري البرتغالي الممتاز النسخة 51 البلد البرتغال المنظم اتحاد البرتغال لكرة القدم البطل نادي بنفيكا مباريات ملعوبة 380 عدد المشاركين 20 الدوري البرتغالي الممتاز 1987-88 الدوري البرتغالي الممتاز 1989-90 ت�...

American musician (1958–2016) This article is about the American singer and musician. For other uses, see Prince (disambiguation). PrincePrince in 1981BornPrince Rogers Nelson(1958-06-07)June 7, 1958Minneapolis, MinnesotaDiedApril 21, 2016(2016-04-21) (aged 57)Chanhassen, MinnesotaCause of deathAccidental fentanyl overdoseOther names The Artist (Formerly Known as Prince) (TAFKAP) Camille Occupations Singer songwriter musician record producer actor Years active1975–2016...

City in Yaroslavl Oblast, Russia For other places with the same name, see Yaroslavl (inhabited locality). For the Sakhalin Shipping Company's steamship, see SS Yaroslavl. City in Yaroslavl Oblast, RussiaYaroslavl ЯрославльCity[1]Clockwise, from top right: St. Alexander Nevsky's Chapel, St. John the Baptist's Church, Strelka Park from Volga Embankment, Znamenskaya Tower, Volkov Theater, St. Elijah the Prophet's Church FlagCoat of armsLocation of Yaroslavl YaroslavlLocation of ...

Sculpture by Gian Lorenzo Bernini and Alessandro Algardi Statue of Carlo BarberiniArtistGian Lorenzo Bernini, Alessandro AlgardiYear1630Catalogue27TypeSculptureMediumMarbleLocationPalazzo dei Conservatori, RomePreceded byMemorial to Carlo BarberiniFollowed byCharity with Four Children The Statue of Carlo Barberini was a large statue of the brother of Pope Urban VIII, Carlo Barberini, erected in the Palazzo dei Conservatori, Rome, following his death in 1630. The statue made use of a...

CiemasKecamatanCiemasPeta lokasi Kecamatan CiemasTampilkan peta Kabupaten SukabumiCiemasCiemas (Jawa Barat)Tampilkan peta Jawa BaratCiemasCiemas (Jawa)Tampilkan peta JawaCiemasCiemas (Indonesia)Tampilkan peta IndonesiaKoordinat: 7°13′57″S 106°31′06″E / 7.2326114492727385°S 106.51845384395807°E / -7.2326114492727385; 106.51845384395807Negara IndonesiaProvinsiJawa BaratKabupatenSukabumiPemerintahan • CamatIwan MuhdiawanPopulasi • ...

ميّز عن عدسة مكبرة. مجموعة من العدسات المقربة العدسة المقربة في مجال التصوير الضوئي والتصوير السينمائي هي عدسة خاص من العدسات طويلة البعد البؤري يكون فيها الطول الفيزيائي للعدسة أقصر من البعد البؤري.[1] وبذلك يمكن لهذه العدسات أن تقوم بالتقريب بشكل مناظر للمقراب...
