قانوني فيك للانتشار
|
Read other articles:

Irene MonteroMP Kementerian KesetaraanPetahanaMulai menjabat 13 Januari 2020Penguasa monarkiFelipe VIPerdana MenteriPedro Sánchez PendahuluCarmen Calvo(Presidensi, Hubungan dengan Cortes dan Kesetaraan)PenggantiPetahanaAnggota Kongres DeputiPetahanaMulai menjabat 13 Januari 2016Daerah pemilihanMadrid Informasi pribadiLahir13 Februari 1988 (umur 36)Madrid, SpanyolPartai politikPodemos (2014–sekarang)Afiliasi politiklainnyaPersatuan Pemuda Komunis Spanyol (2004–?)Pasangan seru...

Kamen Rider SeriesSebuah Patung Kamen Rider 1 di halaman depan Gedung Kantor Bandai di Taitō, TokyoDiciptakan olehShotaro IshinomoriIshimori ProductionsToei CompanyKarya asliKamen RiderPemilikIshimori ProductionsTV Asahi (1971–1975, Era Shōwa, hingga penanyangan Amazon, 2000-sekarang, Era Heisei)MBS/TBS (1975-1989, Era Shōwa, dari penanyangan Stronger hingga penanyangan Black RX)ADK (2000-sekarang)Toei CompanyToei Advertising (1979–sekarang)Film dan televisiFilmSee belowSeri televisiSe...

TanjidorTanjidorDikembangkanIndonesiaInstrumen terkait Gambang kromong, Keroncong Tanjidor (kadang hanya disebut tanji) adalah sebuah kesenian Betawi yang berbentuk orkes. Kesenian ini sudah dimulai sejak abad ke-19 atas rintisan Augustijn Michiels atau lebih dikenal dengan nama Mayor Jantje di daerah Citrap atau Citeureup.[1] Alat-alat musik yang digunakan biasanya sama seperti drumben. Kesenian Tanjidor juga terdapat di Kalimantan Barat, sementara di Kalimantan Selatan sudah punah. ...

المعهد القومي لأبحاث الأمراض المتوطنة والكبد - قصر العيني المرض الوافد[1] والمرض المتوطن والمرض البلادي[2] في علم الوبائيات هو المرض الطارئ الذي ينتشر في تجمع بدون الحاجة إلى عواملَ خارجية. فعلى سبيل المثال، (مرض الهزال المزمن) أو مرض الحُماق (أو جدري الماء) مرض متوطن...

Questa voce o sezione sull'argomento politici francesi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento politici francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Marcel Cachin Marce...

Major watercourse in northwestern North America Yukon RiverCanoeing the Yukon RiverLocation of the Yukon River and watershedNative nameŲųg Han (Gwichʼin)Yuk Han (Gwichʼin)Kuigpak (Central Yupik)Kuukpak (Inupiaq)Yeqin (Degexit'an)Tth'echù' (Hän)Chuu k'onn (Hän)Chu Nìikwän (Southern Tutchone)LocationCountriesUnited StatesCanadaStateAlaskaProvince/TerritoryBritish ColumbiaYukonPhysical characteristicsSourceLlewellyn Glacier at Atlin Lake ...

Gas-turbine powered vehicle used to set a world land speed record Motor vehicle Bluebird-Proteus CN7Bluebird today at BeaulieuOverviewManufacturerMotor Panels[1]Also calledProteus-Bluebird Campbell–Norris 7Production1[1]DesignerKen Norris[1]Body and chassisBody stylestreamlined fully enclosed turtle shellLayoutfour-wheel drive centre enginedPowertrainEngineA Bristol-Siddeley Proteus 705 free-turbine turboshaft) engine of 4,450 shp (3,320 kW)[1...

Об издательстве см. Амфора (издательство). Амфора, зарываемая в песок в трюме корабля, предназначенная для перевозки (оливкового масла, вина, зерна). Особый (остроконечный) вид дна амфоры обусловлен стремлением избежать разрушения из-за качки, а особый вид горловины о...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
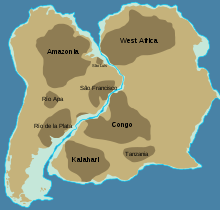
Cerro Batoví is an erosional remnant made up of flood basalt overlying sedimentary rocks. Approximate location of Mesoproterozoic (older than 1.3 Ga) cratons in South America and Africa The geology of Uruguay combines areas of Precambrian-aged shield units with a region of volcanic rock erupted during the Cretaceous and copious sedimentary facies the oldest of which date from the Devonian. Big events that have shaped the geology of Uruguay include the Transamazonian orogeny (2000 millio...

[1]Bagian dari seri artikel mengenaiSyiah Peribadatan Penerus Nabi Muhammad Imamah Duka Muharram Tawassul Paham Kebohongan Ayatullah Arbain Hari perayaan Syiah Asyura Tabuik Arbain Maulud Idulfitri Iduladha Idulghadir Sejarah Ayat pemurnian Hadits dua hal berat Mubāhalah Khumm Rumah Fatimah Fitnah Pertama Fitnah Kedua Pembunuhan Ali Pertempuran Karbala Cabang-cabang Syiah Zaidiyah Syiah Dua Belas Imam Ja'fari Akhbari Syaiki Usuli Batini Alevi Bektashi Ghulat Alawi Hurufi Qizilbash Is...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Jacques SéveracLahir1902Meninggal1982PekerjaanSutradaraPenulis naskahTahun aktif1928-1962 Jacques Séverac (1902–1982) adalah seorang sutradara dan penulis naskah asal Prancis. Ia menyutradarai 21 film antara 1928 dan 1962. Film buatannya Chil...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Seize quartiers – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this message) Seize quartiers ahnentafel document (1786). Seize quartiers is a French phrase which literally means a person's sixteen quarters, the coats ...

Province of the Sasanian Empire Sasanian province of YemenYamanProvince of the Sasanian Empire570–628Map of the Sasanian Empire, with Yemen located in the southern part of the Arabian PeninsulaCapitalSana'aHistorical eraAntiquity• Sasanian conquest of Yemen 570• 570• The Sasanian nobles make an alliance with Muhammad 628 Preceded by Succeeded by Kingdom of Aksum Muhammad in Medina Today part ofYemen Part of a series on the History of Yemen Timeline Ancient history King...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) مصطفى الشطي معلومات شخصية الاسم الكامل مصطفى بن أحمد بن حسن الشطي الميلاد سنة 1856 دمشق الوفاة سنة 1929 (72...

Энделиента Дата рождения V век Место рождения Корнуолл[вд], Cornwall[вд], Юго-Западная Англия, Англия Дата смерти VI век Место смерти Корнуолл, Англия Род деятельности религиозный лидер Отец Бринах Мать Cymorth[вд] Энделиента (Endelienta, Endelient, Edellienta) или Энделлион (Endellion) (VI) — ...

Yang Mulia PausTheodoros IIPaus Gereja Ortodoks Koptik Aleksandria dan seluruh MesirPaus Theodoros IINama asalTheodoros IIⲠⲁⲡⲁ Ⲁⲃⲃⲁ Ⲑⲉόⲇⲱⲣⲟⲥالبابا تواضروس التانىGerejaGereja Ortodoks Koptik AleksandriaTakhtaTahta St. MarkusAwal masa kepausan18 November 2012[1]PendahuluPaus Shenouda IIIImamatTahbisan imam1989[1]Tahbisan uskup15 Juni 1997Informasi pribadiNama lahirWagih Subhi Baqi Sulaymanوجيه صبحى باقى سليمانLa...

1918 song After You've GoneSheet music cover (1918)SongPublished1918Composer(s)Turner LaytonLyricist(s)Henry Creamer After You've Gone Instrumental performance by musicians from the U.S. Coast Guard Band Problems playing this file? See media help. After You've Gone is a 1918 popular song composed by Turner Layton with lyrics by Henry Creamer.[1] History It was recorded by Marion Harris on July 22, 1918, and released by Victor Records.[2] The song became so popular that the she...

Emblematic arch common in Moorish architecture Horseshoe arch The horseshoe arch (Arabic: قوس حدوة الحصان; Spanish: arco de herradura), also called the Moorish arch and the keyhole arch, is a type of arch in which the circular curve is continued below the horizontal line of its diameter, so that the opening at the bottom of the arch is narrower than the arch's full span.[1][2][3] Evidence for the earliest uses of this form are found in Late Antique and Sas...















































