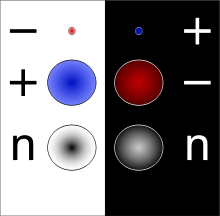جسيم مضاد
|
Read other articles:

كوبا سودأمريكانا معلومات عامة الرياضة كرة القدم انطلقت 2002 المنظم اتحاد أمريكا الجنوبية لكرة القدم المنطقة أمريكا الجنوبية عدد النسخ 20 نسخة التواتر سنوية عدد المشاركين 10 اتحادات قارية وضع المشاركين محترفون الموقع الرسمي الموقع الرسمي قائمة الفائزين أخر بطل ليغا دو ك�...

County in Colorado, United States County in ColoradoEagle CountyCountyThe Eagle County Justice Center (county courthouse) in Eagle FlagLocation within the U.S. state of ColoradoColorado's location within the U.S.Coordinates: 39°37′N 106°42′W / 39.62°N 106.7°W / 39.62; -106.7Country United StatesState ColoradoFoundedFebruary 11, 1883Named forEagle RiverSeatEagleLargest communityEdwardsArea • Total1,692 sq mi (4,380 km2) ...

حديقة الجزيرة الملكية الوطنية IUCN التصنيف V (منظر طبيعي أو بحري محمي) صورة لطائرة اثناء الهبوط على المياه المحيطة بالحديقة البلد الولايات المتحدة[1] الموقع مقاطعة كيويناو (ميشيغان)، الولايات المتحدة أقرب مدينة ثاندر باي (أونتاريو) إحداثيات 48°01′N 88°51′W / 48.01°N ...

Building in New York City, United States of AmericaThe Church of the Immaculate Conception of the Blessed Virgin MaryImmaculate Conception Church East 150th StreetGeneral informationArchitectural styleRomanesque RevivalTown or cityMelrose, Bronx, New York CityCountryUnited States of AmericaCompleted1887 (for church)[1][2]1901 (for school hall)[1]ClientRoman Catholic Archdiocese of New YorkTechnical detailsStructural systemBrick masonryDesign and constructionArchitect(s...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

NavoiyNavoiyLocation in UzbekistanKoordinat: 40°05′04″N 65°22′45″E / 40.08444°N 65.37917°E / 40.08444; 65.37917Koordinat: 40°05′04″N 65°22′45″E / 40.08444°N 65.37917°E / 40.08444; 65.37917Negara UzbekistanRegionRegion NavoiyDistrikDistrik NavoiyStatus kota3 September 1958Pemerintahan • Hokim (gubernur)Tursununov Qobil BeknazarovichLuas • Total35 km2 (14 sq mi)Ketinggian382 m (1,...

Decorative objects made from clay and other raw materials by the process of pottery Etruscan: Diomedes and Polyxena, from the Etruscan amphora of the Pontic group, c. 540–530 BCE – From Vulci The Music Lesson, gold anchor, Chelsea porcelain, c. 1765, with bocage background. 15 3/8 × 12 1/4 × 8 3/4 inches, 22 lb. (39.1 × 31.1 × 22.2 cm, 10 kg). different version, different angle. Chinese Jun ware wheel-thrown stoneware bowl with blue glaze and purple splashes, ...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this message) Schedule 1 substances, in the sense of the Chemical Weapons Convention, are chemicals which are feasible either to be used directly as chemical weapons or in the manufacture of chemical weapons, and which have very limited to no use outside of chemical w...

Breadth of ideas which can be represented in a formal language In computer science, the expressive power (also called expressiveness or expressivity) of a language is the breadth of ideas that can be represented and communicated in that language. The more expressive a language is, the greater the variety and quantity of ideas it can be used to represent. For example, the Web Ontology Language expression language profile (OWL2 EL) lacks ideas (such as negation) that can be expressed in OWL2 RL...

Carte des six comtés métropolitains de l'Angleterre. Un comté métropolitain (en anglais : metropolitan county) est un type de subdivision de l'Angleterre. Il en existe six qui couvrent principalement des aires urbaines : Grand Manchester (Manchester) Merseyside (Liverpool), Yorkshire du Sud (Sheffield), Tyne and Wear (Newcastle upon Tyne), Midlands de l'Ouest (Birmingham) Yorkshire de l'Ouest (Leeds) Les comtés métropolitains sont créés en 1974 et sont eux-mêmes divisés en...
9 South African Infantry Battalion9 SAI emblemCountry South AfricaBranch South African ArmyTypeMotorised infantry (seaborne)Part ofSouth African Infantry FormationGarrison/HQCape Town, Western CapeMotto(s) Fortiter et fideliter (Boldly and faithfully) Ebenhaeser (Thus far the Lord has led us) Battle honours Cape of Good Hope[a] Kilimanjaro[b][c] Behobeho Nvangao East Africa 1916-7 East Africa 1917-8 Megiddo Nablus Palestine 1918 InsigniaCompany lev...

2001 IAAF WorldIndoor ChampionshipsTrack events60 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen3000 mmenwomen60 m hurdlesmenwomen4 × 400 m relaymenwomenField eventsHigh jumpmenwomenPole vaultmenwomenLong jumpmenwomenTriple jumpmenwomenShot putmenwomenCombined eventsPentathlonwomenHeptathlonmenvte The men's 60 metres event at the 2001 IAAF World Indoor Championships was held on March 11. Medalists Gold Silver Bronze Tim Harden United States Tim Montgomery Unite...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) جزء من سلسلة مقالات سياسة هولنداهولندا الدستور الدستور ميثاق مملكة الأراضي المنخفضة قانون الأحكام العا�...

American racing driver Ryan NormanNorman during Indy Lights qualifying at Portland in 2018Nationality AmericanBorn (1998-03-19) March 19, 1998 (age 26)Aurora, OhioMichelin Pilot Challenge careerCurrent teamBryan Herta AutosportCar number88Previous series2016 2014-2015Atlantic Championship Formula Enterprises Skip Barber Winter SeriesChampionship titles2016 2020Formula Atlantic Champion IMSA Michelin Pilot TCR ChampionIndyCar Series career1 race run over 1 yearTeam(s)No. 52 (Dale Coyne Ra...

Species of rodent Richardson's ground squirrel Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Rodentia Family: Sciuridae Genus: Urocitellus Species: U. richardsonii Binomial name Urocitellus richardsonii(Sabine, 1822) Synonyms Spermophilus richardsonii Richardson's ground squirrel (Urocitellus richardsonii), also known as the dakrat or flickertail, is a North American ...

English textile artist, author, and socialist (1834–1896) For other people named William Morris, see William Morris (disambiguation). William MorrisWilliam Morris by Frederick Hollyer, 1887Born(1834-03-24)24 March 1834Walthamstow, Essex, EnglandDied3 October 1896(1896-10-03) (aged 62)Hammersmith, EnglandEducationExeter College, OxfordOccupationsTextile designerpoettranslatorsocialist activistKnown forWallpaper and textile designfantasy fictionmedievalismsocialismNotable workNews f...

English mathematician For other people with the same name, see Phil Hall (disambiguation). Not to be confused with Marshall Hall (mathematician). Philip HallPhilip HallBorn(1904-04-11)11 April 1904London, EnglandDied30 December 1982(1982-12-30) (aged 78)Cambridge, EnglandAlma materUniversity of CambridgeKnown forHall's marriage theoremHall polynomialHall subgroupHall–Littlewood polynomialAwardsSenior Berwick Prize (1958)Sylvester Medal (1961)Larmor Prize (1965)De Morgan Medal...

В Википедии есть статьи о других людях с фамилией Ковач. Лайош Ковач Полное имя Лайош Немеш Ковач Родился 27 апреля 1894(1894-04-27)Будапешт, Венгрия Умер 17 декабря 1961(1961-12-17) (67 лет)Нью-Йорк, Нью-Йорк, США Гражданство Венгрия Позиция защитник Клубная карьера[* 1] МТК 1925—1927 Но...

Protests in Kyiv, 2014 See also: Euromaidan and Timeline of the Euromaidan 2014 Hrushevsky Street protestsPart of Euromaidan and Revolution of DignityHrushevsky street protests in January 2014Date19–22 January 2014 (protests)[1][2][3]23 January – 17 February 2014 (standoff)18–23 February 2014 (escalation) (1 month)LocationHrushevsky Street, Kyiv, Ukraine50°27′02″N 30°31′47″E / 50.450417°N 30.529586°E / 50.450417; 30.529586Cause...

Hình họcHình chiếu một mặt cầu lên mặt phẳng. Đại cươngLịch sử Phân nhánh Euclid Phi Euclid Elliptic Cầu Hyperbol Hình học phi Archimedes Chiếu Afin Tổng hợp Giải tích Đại số Số học Diophantos Vi phân Riemann Symplectic Phức Hữu hạn Rời rạc Kỹ thuật số Lồi Tính toán Fractal Liên thuộc Khái niệmChiều Phép dựng hình bằng thước kẻ và compa Đỉnh Đường cong Đường chéo Góc Song song Vuông góc ...