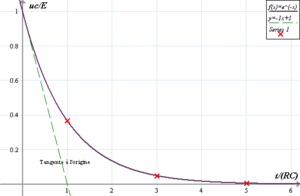
تضاؤل أسي
|
Read other articles:
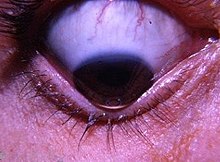
Medical condition involving the eye Not to be confused with Ketyconus. Medical conditionKeratoconusOther namesKC, KCN, conical cornea[1]The cone shaped cornea that is characteristic of keratoconusPronunciationKEHR-uh- toh-KOH-nus[2] SpecialtyOphthalmology, optometrySymptomsBlurry vision, nearsightedness, light sensitivity[3]Usual onsetEarly adulthood[3]CausesUnknown[3]Diagnostic methodSlit lamp exam[3]TreatmentGlasses, contacts, surgery[...

Mapa étnico de Yemen Según World Population,[1] en Yemen había, en 2019, 29.388.000 hab., con una densidad de 53,5 hab/km². La población urbana era del 35,2%, con un máximo en la capital, Saná, de 3,937.000 hab. Ciudades como Taiz, Al Hudayda y Aden tienen en torno a 500.000 hab. La mayor parte de los yemeníes es de origen árabe; no obstante, es una sociedad fuertemente tribal, con cerca de 400 tribus zaidinas o zaidíes en el norte y grupos de castas hereditarias en las zonas...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

2003 video gameResident Evil: Dead AimNorth American box artDeveloper(s)CaviaPublisher(s)CapcomDirector(s)Eiro ShirahamaTakuya IwasakiProducer(s)Tatsuya MinamiKouji NakajimaHideshi TatsunoDesigner(s)Yōichi TakeHisao AkakiTakumi KudōTadayuki HoshinoAtsushi KuwaharaWriter(s)Noboru SugimuraJunichi MiyashitaToyokazu SakamotoComposer(s)Nobuyoshi SanoSeriesResident EvilPlatform(s)PlayStation 2ReleaseJP: February 13, 2003NA: June 17, 2003PAL: July 11, 2003[1]Genre(s)Light gun shooterMode(s...

Red Bull RB15 La Red Bull RB15 di Max Verstappen Descrizione generale Costruttore Red Bull Racing Categoria Formula 1 Squadra Aston Martin Red Bull Racing Progettata da Adrian NeweyRob MarshallPierre WachéSteve WinstanleyDave WornerBen WaterhouseDan FallowsCraig Skinner Sostituisce Red Bull RB14 Sostituita da Red Bull RB16 Descrizione tecnica Meccanica Telaio Monoscocca in Fibra di carbonio Motore Honda RA619H, V6 1.6 a 90° Turbo Ibrido Trasmissione Cambio sequenziale a 8 rapporti + ...

German mathematician (1845–1918) Georg CantorCantor, c. 1910BornGeorg Ferdinand Ludwig Philipp Cantor(1845-03-03)3 March 1845Saint Petersburg, Russian EmpireDied6 January 1918(1918-01-06) (aged 72)Halle, Province of Saxony, German EmpireNationalityGerman-RussianAlma mater Swiss Federal Polytechnic University of Berlin University of Göttingen Known forSet theorySpouse Vally Guttmann (m. 1874)AwardsSylvester Medal (1904)Scientific careerFie...

Le filet à papillon de Vladimir Nabokov, romancier et lépidoptériste Un lépidoptériste est un spécialiste des lépidoptères. Le terme inclut aussi les amateurs qui capturent, collectent, étudient ou simplement observent les lépidoptères[1]. Historique L'accroissement du nombre de lépidoptéristes après la Renaissance peut être attribué à un intérêt croissant pour la science et la nature. Quand Carl von Linné écrivit la dixième édition du Systema Naturae en 1758, il y ava...

Condiment made from fish Fish sauceTypeCondimentPlace of originVarious placesRegion or stateSoutheast Asia and East AsiaAssociated cuisineMyanmar, Cambodia, China, Laos, Philippines, Thailand, and VietnamMain ingredientsFish, salt Media: Fish sauce Part of a series onChinese cuisine Regional cuisines Four Great Traditions Chuan (Sichuan) Lu (Shandong) Yue (Guangdong) Huaiyang (Jiangsu) Eight Great Traditions(+all above) Anhui Fujian Hunan Zhejiang Ten Great Traditions(+all above) Be...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

2nd-century homily of Melito of Sardis Papyrus with fragments of Book of Enoch and Peri Pascha. A decorative flourish marks the end of 'Book of Enoch' and the beginning of the 'Peri Pascha'. This simple embellishment represents some of the earliest ornamentation of Christian codices. Egypt, 4th century. Chester Beatty Library Peri Pascha (Greek: Περί Πάσχα) (English title On the Pascha) is a 2nd-century homily of Melito of Sardis written between A.D.160 and 170 in Asia Minor. It was ...

Ethnic group Chinese people in East TimorA mix wedding of East Timorese and Chinese Hakka people in East Timor, where the four flower girls and the mother of the bride on the far right are of Chinese Hakka descent.Total population4,000[1]—20,000 (Historically)Regions with significant populations East Timor AustraliaLanguagesPortuguese, Indonesian, Chinese (Hakka, Cantonese, Mandarin), Tetum, MacaneseReligionConfucianism, Buddhism, Taoism, CatholicismRelated ethnic groupsC...

حزمة عدسية الاسم العلميfasciculus lenticularis تبيّن الصورة مسارات الدوبامين في دماغ الإنسان في الحالة الطبيعية (يسار) ومرض باركنسونز (يمين). تشير الأسهم الحمراء إلى كبت الهدف، والأسهم الزرقاء تشير إلى تحفيز بنية الهدف. الحزمة العدسية مرئية لكنها غير معنونة في الصورة. تفاصيل ترمينول...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الشارع المستقيممعلومات عامةالموقع دمشق، سورياالتقسيم الإداري دمشق البلد سوريا الطول 1570مالإحداثيات ...

Fondazione NobelNobelstiftelsen Ritratto di Alfred Nobel, di Gösta Florman TipoFondazione Fondazione29 giugno 1900 e 1900 FondatoreAlfred Nobel ScopoAmministrare il patrimonio lasciato da Alfred Nobel per l'assegnazione dei Premi Nobel Sede centrale Stoccolma Patrimonio443 000 000 $ (2016) Sito web Modifica dati su Wikidata · Manuale La Fondazione Nobel (in lingua svedese Nobelstiftelsen) è un'istituzione privata creata nel 1900 sulla base delle ultime volontà di Alfred Nobel. Ammini...

Suiza en los Juegos Olímpicos Bandera de SuizaCódigo COI SUICON Asociación Olímpica Suiza(pág. web)Medallas 116 126 131 373 Historia olímpicaJuegos de verano 1896 • 1900 • 1904 • 1908 • 1912 • 1920 • 1924 • 1928 • 1932 • 1936 • 1948 • 1952 • 1956 • 1960 • 1964 • 1968 • 1972 • 1976 • 1980 ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 4th Commando Battalion Belgium – news · newspapers · books · scholar · JSTOR (November 2012) (Learn how and when to remove this message) 4th Commando Battalion (1959-1962)4th (Reserve) Commando Battalion (c.1970-1979)Active1959-62,c.1970-79CountryBelgiumBr...

Gilead Sciences, Inc. Тип Публичная компания Листинг на бирже NASDAQ: GILD Основание 1987 Основатели Майкл Риордан Расположение США: Фостер-сити, Калифорния Ключевые фигуры Дэниэл О’Дэй (председатель совета директоров и CEO)[1] Отрасль Фармацевтическая промышленность Продукция Desc...

Questa voce sull'argomento calciatori cechi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Karel KulaNazionalità Cecoslovacchia Rep. Ceca (dal 1993) Altezza181 cm Calcio RuoloAllenatore (ex centrocampista) Termine carriera1998 - giocatore CarrieraSquadre di club1 1980-1982 Baník Ostrava OKD2 (2)1982-1984 Dukla B.B.19 (1)1984-1991 Baník Ostrava OKD186 (25)1991-1992 Kick...

Region in northeastern Nepal For other uses, see Khumbu (disambiguation). Map of the Khumbu region Khumbu (also known as the Everest Region)[1] is a region of northeastern Nepal on the Nepalese side of Mount Everest. It is part of the Solukhumbu District, which in turn is part of Koshi Pradesh.[2] Khumbu is one of three subregions of the main Kirat Kulung and Sherpa settlement of the Himalaya, the other two being Solu and Pharak. It includes the town of Namche Bazaar as well a...

Pour l’article homonyme, voir Les Mohicans de Paris (série télévisée). Les Mohicans de Paris Jean Taureau dans Les Mohicans de Paris, illustration de Philippoteaux, 1863. Auteur Alexandre Dumas Pays France Genre Roman historique Éditeur Alexandre Cadot Lieu de parution Paris Date de parution 1854-1859 modifier Les Mohicans de Paris est un roman d'Alexandre Dumas publié de 1854 à 1859. Ce roman paraît en feuilleton, de 1854 à 1859, dans le journal fondé par Dumas lui-même, ...