Tiram berduri

Tiram berduri
Spondylus varius

Taksonomi
Galat Lua: callParserFunction: function "Template" was not found.
Spesies	Spondylus varius

Spondylus varius atau tiram berduri atau tiram berduri variabel raksasa merupakan kelompok biota laut yang tergolong dalam famili spondylidae^[1]. Ukurannya relatif besar dibandingkan spesies spondylid lainnya dan tumbuh sekitar 38-50 cm. Spesies ini dapat menghasilkan ruang berisi gas air. Spondylus varius hidup menempel di terumbu berbatu dari daerah pasang surut pada kedalaman 10-50 meter.

Wilayah penemuan

Berstatus Critically Endangered (CR)

Penelitian terbaru terkait habitat Spondylus varius terletak di wilayah Teluk Lianga, Surigao Del Sur, Mindanao Timur dan Filipina yang dilakukan sejak September 2018 hingga Oktober 2019. Terdapat 379 individu yang berhasil dikumpulkan dengan jumlah Jantan sekitar 188 individu dan betina 191 individu. Spesies yang ditemukan bersifat gonorik dan tidak hermafrodit. Kini, spesies bivalvia ini berstatus Critically Endangered (CR) yang terdata pada IUCN Red-list.

Klasifikasi

Kingdom: Animalia

Filum: Moluska

Class: Bivalvia

Famili: Spondylidae

Genus: Spondylus

Spesies: Spondylus varius^[2]

Siklus reproduksi

Tahapan reproduksi^[3] pada periode pengambilan sampel (September 2018-Oktober) menunjukkan adanya sinkronisasi waktu pemijahan^[4] pada jantan dan betina. Puncak berkelanjutan teramati pada bulan Desember 2018 hingga April dengan puncak tertinggi tercatat pada bulan April yang menunjukkan periode aktivitas pemijahan yang relatif lama yaitu beberapa bulan. Setelah masa pemijahan yang panjang ini, dari Agustus hingga Oktober, tahap gametogenesis awal dan akhir mendominasi.

Ukuran gonad matang pada S. varius adalah sekitar 80-100 mm pada panjang cangkang, meskipun beberapa individu mungkin mulai memijah pada panjang cangkang 65 mm. Dalam hal tindakan pengelolaan, disarankan untuk menyisakan sebagian individu yang sudah matang secara reproduktif dalam populasi agar dapat berkembang biak dan merekrut. Oleh karena itu, pada spesies ini, pengumpulan individu yang berukuran kurang dari 65 mm harus dilarang, dan pengumpulan juga harus diatur selama bulan-bulan pematangan dan pemijahan.

Referensi

^ "WoRMS - World Register of Marine Species - Spondylidae Gray, 1826". www.marinespecies.org. Diakses tanggal 2024-05-27.
^ "WoRMS - World Register of Marine Species - Spondylus varius G. B. Sowerby I, 1827". www.marinespecies.org. Diakses tanggal 2024-05-27.
^ Biology, International Journal of Aquatic (2023-12-28). "Reproductive Cycle of Spondylus varius (Sowerby, 1827) in Lianga Bay, Surigao Del Sur, Eastern Mindanao, Philippines | International Journal of Aquatic Biology" (dalam bahasa Inggris).
^ Erika, Adelia; Hudatwi, Mu'alimah; Akhrianti, Irma (2022-11-01). "Identifikasi Jenis Bivalvia Pada Ekosistem Mangrove Di Sekitar Perairan Kota Pangkalpinang". Journal of Marine Research. 11 (4): 695–705. doi:10.14710/jmr.v11i4.34036. ISSN 2407-7690.

Read other articles:

List of University of Cape Town faculty

For alumni of the University of Cape Town, see List of alumni of the University of Cape Town. This list of University of Cape Town faculty includes current, emeritus, former, and deceased professors, lecturers, and researchers. Faculty members who have become Institute Professors, or have earned other significant awards and made significant contributions are listed below. Commerce William Harold Hutt, professor of Commerce and originator of the term Consumer Surplus. Francis Wilson, founded ...

Zee News

Zee NewsDiluncurkan1992PemilikZee News LimitedNegara IndiaBahasaHindiKantor pusatEssel Studio, FC-19, Sector 16-A, Noida, IndiaSaluran seindukZee BusinessZee Punjabi 24 Ghanta Zee 24 TaasSitus webZeenews.com Zee News adalah saluran televisi berita dan urusan publik 24-jam berbahasa Hindi pertama di India, diluncurkan pada tahun 1992. Saluran ini dimiliki oleh Zee News Limited, yang merupakan bagian dari Essel Group. Program terkenal Cinema A to Zee The Inside Story Saluran saudara Zee Ne...

Ghazan

Untuk desa di Iran, lihat Ghazan, Iran. Ghazan yang AgungKhanpādishāh-i Īrān wa Islām (Persia)[1]Ghazan (tengah) terlahir sebagai seorang Kristen, yang belajar Buddha dan menjadi seorang Buddhis, dan beralih keyakinan ke Islam sebagai bagian dari perjanjian militer saat naik takhta.Berkuasa1295– 11 Mei 1304PendahuluBayduPenerusÖljeitüKelahiran5 November 1271Kematian11 Mei 1304(1304-05-11) (umur 32)Nama lengkapMahmud GhazanAyahArghunIbuQuthluq KhatunPermaisuriKököchinAg...

Lovisa Grant

Lovisa Grant Nazionalità Svezia Sci alpino Specialità Slalom gigante, slalom speciale, combinata Squadra IFK Lidingö SLK Termine carriera 2017 Palmarès Competizione Ori Argenti Bronzi Mondiali juniores 0 1 0 Per maggiori dettagli vedi qui Modifica dati su Wikidata · Manuale Lovisa Grant (6 marzo 1995) è un'ex sciatrice alpina svedese. Indice 1 Biografia 2 Palmarès 2.1 Mondiali juniores 2.2 Coppa Europa 2.3 Campionati svedesi 3 Collegamenti esterni Biografia Attiva in...

Francesco di Sales

San Francesco di SalesFrancesco di Sales in un ritratto realizzato tra 1691 e 1700 circa, ad opera di Francisco Ignacio Ruiz de la Iglesia. Vescovo e Dottore della Chiesa NascitaThorens-Glières, 21 agosto 1567 MorteLione, 28 dicembre 1622 (55 anni) Venerato daChiesa cattolica, Comunione anglicana Beatificazione8 gennaio 1662 da papa Alessandro VII Canonizzazione19 aprile 1665 da papa Alessandro VII Santuario principaleBasilica della Visitazione, Annecy (Francia) Ricorrenza24 ...

Maurer-Union

German car maker 1902 Maurer-Union Maurer-Union was a German car maker located in Nuremberg.[1] From 1900–1910, Maurer-Union produced 300 to 400 cars per year. It was one of the first manufacturers that introduced continuously variable transmission using a friction drive.[citation needed] References ^ Le Claire, Gregor (25 February 2009). Nürnberger Autopionier erfand Automatik mit [Nuremberg car pioneer co-invented automatic transmission]. Nürnberger Nachrichten (...

Para Pencari Tuhan Jilid 15: Ke Surga, Yuk!

Para Pencari Tuhan: Jilid 15PosterDibintangi Deddy Mizwar Tio Pakusadewo Jarwo Kwat Irma Annisa Asrul Dahlan Udin Nganga Lavicky Nicholas Bimasena Dinda Kirana Salma Paramitha Yurike Prastika Opie Kumis Cok Simbara Tohir Jokasmo Arswendy Beningswara Ridwan Ghani Dea Lestari Ozzol Ramdan Negara asalIndonesiaJml. episode29RilisJaringan asliSCTV Ajwa TVTanggal disiarkan3 April (2022-04-03) –1 Mei 2022 (2022-5-1)Kronologi musim← SebelumnyaJilid 14 Berikutnya →Jilid ...

Семикаракорск

ГородСемикаракорскСемикаракорск Перекрёсток улиц Авилова и Зелёного переулка, 2018 год Герб 47°31′00″ с. ш. 40°48′00″ в. д.HGЯO Страна Россия Субъект Федерации Ростовская область Муниципальный район Семикаракорский Городское поселение Семикаракорское Глава Нау...

博里萨夫·约维奇

博里萨夫·约维奇攝於2009年南斯拉夫社會主義聯邦共和國第12任總統任期1990年5月15日—1991年5月15日总理安特·马尔科维奇前任亚内兹·德尔诺夫舍克继任塞吉多·巴伊拉莫维奇（英语：Sejdo Bajramović）（代任）第12任不结盟运动秘书长任期1990年5月15日—1991年5月15日前任亚内兹·德尔诺夫舍克继任斯捷潘·梅西奇第3任塞尔维亚常驻南斯拉夫社会主义联邦共和国主席团代表任�...

Daniel J. Riordan

American politician For the voice actor, see Daniel Riordan. For the rugby player, see Daniel Riordan (rugby union). For the Wisconsin politician, see Daniel E. Riordan. Daniel J. Riordan Daniel Joseph Riordan (July 7, 1870 – April 28, 1923) was a U.S. Representative from New York for one term from 1899 to 1901 and for eight additional terms from 1906 to 1923. He was a Democrat and a member of Tammany Hall. Biography Riordan was born in New York City and attended public schools until 1886, ...

Jugantor

Bangladeshi daily newspaper This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jugantor – news · newspapers · books · scholar · JSTOR (February 2015) (Learn how and when to remove this message) Jugantor08 September 2023 front page of Bangladesh PratidinTypeDaily newspaperFormatBroadsheetEditorSaiful AlamFounded...

Brem

Indonesian traditional fermented food For the Soviet BREM series of armoured recovery vehicles, see Armoured recovery vehicle § Soviet Union/Russia. For other uses, see Brem (surname). BremSuling Mas brand Madiun bremPlace of originIndonesia Media: Brem Eagle brand Balinese brem Brem is traditional fermented food or fermented beverage from Indonesia. There are two types of brem, brem cake (solid) that is usually eaten as snack from Madiun and Wonogiri,[1] and brem beve...

Hinduism in Fiji

Overview of the presence and role of Hinduism in Fiji Hinduism by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Morocco Western Sahara Mozambique Namibia Niger Nigeria Rwanda São T...

لجنة الفصل في منازعات الأوراق المالية (السعودية)

لجنة الفصل في منارعات الأوراق المالية البلد السعودية المقر الرئيسي السعودية تاريخ التأسيس 1424هـ اللغات الرسمية العربية الرئيس سعود بن عبد الرحمن الشمري تعديل مصدري - تعديل لجنة الفصل في منازعات الأوراق المالية (السعودية) لجنة تختص بالفصل في المنازعات المالية، م...

Awliscombe

Village in Devon, England Human settlement in EnglandAwliscombeFarm buildings, AwliscombeAwliscombeLocation within DevonPopulation500 (2011)Civil parishAwliscombeShire countyDevonRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townHonitonPostcode districtEX14PoliceDevon and CornwallFireDevon and SomersetAmbulanceSouth Western UK ParliamentTiverton and Honiton List of places UK England Devon 50°49′00″N 3°14′00″W / 50.816667°N ...

Template talk:Abbasid caliphs

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to the following WikiProjects:Islam: Muslim history Islam portalThis template is within the scope of WikiProject Islam, a collaborative effort to improve the coverage of Islam-related articles on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.IslamWikipedia:WikiProject IslamTemplate:WikiProject IslamIslam-...

レベルデザイン

Edgeのレベルデザインレベルデザイン、環境デザイン[1]、は、ビデオゲームのレベル（ロケール、ステージまたはミッション）の作成に関するゲーム開発のー分野である[2] [3] [4] 。これは一般に、レベルを構築するために設計されたゲーム開発ソフトウェアであるレベルエディタ（英語版）を使用して行われる。レベル編集ツールが組み込まれて�...

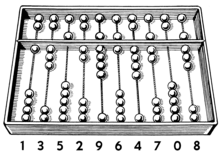
Abacus

Calculating tool Abaci redirects here. For the Turkish Surname, see Abacı. For the medieval book, see Liber Abaci. For other uses, see Abacus (disambiguation). Bi-quinary coded decimal-like abacus representing 1,352,964,708 An abacus (pl.: abaci or abacuses), also called a counting frame, is a hand-operated calculating tool which was used from ancient times in the ancient Near East, Europe, China, and Russia, until the adoption of the Arabic numeral system.[1] An abacus consists of a...

Cuba ai Giochi della XXVII Olimpiade

Cuba ai Giochi della XXVII OlimpiadeSydney 2000 Codice CIOCUB Comitato nazionaleComitato Olimpico Cubano Atleti partecipanti229 in 24 discipline Di cui uomini/donne147 - 82 PortabandieraFélix Savón Medagliere Posizione 9ª 11 11 7 29 Cronologia olimpica (sommario)Giochi olimpici estivi 1896 · 1900 · 1904 · 1908 · 1912 · 1920 · 1924 · 1928 · 1932 · 1936 · 1948 · 1952 · 1956 · 1960 · 1964 �...

Gruppo nilpotente

In matematica, un gruppo nilpotente è un gruppo G {\displaystyle G} che ammette una serie centrale, ovvero una successione di sottogruppi normali { 1 } ⊆ H 1 ⊆ H 2 ⊆ ⋯ ⊆ H n − 1 ⊆ H n = G {\displaystyle \{1\}\subseteq H_{1}\subseteq H_{2}\subseteq \cdots \subseteq H_{n-1}\subseteq H_{n}=G} tale che ogni quoziente H i + 1 / H i {\displaystyle H_{i+1}/H_{i}} è contenuto nel centro di G / H i {\displaystyle G/H_{i}} . Il minimo n {\displaystyle ...