Takata matsubara

Takata matsubara
Pemandangan hijau dekat tepi pantai
Takata matsubara sebelum tsunami Tohoku 2011.
Satu pohon pinus yang masih berdiri
Sebuah pohon pinus yang berdiri selamat di Takata matsubara sehabis tsunami Tohoku 2011. Pohon tersebut kemudian mati.

Takata matsubara (高田松原) adalah hutan pinus yang pernah ada di wilayah pesisir kota Rikuzentakata, Prefektur Iwate, Jepang, sebagai bagian dari Taman Nasional Rikuchu Kaigan.[1] Tempat ini sejak lama merupakan tempat wisata populer untuk dinikmati pemandangannya. Pada tanggal 11 Maret 2011, tsunami yang dipicu gempa bumi Sendai menghantam kota Rikuzentakata dan melenyapkan semua pinus di hutan ini, kecuali satu batang yang kemudian mati dan didirikan kembali di sana pada upacara peringatan tsunami tersebut.

Sejarah

Takata matsubara merupakan hutan pinus yang tumbuh di pesisir pantai sepanjang 2 km. Tempat ini telah dikenal akan keindahannya semenjak Zaman Edo (1603-1867).[2] Diperkirakan, sampai tahun 2011, usia pohon-pohon pinus Takata matsubara rata-rata telah mencapai 270-300 tahun.[2][3]

Takata matsubara yang merupakan bagian dari kawasan Taman Nasional Rikuchu Kaigan, terdiri dari 70.000 batang pohon jenis pinus hitam dan merah.[3] Pada tahun 1927 Takata matsubara dimasukkan dalam daftar "100 Pemandangan Terindah di Jepang" dan pada tahun 1940 dikategorikan sebagai "Tempat dengan Pemandangan Indah"[4] Selain, sebagai tempat wisata, Takata matsubara juga berfungsi sebagai penahan angin.

Pada tanggal 11 Maret 2011, tsunami setinggi 15 meter yang dipicu Gempa bumi dan tsunami Sendai 2011, menghantam kota Rikuzentakata dan melenyapkan seluruh pinus Takata matsubara. Rikuzentakata yang menjadi kota terparah yang diterjang tsunami, kehilangan 10% populasinya.

Kiseki no ippon matsu

Dari puluhan ribu batang pinus dan yang tersapu gelombang, tersisa satu pohon pinus yang masih berdiri sehingga dengan segera menjadi pusat perhatian.[5] Sebatang pinus setinggi 26,8 meter tersebut kemudian dinamakan "kiseki no ippon matsu" (sebatang pinus ajaib).[3] Namun, sistem akar dan daun pinus ini diketahui telah rusak akibat menyerap air laut.[5] Meskipun tim penyelamat telah dikerahkan untuk memompa air asin dan mempertahankan agar pinus itu bisa bertahan, kemampuan menyerap nutrisinya telah berkurang.[5] Penduduk ikut menyumbang untuk penyelamatan pinus tersebut. Pada tanggal 12 September 2012, pinus ini mati. Batangnya kemudian dibawa ke Laboratorium Biologi Yoshida, Kyoto untuk diawetkan sebelum untuk didirikan kembali sebagai monumen peringatan tsunami.[2] Batang dipotong menjadi beberapa bagian dan dibuatkan tulang dari metal.[6] Pada batang pinus dipasang replika ranting dan daun dari resin sintetik.[6] Pohon pinus ini didirikan kembali di Rikuzentakata pada upacara peringatan 2 tahun bencana tsunami pada tanggal 11 Maret 2013.[6]

Referensi

  1. ^ (Inggris)Introducing places of interest: Rikuchukaigan National Park Diarsipkan 2012-02-08 di Wayback Machine., Ministry of the Environment (Japan). 14-07-2013
  2. ^ a b c (Inggris)Tsunami 'miracle' pine tree was younger than thought Diarsipkan 2013-08-13 di Wayback Machine., Asahi Shimbun. 14-07-2013
  3. ^ a b c (Inggris)A Late Spring in Tōhoku (Part II), Nippon.com. 14-07-2013
  4. ^ (Inggris)Plans to spend £1.2 million saving Japan's 'miracle pine' under fire, Telegraph. 14-07-2013
  5. ^ a b c (Inggris)Sole surviving pine tree and symbol of Japan's post-tsunami hope is dying, Telegraph. 14-07-2013
  6. ^ a b c (Inggris)"Miracle Pine" Tree Reconstructed as a Memorial Sculpture to the Japanese Tsunami Diarsipkan 2014-11-14 di Wayback Machine., BLOUIN ARTINFO. 14-07-2013

Pranala luar

Read other articles:

I Marine Expeditionary Force

Military unit of the United States Marine Corps This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2018) (Learn how and when to remove this template message) I Marine Expeditionary ForceI MEF insigniaActive8 November 1969 – presentCountry United States of AmericaBranch United States Marine CorpsTypeMarine Air-Ground Task ForceRoleE...

 

 

Carrick mat

Flat woven decorative knot Carrick matCarrick mat made with three passesNamesCarrick mat, Prolong knotCategoryDecorativeRelatedCarrick bend, Turk's head, Austrian knotTypical useMat for padding or decorationABoK#2242, #2244Instructions[1] Carrick mats on schooner Adventuress, used to protect woodwork from the blocks when the lines are slack. 818 knotBasic seamless formArf invariant1Braid length8Braid no.3Bridge no.3Crosscap no.4Crossing no.8Genus3Hyperbolic volume12.35090621Unknotting no.2Con...

 

 

1970 في الهند

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 1970 في الهندمعلومات عامةالسنة 1970 1969 في الهند 1971 في الهند تعديل - تعديل مصدري - تعديل ويكي بيانات سنوات 1968: 196...

Ice Quake (film)

2010 television film directed by Paul Ziller This article is about the 2010 film Ice Quake. For the novel in the SOS adventure series novel Ice Quake see SOS Adventures. For information on factual Ice Quakes or Cryoseism see Cryoseism. Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (March 2017) (Learn how and when to remove this template message) Ice Q...

 

 

Omega Point

Idea that everything in the universe will converge to a final point of unification For other uses, see Omega Point (disambiguation). The Omega Point is a theorized future event in which the entirety of the universe spirals toward a final point of unification. The term was invented by the French Jesuit Catholic priest Pierre Teilhard de Chardin (1881–1955).[1] Teilhard argued that the Omega Point resembles the Christian Logos, namely Christ, who draws all things into himself, who in ...

 

 

Шалфей обыкновенный

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Cours universitaires de Davos

Cours universitaires de Davos mars 1928 Situation Création août 1927 Dissolution janvier 1933 Type Rencontres académiques Siège Davos Suisse Langue Français, Allemand, Anglais Organisation Dirigeant Gottfried Salomon Personnes clés Albert Einstein, Martin Heidegger, Léon Brunschvicg, Ernst Cassirer modifier  Les Cours universitaires de Davos, appelés Davoser Hochschulkurse en allemand, sont un projet de création d'une université internationale à Davos (Suisse, canton des Gris...

 

 

Campionato mondiale maschile di hockey su pista Lisbona 1949

Campionato del mondo 1949 Competizione Campionato del mondo Sport hockey su pista Edizione 5ª Organizzatore FIRS Date dal 28 maggioal 3 giugno 1949 Luogo  PortogalloLisbona Partecipanti 8 Risultati Vincitore Portogallo(3º titolo) Secondo Spagna Terzo Italia Quarto Belgio Statistiche Incontri disputati 28 Gol segnati 196 (7 per incontro) Cronologia della competizione 1948 1950 Manuale Il Campionato mondiale di hockey su pista 1949 (in inglese 1949 Roller Hockey World ...

 

 

Stadion Carlos Tartiere (1932)

Stadion Carlos TartiereNama lengkapStadion Carlos TartiereNama lamaStadion Buenavista (1932–1958)LokasiOviedo, SpanyolPemilikConcejo de OviedoOperatorReal OviedoKapasitas22.000 (1932–1982)23.500 (1982–1998)16.500 (1998–2003)PermukaanRumputKonstruksiDibuka24 April 1932Direnovasi1982Ditutup20 Mei 2000Dihancurkan2003ArsitekIldefonso Sánchez del RíoPemakaiReal Oviedo (1932–2000) Stadion Carlos Tartiere adalah sebuah stadion yang terletak di Oviedo, Spanyol. Stadion ini umumnya dipergu...

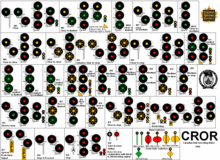
Canadian Rail Operating Rules

Railway operating rulebook This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2012) (Learn how and when to remove this message) The Canadian Rail Operating Rules is a set of operating rules for railways in Canada. It is used by every Canadian railway. Overview The Canadian Rail Operating Rules are intended to enhance railway safety. The rules cover emplo...

 

 

The Truth (1998 film)

1998 Indian filmThe TruthPosterDirected byShaji KailasWritten byS. N. SwamyProduced byAsharafStarringMammoottyThilakan Vani ViswanathMuraliJanardhananCinematographyAnandakuttanEdited byL. BhoominathanMusic byRajamaniProductioncompanyA. B. R. ProductionsRelease date 19 March 1998 (1998-03-19) Running time144 minutesCountryIndiaLanguageMalayalam The Truth is a 1998 Malayalam-language police procedural thriller film written by S. N. Swamy and directed by Shaji Kailas.[1] ...

 

 

Swan

Tribe of large water birds For other uses, see Swan (disambiguation). Cygnet redirects here. For other uses, see Cygnet (disambiguation). SwanTemporal range: Late Miocene – Holocene[1][2] PreꞒ Ꞓ O S D C P T J K Pg N Mute swans (Cygnus olor) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Anseriformes Family: Anatidae Subfamily: Anserinae Genus: CygnusGarsault, 1764 Type species Anas olor[3]Gmelin, 1789 Species 6 l...

Yukawa Institute for Theoretical Physics

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (April 2015) (Learn how and when to remove this message) The Yukawa Institute for Theoretical Physics (基礎物理学研究所, kiso butsurigaku kenkyūsho) is a research institute in the field of theoretical physics, attached to Kyoto University in Japan. It was inaugurated in...

 

 

Haiguangsi station

Metro station in Tianjin, China Haiguangsi海光寺General informationOther namesHaiguang TempleLocationNankai District, TianjinChinaOperated byTianjin Metro Co. Ltd.Line(s)     Line 1ConstructionStructure typeUnderground and ElevatedHistoryOpened12 June 2006Services Preceding station Tianjin Metro Following station Anshandaotowards Donggulu Line 1 Erweilutowards Liuyuan Haiguangsi Station (Chinese: 海光寺站), literally Haiguang Temple Station in English, is a...

 

 

Mead

Alcoholic beverage made from honey This article is about the alcoholic beverage. For other uses, see Mead (disambiguation). MeadSwedish elderflower-flavored mead.Typefermented beverageAlcohol by volume 3.5–20.5%Proof (US)7°–41°Colorpale yellowFlavordry, sweet or semi-sweetIngredientshoney, water, fruit, herbs, spicesVariantsmetheglyn, chouchen, bochetRelated productstej, midus, medovukha, bais, balché Mead (/miːd/), also called hydromel (particularly when low in alcohol content),...

Jacob Frey

Artikel ini bukan mengenai Jacob Frye. Jacob Frey Walikota Minneapolis Ke-48PetahanaMulai menjabat 2 Januari, 2018PendahuluBetsy HodgesPenggantiPetahanaAnggota dari Dewan Kota Minneapolisdari daerah ke-3Masa jabatan2 Januari, 2014 – 2 Januari, 2018PendahuluDiane HofstedePenggantiSteve Fletcher Informasi pribadiLahir23 Juli 1981 (umur 43)Oakton, Virginia, A.S.Partai politikDemocratic–Farmer–Labor PartySuami/istriMichelle Lilienthal ​ ​(m. 2010&#...

 

 

K3b

K3b Basisdaten Hauptentwickler Sebastian Trüg, Christian Kvasny, Michał Małek u. a. Entwickler KDE Aktuelle Version 24.05.0[1] (23. Mai 2024) Betriebssystem Linux/Unix Programmier­sprache C++ (Qt)[2] Kategorie CD-DVD-Brennprogramm Lizenz GNU GPL 2[2][3] deutschsprachig ja https://userbase.kde.org/K3b K3b ist ein unter Linux laufendes universelles Programm von KDE zur Behandlung optischer Datenmedien sowie Videos und Audios. Es wandelt gängig...

 

 

C. S. Golden House

Historic house in Alabama, United States United States historic placeC.S. Golden HouseU.S. National Register of Historic Places Show map of AlabamaShow map of the United StatesLocationThomaston, AlabamaCoordinates32°16′26″N 87°37′22″W / 32.27389°N 87.62278°W / 32.27389; -87.62278Built1898Architectural styleQueen AnneNRHP reference No.00001029[1]Added to NRHPAugust 31, 2000 The C.S. Golden House, also known as the Leonard and Ellie Cra...

Tangent bundle

Tangent spaces of a manifold Informally, the tangent bundle of a manifold (which in this case is a circle) is obtained by considering all the tangent spaces (top), and joining them together in a smooth and non-overlapping manner (bottom).[note 1] A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold M {\dis...

 

 

Equilateral triangle

Shape with three equal sides Equilateral redirects here. For other uses, see Equilateral (disambiguation). Equilateral triangleTypeRegular polygonEdges and vertices3Schläfli symbol{3}Coxeter–Dynkin diagramsSymmetry group D 3 {\displaystyle \mathrm {D} _{3}} Area 3 4 a 2 {\textstyle {\frac {\sqrt {3}}{4}}a^{2}} Internal angle (degrees)60° An equilateral triangle is a triangle in which all three sides have the same length, and three angles are equal. Because of these properties, the equilat...