Relasi Green
|
Read other articles:

Smallville Serie de televisión Logotipo de la serieCreado por Jerry SiegelJoe ShusterProtagonistas Tom Welling Kristin Kreuk Michael Rosenbaum Eric Johnson Sam Jones III Allison Mack Annette O'Toole John Schneider John Glover Jensen Ackles Erica Durance Aaron Ashmore Laura Vandervoort Cassidy Freeman Sam Witwer Justin Hartley Callum BlueIdioma(s) original(es) InglésN.º de temporadas 10N.º de episodios 217 (lista de episodios)ProducciónProductor(es) ejecutivo(s) Alfred GoughMiles MillarMi...

Discovering History in China PengarangPaul A. CohenNegaraA.S.BahasaInggrisSubjekHistoriografi TionghoaDiterbitkan1984; dicetak ulang 2010ISBNISBN 9780231151924 Discovering History in China: American Historical Writing on the Recent Chinese Past (terjemahan: Menemukan Sejarah di Tiongkok: Penulisan Sejarah Amerika mengenai Masa Lalu Tiongkok Saat Ini) adalah sebuah buku karya Paul A. Cohen yang memperkenalkan pemikiran-pemikiran di belakang sejarah-sejarah Amerika mengenai Tiongkok sejak tahun...

Untuk kelompok Bryophyta atau lumut dalam arti luas, lihat Lumut. Lumut daun Periode Karbon[1] – sekarang PreЄ Є O S D C P T J K Pg N Bryophyta Lumut daun di tanah dan dasar pohon di Allegheny National Forest, Pennsylvania, Amerika Serikat.TaksonomiSuperdomainBiotaSuperkerajaanEukaryotaKerajaanPlantaeSubkerajaanViridiplantaeInfrakerajaanStreptophytaSuperdivisiEmbryophytaDivisiBryophyta Schimper, 1879 Tata namaSinonim takson Musci L. Muscineae Bisch. Kelas[2] Takakiopsida S...

AliPoster rilis teatrikalSutradaraMichael MannProduserJon PetersMichael MannJames LassiterPaul ArdajiA. Kitman HoSkenarioMichael MannEric RothStephen J. RiveleChristopher WilkinsonCeritaGregory Allen HowardPemeranWill SmithJamie FoxxJon VoightMario Van PeeblesRon SilverJeffrey WrightMykelti WilliamsonJames ToneyPenata musikPieter BourkeLisa GerrardSinematograferEmmanuel LubezkiPenyuntingWilliam GoldenbergLynzee KlingmanStephen E. RivkinStuart WaksPerusahaanproduksiInitial Entertainment ...

Stratovolcano on the island of Honshu, Japan Mount Azumaya四阿山Highest pointElevation2,354 m (7,723 ft)Listing100 Famous Japanese MountainsCoordinates36°32′30″N 138°24′47″E / 36.54167°N 138.41306°E / 36.54167; 138.41306NamingEnglish translationarbour mountainLanguage of nameJapanesePronunciation[azumajasaɴ]GeographyMount AzumayaChubu region and Kantō region, Honshū, Japan GeologyMountain typeStratovolcanoClimbingEasiest routeHi...

Pour les articles homonymes, voir Monnaie (homonymie). La monnaie, commune mesure des échanges commerciaux : illustration de la théorie d'Aristote, édition de 1454-1455 d'après la traduction de Nicole Oresme. La monnaie est définie par Aristote par trois fonctions : unité de compte, réserve de valeur et intermédiaire des échanges. À la période contemporaine, cette définition ancienne persiste mais doit être amendée, entre autres par la suppression de toute référence...

Canadian retailer The T. Eaton Company LimitedTrade nameEaton'sCompany typePrivate (1869–1998)Public (1998–1999)IndustryRetail (department store)Founded1869FounderTimothy EatonDefunct1999 as a company2002 as a brandFateFiled for bankruptcy; assets were purchased by Sears Canada in 1999. Stores converted to Sears stores or shut down in 2002.SuccessorSears CanadaHeadquartersToronto, Ontario (with stores across Canada)Key peopleTimothy EatonJohn Craig EatonJohn David EatonNumber of employees...

Dalam artikel ini, nama keluarganya adalah Maulida, nama keluarga patronimik Jawa; Putri adalah nama keluarga matronimik Jawa, Raden Roro adalah gelar kehormatan bangsawan Jawa. Ayu Maulida PutriAyu berbicara sebagai Duta Dewan Perwakilan Rakyat Republik Indonesia, 2020LahirRaden Roro Ayu Maulida Putri11 Juli 1997 (umur 26)Surabaya, Jawa Timur, IndonesiaNama lainAyumaPendidikan SD Negeri Kaliasin III (2003–2009) SMP Negeri 1 Surabaya (2009–2012) SMA Trimurti (2012–2015) Fakult...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

TomistomaRentang fosil: Eosen - sekarang, 47.8–0 jtyl[1] PreЄ Є O S D C P T J K Pg N Tomistoma schlegelii Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Reptilia Ordo: Crocodilia Famili: Gavialidae Subfamili: Tomistominae Genus: TomistomaS. Müller, 1846 Spesies Tomistoma schlegelii Tomistoma cairense (punah) Tomistoma coppensi (punah) Tomistoma dowsoni (punah) Tomistoma lusitanicum (punah) Tomistoma adalah sebuah genus gavialidae. Mereka terk...

Halaman ini berisi artikel tentang produsen. Untuk lagu, lihat Mercedes Benz (lagu). Mercedes-BenzJenisDivisiIndustriOtomotifPendahulu Benz & Cie.(1883–1926) Daimler-Motoren-Gesellschaft(1890–1926) Didirikan28 Juni 1926; 97 tahun lalu (1926-06-28)Pendiri Karl Benz Gottlieb Daimler KantorpusatStuttgart, JermanWilayah operasiSeluruh duniaTokohkunciOla Källenius, Kepala Mercedes-Benz CarsProduk Mobil Truk Bus Mesin pembakaran dalam Mobil elektrik Kendaraan mewah Merek Mercedes-AMG ...
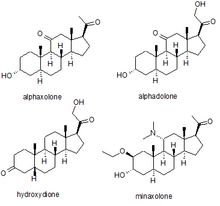
Compounds that affect neuronal excitability through modulation of specific ionotropic receptors Zuranolone, an example of a neurosteroid, used for the treatment of postpartum depression Neurosteroids, also known as neuroactive steroids, are endogenous or exogenous steroids that rapidly alter neuronal excitability through interaction with ligand-gated ion channels and other cell surface receptors.[1][2] The term neurosteroid was coined by the French physiologist Étienne-Émile...

Third Air ForceStemma della Third Air Force Descrizione generaleNazione Stati Uniti ServizioUnited States Air Force TipoNumbered air force ComandantiMaggior generaleJohn M. Wood Degni di notaLewis H. BreretonRoscoe C. WilsonFrancis H. Griswold Fonti indicate nel testo principale Voci su unità militari presenti su Wikipedia La Third Air Force (Air Forces Europe) (3 AF) è una numbered air force (NAF) delle United States Air Forces in Europe - Air Forces Africa (USAFE-AFAFRICA). Ha il qua...

New Zealand author (1924–2004) Janet FrameONZ CBEFrame in 1993BornJanet Paterson Frame(1924-08-28)28 August 1924Dunedin, New ZealandDied29 January 2004(2004-01-29) (aged 79)Dunedin, New ZealandOccupationNovelist, short story writer, essayist, poetLanguageEnglishGenreModernism, magic realism, postmodernismNotable worksAn Angel at My TableWebsitejanetframe.org.nz Janet Paterson Frame ONZ CBE (28 August 1924 – 29 January 2004) was a New Zealand author. She is internationally ren...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Part of a series on theCatholic Church by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Morocco Mozambique Namibia Niger Nigeria Rwanda São Tomé and Príncipe Senegal Seychelles S...

Sir Ludwig GuttmannLudwig GuttmannLahir(1899-07-03)3 Juli 1899Tost, Silesia Hulu, Prusia, Kekaisaran JermanMeninggal18 Maret 1980(1980-03-18) (umur 80)Aylesbury, Buckinghamshire, Britania RayaDikenal atasMembentuk Permainan ParalimpiadeProfesiNeurologisPenghargaanFellow of the Royal Society Sir Ludwig Poppa Guttmann CBE FRS[1] (3 Juli 1899 – 18 Maret 1980)[2][3] adalah seorang neurologis Inggris kelahiran Jerman[4] yang membentuk Perma...

Internal conflict in Ethiopia since 2018 OLA insurgencyPart of the Oromo conflict and Ethiopian civil conflict (2018–present)Map of Ethiopia showing the Oromia RegionDate6 August 2018 – presentLocationOromia Region, EthiopiaStatus OngoingStart of peace talks between government of Ethiopia and the OLA on 25 April 2023[1][2] Conflict resumes after peace talks failed in May 2023.Belligerents Ethiopia Oromia OLACommanders and leaders Abiy Ahmed Birhanu Jula Shimeli...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hungarian-Slovak Roma in the United States – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this message) Part of a series onRomani people Archaeology Cuisine Culture Dance Dress Folklore History Language Media Music ...

Former part of the Spanish Empire Map of the Spanish-Portuguese Empire in 1598. Territories administered by the Council of Castile Territories administered by the Council of Aragon Territories administered by the Council of Portugal Territories administered by the Council of Italy Territories administered by the Council of the Indies Territories appointed to the Council of Flanders The Council of Italy, officially, the Ro...














