ONE Championship

ONE Championship
OlahragaSeni bela diri campuran

Kickboxing

Muay Thai
Didirikan14 Juli 2011; 13 tahun lalu (2011-07-14)
PemilikGroup One Holdings Pte. Ltd.
CEOChatri Sityodtong (Chairman dan CEO)
Markas besarSingapore
Situs web resmihttp://www.onefc.com

ONE Championship (sebelumnya dikenal sebagai ONE Fighting Championship atau ONE FC) adalah promotor seni bela diri campuran (MMA), Muay Thai, dan kickboxing yang berbasis di Singapura yang diluncurkan pada tanggal 14 Juli 2011 oleh pengusaha Chatri Sityodtong dan mantan eksekutif senior ESPN Star Sports, Victor Cui.[1] ONE Championship didukung oleh Sequoia Capital, GIC, Temasek Holdings, Iconiq Capital, Mission Holdings, and Greenoaks Capital. Acara pertama promotor ini diadakan pada tanggal 3 September 2011 di Singapore Indoor Stadium; mereka telah mengadakan lebih dari 100 acara di seluruh wilayah Asia.[2]

ONE Championship secara luas dianggap sebagai properti media olahraga global terbesar di benuanya.[3][4] Atlet terkenal dalam daftarnya antara lain Demetrious Johnson, Eddie Alvarez, Nieky Holzken, Angela Lee, Aung La N Sang, Eduard Folayang, Giorgio Petrosyan, Roman Kryklia, Andrei Stoica, Bogdan Stoica, Tarik Khbabez, Regian Eersel, Yodsanklai Fairtex, Kevin Belingon, Bibiano Fernandes, Roger Gracie, Brandon Vera, Shinya Aoki, Xiong Jingnan, Vitor Belfort dan Ilias Ennahachi.

Lihat pula

Referensi

  1. ^ "ONE Fighting Championship™ unveils CHAMPION versus CHAMPION". sherdog.com. Diakses tanggal 18 August 2011. 
  2. ^ "EXCLUSIVE: ONE FC CEO Reveals Big Plans for China on Cusp of Beijing Debut". Yahoo!. Diakses tanggal 16 December 2014. 
  3. ^ Connolly, Matt. "Asia's Top Sports Media Properties: ONE, CSL, IPL and the Continent's Other Leaders". Forbes (dalam bahasa Inggris). Diakses tanggal 12 May 2020. 
  4. ^ "Billion dollar baby: The Asian MMA unicorn taking on the UFC". Nikkei Asian Review (dalam bahasa Inggris). Diakses tanggal 12 May 2020. 

Pranala luar

Ikon rintisan

Artikel bertopik perusahaan ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

Read other articles:

Whiteinch Victoria Park railway station

Former railway station in Scotland The site of the station in 2019 Whiteinch Victoria Park railway station was a suburban railway station serving Whiteinch in Glasgow, Scotland. It was opened as a goods station known as Whiteinch in 1874 as part of the newly constructed Whiteinch Railway. In 1897, the station was rebuilt as Whiteinch Victoria Park, with services running to Jordanhill railway station. Passenger services were suspended from 1 January 1917 until 2 June 1919.[1] Final clo...

 

 

Noh Sa-yeon

Ini adalah nama Korea; marganya adalah Noh. Noh Sa-yeonNoh Sa-yeon ketika bernyanyi dalam perayaan Hari KemerdekaanInformasi latar belakangNama lahir노사연Lahir3 Maret 1957 (umur 67)Changwon, Korea SelatanGenreK-popPekerjaanPenyanyi, Pembawa acaraTahun aktif1978 - sekarang Noh Sa-yeon (Hangul: 노사연; lahir 3 Maret 1957) adalah seorang penyanyi dan pembawa acara televisi asal Korea Selatan. Dia juga menjadi pembawa acara pada program radio 2 o'clock Manse dari tahun 2004 h...

 

 

Chang Hong

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Chang Hong (Hanzi sederhana: 苌弘; Hanzi tradisional: 萇弘, juga dikenal sebagai Hanzi sederhana: 苌宏; Hanzi tradisional: 萇宏, nama pemberian Shu Hanzi: 叔, 582? SM - 492 SM) merupakan seorang penduduk dari Zizhou di wila...

etena

Etena Nama Nama IUPAC Ethene Penanda Nomor CAS 74-85-1 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChEBI CHEBI:18153 Y ChEMBL ChEMBL117822 Y ChemSpider 6085 Y Nomor EC KEGG C06547 Y PubChem CID 6325 Nomor RTECS {{{value}}} UNII 91GW059KN7 Y CompTox Dashboard (EPA) DTXSID1026378 InChI InChI=1S/C2H4/c1-2/h1-2H2 YKey: VGGSQFUCUMXWEO-UHFFFAOYSA-N YInChI=1/C2H4/c1-2/h1-2H2Key: VGGSQFUCUMXWEO-UHFFFAOYAE SMILES C=C Sifat Rumus kimia C2H4&...

 

 

إنترناشيونال سوبر ستار سوكر (سلاسل)

  لمعانٍ أخرى، طالع إنترناشيونال سوبر ستار سوكر (توضيح). إنترناشيونال سوبر ستار سوكر غلاف اللعبة عام 1997. النوع كرة القدم المطور(ون) كونامي الناشر(ون) كونامي المِنصّة (أو المِنصّات) مايكروسوفت ويندوز  تاريخ الأصلي للإصدار 1995 أول إصدار إنترناشيونال سوبر ستار سوكر (13 نو�...

 

 

خط الفقر

نسبة الفقر العالمي عتبة الفقر أو خط الفقر (بالإنجليزية: poverty threshold)‏ أو (بالإنجليزية: poverty line)‏ هو أدنى مستوى من الدخل يحتاجه المرء أو الأسرة حتى يكون بالإمكان توفير مستوى معيشة ملائم في بلدٍ ما.[1][2][3] ومن هنا يظهر مصطلح الفقر المدقع (بالإنجليزية: absolute poverty)‏ وهو م�...

Loi de Lenz-Faraday

Pour les articles homonymes, voir Loi de Faraday. En physique, la loi de Lenz-Faraday, ou loi de Faraday, permet de rendre compte des phénomènes macroscopiques d'induction électromagnétique. Elle exprime l'apparition d'une force électromotrice (tension) dans un circuit électrique, lorsque celui-ci est immobile dans un champ magnétique variable ou lorsque le circuit est mobile dans un champ magnétique constant ou permanent. À l'origine empirique, cette loi est fondée sur les travaux...

 

 

Intel

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Masalah khususnya adalah: Kapitalisasi dan pemilihan diksi Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Intel di en.wikipedia.org. Isinya masih belum akurat, ...

 

 

The Principal's Office

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Principal's Office – news · newspapers · books · scholar · JSTOR (December 2023) (Learn how and when to remove this message) American TV series or program The Principal's OfficeGenreReality TVStarringJoey SussmanCountry of originUnited StatesNo. of seasons2No. of episodes21P...

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

 

 

Sophia Institute Press

American non-profit publishing company Crisis Magazine redirects here. For the NAACP publication, see The Crisis. This article reads like a press release or a news article and may be largely based on routine coverage. Please help improve this article and add independent sources. (March 2019) Sophia Institute PressStatusActiveFounded1983FounderJohn BargerSuccessorCharlie McKinney, PresidentCountry of originUnited StatesHeadquarters locationNashua, New HampshirePublication typesBooks, magazines...

 

 

Erula

Erula ÈrulaKomuneComune di ErulaLokasi Erula di Provinsi SassariNegaraItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaMarianna FuscoLuas • Total39,31 km2 (15,18 sq mi)Ketinggian457 m (1,499 ft)Populasi (2016) • Total745[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07030Kode area telepon079Situs webhttp://www.comunedierula.it Erula (bahasa Sardinia: Èrula) adalah sebuah k...

Outline of India

Overview of and topical guide to India The flag of IndiaThe Emblem of India An enlargeable map of the cities of IndiaThe following outline is provided as an overview of, and topical guide to, India: The seventh-largest country by area, India is located on the Indian subcontinent in South Asia. India was home to the ancient Indus Valley civilisation, and is the birthplace of four world religions: Hinduism, Sikhism, Buddhism, Jainism. India endured colonisation, eventually being administer...

 

 

Sydney Yugoslav General Trade and Tourist Agency bombing

Terror attack in 1972 in Sydney, Australia Part of a series onTerrorism in Australia Notable attacks Sydney Yugoslav General Trade and Tourist Agency bombing (1972) Sydney Hilton bombing (1978) Sydney Israeli consulate and Hakoah Club bombings (1982) Russell Street bombing (1986) Turkish consulate bombing (1986) French consulate bombing (1995) Endeavour Hills stabbings (2014) Lindt Cafe siege (2014) Parramatta shooting (2015) Queanbeyan stabbing attacks (2017) Brighton siege (2017) Mill Park ...

 

 

Electoral district of Fuller

Former state electoral district of New South Wales, Australia Fuller was an electoral district of the Legislative Assembly in the Australian state of New South Wales, created in 1968 in the Ryde area and named after George Fuller, Premier of New South Wales, 1922–1925. It was abolished in 1981 and largely replaced by Gladesville.[1][2][3][4] Members for Fuller Member Party Period   Peter Coleman Liberal 1968–1978   Rodney Cavalier Labor 1978–198...

The Story of Abraham (tapestries)

The Story of AbrahamArtistAttributed to Pieter van Aelst IIIYear1540 - 1543TypeTapestryDimensions482.0 cm × 770.0 cm (189.76 in × 303.15 in)LocationHampton Court Palace, Richmond upon Thames, Greater LondonUnited Kingdom The Story of Abraham is a set of ten Brussels tapestries depicting stories from the life of the biblical prophet Abraham. They appear to have been designed by Bernaert van Orley initially, but completed by Pieter Coecke van Aelst ar...

 

 

سعد الجوهر

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) سعد الجوهر معلومات شخصية الميلاد 1365هـالخرج تاريخ الوفاة 1424هـ الطول 176 سم مركز اللعب دفاع الجنسية السعودية&#...

 

 

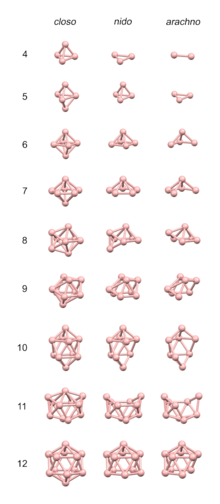
Polyhedral skeletal electron pair theory

Electron counting rules In chemistry the polyhedral skeletal electron pair theory (PSEPT) provides electron counting rules useful for predicting the structures of clusters such as borane and carborane clusters. The electron counting rules were originally formulated by Kenneth Wade,[1] and were further developed by others including Michael Mingos;[2] they are sometimes known as Wade's rules or the Wade–Mingos rules.[3] The rules are based on a molecular orbital treatm...

Paradox

Statement that apparently contradicts itself For other uses, see Paradox (disambiguation). A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation.[1][2] It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion.[3][4] A paradox usually involves contradictory-yet-interrelated elements that ex...

 

 

Sjöfart

Ångfartyget Madagascar Sjöfart är framförandet av fartyg till sjöss. Oftast transporterar fartygen gods och passagerare men några andra syften med sjöfart är krigföring, forskning och fiske. Cirka 90 % av alla godstransporter sker sjövägen. I begreppet sjöfart räknas även konstruktion och reparation av fartyg, hamn- och farledsverksamhet, skeppsmäkleri, godstransport till och från hamnarna samt försäkring av gods, fartyg och människor ombord. I Sverige är Transportsty...