Keragaman topologi
|
Read other articles:

Bukit Santo Tomas பரங்கி மலைParangimalaiHillockBukit Santo TomasTampilkan peta ChennaiBukit Santo TomasTampilkan peta Tamil NaduBukit Santo TomasTampilkan peta IndiaKoordinat: 13°0′18.2″N 80°11′35.9″E / 13.005056°N 80.193306°E / 13.005056; 80.193306Koordinat: 13°0′18.2″N 80°11′35.9″E / 13.005056°N 80.193306°E / 13.005056; 80.193306NegaraIndiaNegara bagianTamil NaduMetroChennaiKetinggian91,44 m (30,0...

مسجد مصطفى محمود معلومات عامة القرية أو المدينة الجيزة الدولة مصر تاريخ بدء البناء 1979 ويكيميديا كومنز مسجد مصطفى محمود تعديل مصدري - تعديل مسجد مصطفى محمود أو مسجد محمود -التسمية الصحيحة للمسجد- بناه العالِم الموسوعي والأديب والمفكر المصري د.مصطفى محمود في عام 1979م. يقع...

Struggle of a religious kind in Islam For other uses, see Jihad (disambiguation). Part of a series onIslamic jurisprudence(fiqh) Ritual Shahada Salah Raka'ah Qibla Turbah Sunnah prayer (TahajjudTarawih) Witr Nafl prayer Sawm Zakat Hajj Ihram (clothing Mut'ah) Tawaf Umrah (and Hajj) Political Islamic leadership Caliphate Majlis-ash-Shura Imamate Wilayat al-faqih Bay'ah Dhimmi Aman Family Marriage Contract Mahr Misyar Halala Urfi Mut‘ah Polygyny Divorce Khula Zihar Iddah Kafa'ah Ado...

Choice Hotels InternationalJenisPublik (NYSE: CHH)IndustriPenginapanDidirikan1939Kantorpusat Silver Spring, MarylandCabang 5.500Wilayah operasiInternasionalProdukQuality Inn®Choice Hotels®Cambria Suites®Comfort Inn®Comfort Suites®Quality®Sleep Inn®Clarion®MainStay Suites®Suburban Extended Stay Hotel®Econo Lodge®Rodeway Inn®IndukChoice Hotels InternationalSitus webwww.Choicehotels.com Choice Hotels International adalah jaringan penginapan waralaba berkantor pusat di Silver Spring, ...

Astrakhan kotakota besarwilayah administratifpelabuhan Астрахань (ru) flags of Astrakhan (en) Tempat Negara berdaulatRusiaOblast di RusiaOblast AstrakhanUrban okrug in Russia (en)Astrakhan Urban Okrug (en) Ibu kota dariOblast Astrakhan Astrakhan Urban Okrug (en) Astrakhan Governorate (en) Astrakhan Okrug (en) (1928–1930)Astrakhan Okrug (en) (1937–1943)Caucasus Viceroyalty (en) (1790–1796) NegaraRusia Pembagian administratifLeninsky District (en) Kirovsky City Distri...

Aboriginal people from Goa, India This article is about the Gauda and Kunbi communities in Goa. For other groups labeled Kunbi, see Kunbi (disambiguation). Gaudas are aboriginal people residing in the coastal Indian state of Goa. They are believed to be the original inhabitants of Konkan. Most follow folk Hinduism, but many were converted to Catholicism by the Portuguese missionaries during the Christianisation of Goa while still keeping their folk tradition and culture alive.[1] Kunb...

Donkey Kong 64 PublikasiNA: 22 November 1999[2]PAL: 6 Desember 1999[1]JP: 10 Desember 1999GenrePlatform, adventureKarakterDonkey Kong (karakter), Diddy Kong, Lanky Kong (en), Chunky Kong (en) dan Tiny Kong (en) Latar tempatDonkey Kong universe (en) Karakteristik teknisPlatformNintendo 64 Modepermainan video multipemain dan Permainan video pemain tunggal FormatROM cartridge dan unduhan digital Metode inputNintendo 64 controller (en) Format kode Daftar 30 Informasi pengembangPen...

Niklaus Riser Landamano di NidvaldoDurata mandato1609-1610, 1615-1616 Commissario a BellinzonaDurata mandato1576 –1577 Usciere di NidvaldoDurata mandato1572 –1575 Dati generaliSuffisso onorificoRitter Professioneimprenditore e militare Niklaus Riser (Dallenwil, 1539 o 1540 – Oberdorf, 1º aprile 1632) è stato un imprenditore, politico e militare svizzero di religione cattolica.[1] Indice 1 Biografia 2 Note 3 Bibliografia 4 Collegamenti este...

« Thatcher » redirige ici. Pour les autres significations, voir Thatcher (homonymie). Pour les articles homonymes, voir Dame de fer. Margaret Thatcher Margaret Thatcher au milieu des années 1990. Fonctions Première ministre du Royaume-Uni 4 mai 1979 – 28 novembre 1990(11 ans, 6 mois et 24 jours) Monarque Élisabeth II Vice-Premier ministre William Stephen Whitelaw (1979-1988)Geoffrey Howe (1989-1990) Gouvernement Thatcher I, II et III Législature 48e, 49e et 5...

Protected area in the Northern Territory, AustraliaCorroboree Rock Conservation ReserveNorthern TerritoryIUCN category V (protected landscape/seascape)[1] Corroboree RockCorroboree Rock Conservation ReserveCoordinates23°40′52″S 134°12′57″E / 23.68111°S 134.21583°E / -23.68111; 134.21583Established1962[1]Area7 hectares (17 acres)[1]Visitation15,000 (in 2011)[2]Managing authoritiesParks and Wildlife Commission of the Nort...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Mais Linhas AéreasDidirikan2010Armada2Situs webwww.voemais.com.br Mais Linhas Aéreas adalah maskapai penerbangan Brasil yang didirikan pada tahun 2010. Sejarah Mais Linhas Aéreas didirikan pada 2010 dan diharapkan mulai beroperasi pada Desember 2011. ...

Radio station in Fremont, NebraskaKHUBFremont, NebraskaBroadcast areaFremont, NebraskaFrequency1340 kHzBrandingThe Big DogProgrammingFormatCountryAffiliationsABC Radio, Salem Communications, Westwood OneOwnershipOwnerSteven W. Seline(Walnut Radio, LLC)Sister stationsKFMTHistoryFirst air dateDecember 22, 1939[1]Former call signsKORN (1939–1949)KFGT (1949–1958)Technical informationFacility ID34550ClassCPower500 watts (day)250 watts (night)Transmitter coordinates41°25′58.00″N 96...

Major League Baseball season Major League Baseball team season 2005 Chicago White SoxWorld Series ChampionAmerican League ChampionAmerican League Central Division ChampionLeagueAmerican LeagueDivisionCentralBallparkU.S. Cellular FieldCityChicagoRecord99–63 (.611)Divisional place1stOwnersJerry ReinsdorfGeneral managersKenny WilliamsManagersOzzie GuillénTelevisionWGN-TVComcast Sportsnet(Ken Harrelson, Darrin Jackson)RadioWMVP(John Rooney, Ed Farmer)WRTO (AM)(Hector Molina) ← ...

Sporting event delegationAntigua and Barbuda at theParalympicsIPC codeANTNPCAntigua and Barbuda Paralympic CommitteeMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer appearances2012201620202024 Antigua and Barbuda made its Paralympic Games début at the 2012 Summer Paralympics in London,[1] sending a single representative (Jamol Pilgrim) to compete in athletics. The Antigua and Barbuda Paralympic Committee (ABPC) was established on 15 March 2012. Its immediate purpose was to enable Pilgr...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2021) جغرافية جزر بيتكيرنمعلومات عامةالقارة جزيرة أوقيانوسيا الأرض والتضاريسالمساحة 47 كم² تعديل - تعديل مصدري - تعديل ويكي بيانات خريطة جزر بيتكيرن. جغرافيا جزر بي...

القانون المؤسسي رقم خمسةمعلومات عامةالبداية 13 ديسمبر 1968 البلد البرازيل[1] الاختصاص حكومة البرازيل الاتحادية[1] مكان النَّشر برازيليا[1] لغة العمل أو لغة الاسم برتغالية برازيلية[1] تاريخ النشر 13 ديسمبر 1968[1] عدد الصفحات 9 المجموعة الأرشيف الوطني العمل الك�...
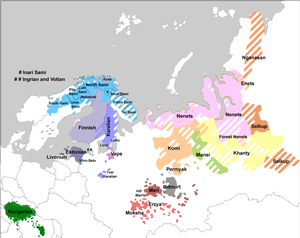
Samoyedic languages spoken in Russia Not to be confused with Enets language. Nenetsненэцяʼ вадаnenécja' vadaNative toRussiaRegionNenets Autonomous Okrug, Yamalo-Nenets Autonomous Okrug, Krasnoyarsk Krai, Komi Republic, Murmansk Oblast[citation needed]Ethnicity49,787 (2020 census)[1]Native speakers38,405 (2020 census)[2]Language familyUralic Samoyedic(core)Enets–NenetsNenetsDialects Forest Nenets Tundra Nenets Language codesISO 639-3yrkGlottologn...

1999 horror film From Dusk Till Dawn 3:The Hangman's DaughterPoster for From Dusk Till Dawn 3: The Hangman's DaughterDirected byP. J. PesceScreenplay byÁlvaro RodríguezStory by Álvaro Rodríguez Robert Rodríguez Produced by Michael S. Murphey Gianni Nunnari Meir Teper Starring Marco Leonardi Michael Parks Rebecca Gayheart Lennie Loftin Ara Celi Jordana Spiro Orlando Jones Danny Trejo Temuera Morrison Sônia Braga CinematographyMichael BonvillainEdited byLawrence A. MaddoxMusic byNathan Ba...

Central Flying SchoolA North American Harvard, the school's previously used aircraft.Active1932 - PresentCountryBranchSouth African Air ForceRoleab initio flight training school.Size20 Instructors, 50 Students per annumCurrent BaseAFB Langebaanweg, LangebaanMotto(s)Facta Nostra Vivent (Our Deeds Shall Live)[1][2]AnniversariesFirst formed: 1932 (at Zwartkop Air Station)[3]Current AircraftPilatus PC-7 MkII[4]Aircraft flownBomberPreviously Flown de Havilland DH.9...

Peñón de Ifach Penyal d'Ifac Categoría UICN VI (área protegidade recursos gestionados) SituaciónPaís EspañaComunidad Comunidad ValencianaProvincia AlicanteCoordenadas 38°38′05″N 0°04′28″E / 38.63472222, 0.07444444Datos generalesAdministración Generalidad ValencianaGrado de protección Parque naturalFecha de creación 19 de enero de 1987Legislación Decreto 1/1987N.º de localidades 1 municipioCalpe Superficie 53,3 ha Peñón de I...