Read other articles:

Dolichoprosopus Dolichoprosopus lethalis Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Dolichoprosopus Dolichoprosopus adalah genus kumbang tanduk panjang yang tergolong famili Cerambycidae. Genus ini juga merupakan bagian dari ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang dalam genus ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu hidup atau kayu...
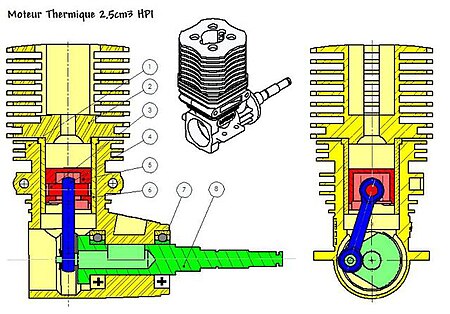
Motore dell'Aprilia RS 125 R, con un primo piano del carburatore e della valvola rotante classica Il sistema di ammissione a disco rotante (anche detto con valvola a disco rotante) è un tipo di alimentazione e distribuzione per il motore a due tempi. Tra i diversi sistemi d'ammissione risulta essere il più adatto per le competizioni. Indice 1 Storia 2 Descrizione 2.1 Classiche 2.2 Accorgimenti 3 Svantaggi 4 Vantaggi 5 Note 6 Voci correlate 7 Collegamenti esterni Storia L'ideazione dei motor...

Connie SutedjaConnie di Madjalah Aktuil Edisi 37 Tahun 1969LahirSukarni10 November 1944 (umur 79)Tasikmalaya, Masa Pendudukan JepangNama lainConnie SutedjaPekerjaanPemeranmodelTahun aktif1965—sekarangAnak1 Sukarni binti Sutedja (lahir 10 November 1944), lebih dikenal sebagai Connie Sutedja[1] adalah pemeran dan model Indonesia. Ia merupakan salah satu dari empat anggota Golden Girls bersama Nani Widjaja, Ida Kusumah dan Rina Hassim. Pada awal karirnya sebagai pemain ...

Родосский треугольникангл. Triangle at Rhodes Публикация рассказа в журнале Strand Magazine, 1936 Жанр рассказ Автор Агата Кристи Язык оригинала английский Дата написания 1936 Дата первой публикации 1937 Издательство Collins Crime Club «Родосский треугольник» (англ. Triangle at Rhodes)[К 1] — детек�...

Artikel ini memberikan informasi dasar tentang topik kesehatan. Informasi dalam artikel ini hanya boleh digunakan untuk penjelasan ilmiah; bukan untuk diagnosis diri dan tidak dapat menggantikan diagnosis medis. Wikipedia tidak memberikan konsultasi medis. Jika Anda perlu bantuan atau hendak berobat, berkonsultasilah dengan tenaga kesehatan profesional. JerawatSebuah ilustrasi jerawatInformasi umumSpesialisasiDermatologi, Kedokteran keluarga Jerawat adalah suatu penyakit kulit yang cuku...

American silent film and stage actress (1857-1937) For the female soloist pop star, see Leslie Carter. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mrs. Leslie Carter – news · newspapers · books · scholar · JSTOR (June 2020) (Learn how and when to remove this template message) Mrs. Leslie CarterMrs. Lesli...

Railway station in Motosu, Gifu Prefecture, Japan Hinata Station日当駅Hinata Station in May 2005General informationLocationHinata, Motosu-shi, Gifu-ken 501-1231JapanCoordinates35°34′56.48″N 136°37′53.09″E / 35.5823556°N 136.6314139°E / 35.5823556; 136.6314139Operated by Tarumi RailwayLine(s)■ Tarumi LineDistance28.3 km from ŌgakiPlatforms1 side platformTracks1Other informationStatusUnstaffedWebsiteOfficial website (in Japanese)HistoryOpenedMarch 25, 1...

Adolfo Bielli Nazionalità Argentina Calcio Ruolo Attaccante Carriera Squadre di club1 1961 Boca Juniors1 (0)1962-1964 Estudiantes67 (19)1965-1968 Rosario Central90 (22) Nazionale 1964 Argentina5 (1) Palmarès Taça das Nações Oro Brasile 1964 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Adolfo Alberto Bielli (Buenos Air...

Joona Toivio Nazionalità Finlandia Altezza 183 cm Peso 80 kg Calcio Ruolo Difensore Squadra HJK Carriera Giovanili HJK2007-2008 AZ Alkmaar Squadre di club1 2008-2010→ Telstar47 (0)2010-2012 Djurgården86 (9)2013-2017 Molde89 (12)2018 Nieciecza9 (1)2018-2021 Häcken95 (4)2022- HJK0 (0) Nazionale 2008-2009 Finlandia U-2110 (0)2009-2021 Finlandia78 (3) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionat...

Министерство природных ресурсов и экологии Российской Федерациисокращённо: Минприроды России Общая информация Страна Россия Юрисдикция Россия Дата создания 12 мая 2008 Предшественники Министерство природных ресурсов Российской Федерации (1996—1998)Министерство охраны...

Thomas PesquetPesquet nel 2016Astronauta dell'ESANazionalità Francia StatusIn attività Data di nascita27 febbraio 1978 Selezione2009 (Gruppo ESA 3) Primo lancio17 novembre 2016 Ultimo atterraggio9 novembre 2021 Altre attivitàIngegnere Tempo nello spazio396 giorni, 11 ore e 34 minuti Numero EVA6 Durata EVA39 ore 54 min Missioni Sojuz MS-03 SpaceX Crew-2 Modifica dati su Wikidata · Manuale Thomas Pesquet (Rouen, 27 febbraio 1978) è un ingegnere, aviatore e astronauta francese del...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Ashland Daily TidingsTypeDaily newspaperFormatTabloidOwner(s)Rosebud MediaFounded1876Ceased publicationAug. 1, 2021Circulation< 2,000 (Monday through Saturday)Websitedailytidings.com The Ashland Daily Tidings was a afternoon newspaper serving the city of Ashland, Oregon, United States. It was owned and published by Edd Rountree from 1960-1985 when he retired and subsequently purchased by Medford-based Mail Tribune, which it continued to publish until announcing that paper would close on Ja...

Protein-coding gene in the species Homo sapiens This article is about the enzyme. For the OAuth security extension PKCE, see OAuth § Security_issues. PRKCEAvailable structuresPDBOrtholog search: PDBe RCSB List of PDB id codes2WH0IdentifiersAliasesPRKCE, PKCE, nPKC-epsilon, protein kinase C epsilonExternal IDsOMIM: 176975; MGI: 97599; HomoloGene: 48343; GeneCards: PRKCE; OMA:PRKCE - orthologsGene location (Human)Chr.Chromosome 2 (human)[1]Band2p21Start45,651,345 bp[1]End4...

French statesman (1619–1683) For his son, see Jean-Baptiste Colbert, Marquis de Seignelay. Jean-Baptiste ColbertLord of Vandières and CernayPortrait de Jean-Baptiste Colbert (1655)by Philippe de ChampaigneFirst Minister of StateIn office9 March 1661 – 6 September 1683MonarchLouis XIVPreceded byJules Raymond MazarinSucceeded byThe Marquis of LouvoisSecretary of State of the NavyIn office7 March 1669 – 6 September 1683MonarchLouis XIVPreceded byThe Marquis of FresnesSuc...

Prefecture-level city in Anhui, People's Republic of China Not to be confused with Huai'an. For other uses, see Huainan (disambiguation). You can help expand this article with text translated from the corresponding article in Chinese. (June 2020) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, ...

American magazine Not to be confused with Life (journal). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Life magazine – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this message) LifeA cover of Life magazine in 1911EditorGeorge Cary EgglestonFormer editorsRober...

County in Nebraska, United States County in NebraskaHamilton CountyCountyHamilton County courthouse in AuroraLocation within the U.S. state of NebraskaNebraska's location within the U.S.Coordinates: 40°53′N 98°01′W / 40.88°N 98.02°W / 40.88; -98.02Country United StatesState NebraskaFounded1867 (created)1870 (organized)Named forAlexander HamiltonSeatAuroraLargest cityAuroraArea • Total547 sq mi (1,420 km2) • Land5...
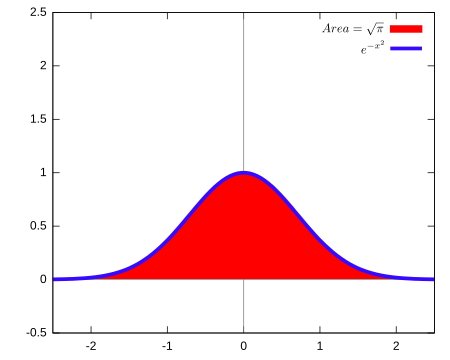
Grafik dari fungsi f(x) = e−x2 dan luas di antara fungsi tersebut dan sumbu x (yakni, di sepanjang garis), sama dengan π {\displaystyle \scriptstyle {\sqrt {\pi }}} . Integral Gauss, juga dikenal dengan nama integral Euler–Poisson, merupakan integral dari fungsi Gauss e−x2 di sepanjang garis real. Integral ini dinamai dari matematikawan Jerman Carl Friedrich Gauss, yang dirumuskan sebagai ∫ − ∞ ∞ e − x 2 d x = π {\displaystyle \int _...

Pattern of activity often with a result Wikimedia developer workflow An IMRAD model for developing research articles Workflow is a generic term for orchestrated and repeatable patterns of activity, enabled by the systematic organization of resources into processes that transform materials, provide services, or process information.[1] It can be depicted as a sequence of operations, the work of a person or group,[2] the work of an organization of staff, or one or more simple or ...