Himpunan lonjong
|
Read other articles:
Édouard Estaunié(1923) Nama dalam bahasa asli(fr) Édouard Estaunié BiografiKelahiran4 Februari 1862 Dijon Kematian2 April 1942 (80 tahun)Paris 57è President of the Société des gens de lettres (en) 1926 – 1929 ← Georges Lecomte (en) – Pierre Benoît (en) → 17è Seat 24 of the Académie française (en) 15 November 1923 – 2 April 1942 ← Alfred Capus – Louis-Pasteur Vallery-Radot (en) → Data priba...

Measure of the spread of light in an optical system Conservation of etendue Etendue or étendue (/ˌeɪtɒnˈduː/; French pronunciation: [etɑ̃dy]) is a property of light in an optical system, which characterizes how spread out the light is in area and angle. It corresponds to the beam parameter product (BPP) in Gaussian beam optics. Other names for etendue include acceptance, throughput, light grasp, light-gathering power, optical extent,[1] and the AΩ product. Through...

Bahasa Sunda Banyumas Badéolan PengucapanbadɛjɔlanWilayahKabupaten BanyumasKepunahan1980-an Rumpun bahasaAustronesia Melayu-PolinesiaKalimantan Utara Raya?Sunda-BaduiSunda Banyumas Kode bahasaISO 639-3–GlottologTidak adaQIDQ56197452 Status konservasi Punah EXSingkatan dari Extinct (Punah)Terancam CRSingkatan dari Critically endangered (Terancam Kritis) SESingkatan dari Severely endangered (Terancam berat) DESingkatan dari Devinitely endangered (Terancam) VUSingkatan dari Vulnerable (Rent...

Armor Holdings, Inc.Company typeSubsidiaryIndustryDefenseFoundedJanuary 1, 1996HeadquartersJacksonville, Florida, United StatesOwnerBAE SystemsParentBAE Systems Land and ArmamentsDivisionsacquired vehicle division of Stewart & StevensonWebsitewww.armorholdings.com Armor Holdings, Inc. was an American manufacturer of military, law enforcement, and personnel safety equipment. It was acquired by BAE Systems on July 31, 2007[1] and renamed BAE Systems Mobility & Protection Systems...

19th-century American slave trader Robert H. ElamNotice, Natchez Daily Courier, February 10, 1852Bornc. 1820TennesseeDiedafter 1864UnknownOther namesR. H. ElamOccupationSlave traderYears active1845?–1864 Robert H. Elam (c. 1820 – after 1864), usually advertising as R. H. Elam, was an American interstate slave trader who worked in Tennessee, Kentucky, Louisiana, and Mississippi. Biography Elam was born about 1820 in Tennessee.[1] According to a 19...

Colonial head of the Gilbert and Ellice Islands civil service (1892–1979) Governor of the Gilbert and Ellice IslandsFlag from 1937 to 1976StyleHis ExcellencyResidenceGovernment House, BairikiAppointerQueen Elizabeth IIas Queen of the United KingdomTerm lengthAt Her Majesty's pleasurePrecursorResident CommissionerFormation1 January 1972First holderJohn FieldFinal holderReginald James WallaceAbolished12 July 1979 The Presidential residence, former Government House, Bairiki. The Governor of th...

Questa voce o sezione sull'argomento società calcistiche italiane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. A.C. Ponte San PietroCalcio Ponte, Blues Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Bianco, blu Simboli Ponte Dati societari Città Ponte San Pietro Nazione Italia Confederazione UEFA Federazione FIGC Campionato Se...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Santiago Vergini Informasi pribadiNama lengkap Santiago Vergini[1]Tanggal lahir 3 Agustus 1988 (umur 35)Tempat lahir Rosario, ArgentinaTinggi 1,91 m (6 ft 3 in)Posisi bermain BekInformasi klubKlub saat ini Boca JuniorsNomor ...

Autoritratto (ca. 1907) Claudio Castelucho y Diana (Barcellona, 5 luglio 1870 – Parigi, 31 ottobre 1927) è stato un pittore spagnolo. Indice 1 Biografia 2 Note 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Biografia Il padre di Claudio Castelucho era Antoni Castelucho Vendrell, ed era uno scenografo. Claudio ricevette da lui le prime lezioni, e collaborò anche a diversi trattati artistici di teoria della prospettiva. Tenne le sue mostre quando era poco più che adolescente.[1...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Министерство природных ресурсов и экологии Российской Федерациисокращённо: Минприроды России Общая информация Страна Россия Юрисдикция Россия Дата создания 12 мая 2008 Предшественники Министерство природных ресурсов Российской Федерации (1996—1998)Министерство охраны...

Pour les articles homonymes, voir Autoportrait (homonymie). AutoportraitArtiste RembrandtDate Vers 1652Type Huile sur toileTechnique PeintureDimensions (H × L) 112 × 81 cmSérie Autoportraits de RembrandtMouvement Âge d'or de la peinture néerlandaiseNo d’inventaire GG_411Localisation Musée d'Histoire de l'art de Vienne, Vienne (Autriche)Coordonnées 48° 12′ 13″ N, 16° 21′ 41″ ELocalisation sur la carte d’AutricheLo...

المنتقمون: الحرب اللانهائيةAvengers: Infinity War (بالإنجليزية)[1] الشعارالملصق الدعائي للفيلممعلومات عامةالصنف الفني فيلم بطل خارق — فيلم خيال علمي[2] — فيلم أكشن[2] — فيلم مغامرة[2] الموضوع إبادة جماعية تاريخ الصدور 25 أبريل 2018[3] (فرنسا، الدنمارك، إيطاليا)26 أ�...

Language of Oaxaca, Mexico Not to be confused with the Hoava language of the Solomon Islands. HuaveOmbeayiiüts, UmbeyajtsNative toMexicoRegionOaxacaEthnicityHuave peopleNative speakers20,000 (2020 census)[1]Language familyLanguage isolateDialects Eastern (San Dionisio and San Francisco del Mar) Western (San Mateo and Santa Maria del Mar) Language codesISO 639-3Variously:hue – San Francisco del Marhuv – San Mateo del Marhve – San Dionisio ...
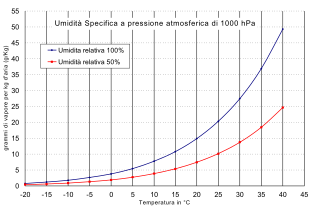
L'umidità è la quantità d'acqua o di vapore acqueo contenuta nell'atmosfera (o, più in generale, in una massa d'aria), in una sostanza o in un corpo[1]. Clima umido proprio delle foreste pluviali. Indice 1 Parametri di umidità 2 Umidità di saturazione 3 Umidità atmosferica 3.1 Effetti visibili dell'umidità atmosferica 3.2 Classificazione delle zone climatiche 4 Umidità del terreno 5 Umidità negli edifici 6 Strumenti di misura 7 Note 8 Voci correlate 9 Altri progetti 10 Colle...

Travel show hosted by Conan O'Brien Conan O'Brien Must GoTitle card for the showGenreComedyTravel showCreated byConan O'BrienDirected byMike SweeneyPresented byConan O'BrienOriginal languageEnglishNo. of seasons1No. of episodes4ProductionExecutive producersConan O'BrienJeff RossProduction companyConacoOriginal releaseNetworkMaxReleaseApril 18, 2024 (2024-04-18) –present (present)Related Conan Conan Without Borders Conan O'Brien Needs a Friend Conan O'Brien Must Go is a travel...

عبد العزيز المطهري وزير المالية التونسي في المنصب26 ديسمبر 1977 – 25 أبريل 1980 (سنتان و3 أشهرٍ و30 يومًا) الرئيس الحبيب بورقيبة الحكومة نويرة رئيس الوزراء الهادي نويرة محمد الفيتوري منصور معلى معلومات شخصية تاريخ الميلاد 27 نوفمبر 1922(1922-11-27) الوفاة 20 مايو 2004 (81 سنة)تونس العاصمة الج...

State integrated, boys, secondary school in Central Hawke's Bay, New ZealandTe Aute CollegeAddress100 State Highway 2PukehouCentral Hawke's Bay 4142New ZealandCoordinates39°49′38″S 176°38′04″E / 39.8273°S 176.6345°E / -39.8273; 176.6345InformationTypeState Integrated, Boys, SecondaryMottoWhakatangata Kia KahaQuit ye like men – be strongEstablished1854Ministry of Education Institution no.232PrincipalRachel Kingi (acting)School roll82[2] (Febr...

UK phone retailer This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dial-a-Phone – news · newspapers · books · scholar · JSTOR (November 2014) (Learn how and when to remove this message) DialaPhoneIndustryTelecommunicationsFounded1995FounderJonathan Beck and Richard FrankDefunct15 September 2014FateDefunct (ba...

Cet article est une ébauche concernant un club de football anglais. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations du projet football. Sheffield Wednesday Généralités Nom complet Sheffield Wednesday Football Club Surnoms The Owls[1] Noms précédents The Wednesday (jusqu'en 1929) Fondation 4 septembre 1867 Couleurs Bleu, blanc et noir Stade Hillsborough (39 732 places) Championnat actuel Championship (D2) Propriétaire Dejph...















